Эффективность

Существует несколько аспектов эффективности программ, включая такие наиболее общие, как время выполнения и требования по объему памяти. Другим аспектом является время, необходимое программисту для разработки программы.

Традиционная архитектура вычислительных машин не очень хорошо приспособлена для реализации прологовского способа выполнения программ, предусматривающего достижение целей из некоторого списка. Поэтому ограниченность ресурсов по времени и пространству сказывается в Прологе, пожалуй, в большей степени, чем в большинстве других языков программирования. Вызовет ли это трудности в практических приложениях, зависит от задачи. Фактор времени практически не имеет значения, если пролог-программа, которую запускают по несколько раз в день, занимает 1 секунду процессорного времени, а соответствующая программа на каком-либо другом языке, скажем на Фортране, - 0.1 секунды. Разница в эффективности становится существенной, если эти две программы требуют 50 и 5 минут соответственно.

С другой стороны, во многих областях применения Пролога он может существенно сократить время разработки программ. Программы на Прологе, вообще говоря, легче писать, легче понимать и отлаживать, чем программы, написанные на традиционных языках. Задачи, тяготеющие к "царству Пролога", включают в себя обработку символьной, нечисловой информации, структурированных объектов данных и отношений между ними. Пролог успешно применяется, в частности. в таких областях, как символьное решение уравнений, планирование, базы данных, автоматическое решение задач, машинное макетирование, реализация языков программирования, дискретное и аналоговое моделирование, архитектурное проектирование, машинное обучение, понимание естественного языка, экспертные системы и другие задачи искусственного интеллекта. С другой стороны, применение Пролога в области вычислительной математики вряд ли можно считать естественным.

Прогон откомпилированной программы обычно имеет большую эффективность, чем интерпретация. Поэтому, если пролог-система содержит как интерпретатор, так и компилятор, следует пользоваться компилятором, если время выполнения критично.

Если программа страдает неэффективностью, то ее обычно можно кардинально улучшить, изменив сам алгоритм. Однако для того, чтобы это сделать, необходимо изучить процедурные аспекты программы. Простой способ сокращения времени выполнения состоит в нахождении более удачного порядка предложений в процедуре и целей - в телах процедур. Другой, относительно простой метод заключается в управлении действиями системы посредством отсечений.

Полезные идеи, относящиеся к повышению эффективности, обычно возникают только при достижении более глубокого понимания задачи. Более эффективный алгоритм может, вообще говоря, привести к улучшениям двух видов: Повышение эффективности поиска путем скорейшего отказа от ненужного перебора и от вычисления бесполезных вариантов. Применение cтруктур данных, более приспособленных для представления объектов программы, с целью реализовать операции над ними более эффективно.

Мы изучим оба вида улучшений на примерах. Кроме того, мы рассмотрим на примере еще один метод повышения эффективности. Этот метод основан на добавлении в базу данных тех промежуточных результатов, которые с большой вероятностью могут потребоваться для дальнейших вычислений. Вместо того, чтобы вычислять их снова, программа просто отыщет их в базе данных как уже известные факты.

Повышение эффективности решения задачи о восьми ферзях
1. Повышение эффективности решения задачи о восьми ферзях

В качестве простого примера повышения эффективности давайте вернемся к задаче о восьми ферзях (см. рис. 4.7). В этой программе Y-координаты ферзей перебираются последовательно - для каждого ферзя пробуются числа от 1 до 8. Этот процесс был запрограммирован в виде цели

принадлежит( Y, [1, 2, 3, 4, 5, 6, 7, 8] )

Процедура принадлежит работает так: вначале пробует Y = 1, затем Y = 2, Y = 3 и т.д. Поскольку ферзи расположены один за другим в смежных вертикалях доски, очевидно, что такой порядок перебора не является оптимальным. Дело в том, что ферзи, расположенные в смежных вертикалях будут бить друг друга, если они не будут разнесены по вертикали на расстояние, превышающее, по крайней мере одно поле. В соответствии с этим наблюдением можно попытаться повысить эффективность, просто изменив порядок рассмотрения координат-кандидатов. Например:

принадлежит( Y, [1, 5, 2, 6, 3, 7, 4, 8] )

Это маленькое изменение уменьшит время, необходимое для нахождения первого решения, в 3-4 раза.

В следующем примере такая же простая идея, связанная с изменением порядка, превращает практически неприемлемую временную сложность в тривиальную.

Повышение эффективности программы раскраски карты
2. Повышение эффективности программы раскраски карты

Задача раскраски карты состоит в приписывании каждой стране на заданной карте одного из четырех заданных цветов с таким расчетом, чтобы ни одна пара соседних стран не была окрашена в одинаковый цвет. Существует теорема, которая гарантирует, что это всегда возможно.

Пусть карта задана отношением соседства

соседи( Страна, Соседи)

где Соседи - список стран, граничащих со страной Страна. При помощи этого отношения карта Европы с 20-ю странами будет представлена (в алфавитном порядке) так:

        соседи( австрия, [венгрия, запгермания, италия,
                                        лихтенштейн, чехословакия,
                                        швейцария, югославия]),

соседи( албания, [греция, югославия]).

соседи( андорра, [испания, франция]).

. . .

Решение представим в виде списка пар вида

Страна / Цвет

которые устанавливают цвет для каждой страны на данной карте. Для каждой карты названия стран всегда известны заранее, так что задача состоит в нахождении цветов. Таким образом, для Европы задача сводится к отысканию подходящей конкретизации переменных C1, C2, СЗ и т.д. в списке

[австрия/C1, албания/С2, андорра/С3, . . .]

Теперь определим предикат

цвета( СписЦветСтран)

который истинен, если СписЦветСтран удовлетворяет тем ограничениям, которые наложены на раскраску отношением соседи. Пусть четырьмя цветами будут желтый, синий, красный и зеленый. Условие запрета раскраски соседних стран в одинаковый цвет можно сформулировать на Прологе так:

цвета( [ ]).

        цвета( [Страна/Цвет | Остальные] ) :-
        цвета( Остальные),
            принадлежит( Цвет, [желтый, синий, красный, зеленый]),
            not( принадлежит( Страна1/Цвет, Остальные),
                                                        сосед( Страна, Страна1) ).

        сосед( Страна, Страна1) :-
                соседи( Страна, Соседи),
                принадлежит( Страна1, Соседи).

Здесь принадлежит( X, L) - как всегда, отношение принадлежности к списку. Для простых карт с небольшим числом стран такая программа будет работать. Что же касается Европы, то здесь результат проблематичен. Если считать, что мы располагаем встроенным предикатом setof, то можно попытаться раскрасить карту Европы следующим образом. Определим сначала вспомогательное отношение:

страна( С) :- соседи( С, _ ).

Тогда вопрос для раскраски карты Европы можно сформулировать так:

?- sеtоf( Стр/Цвет, страна( Стр), СписЦветСтран),
цвета( СписЦветСтран).

Цель setof - построить "шаблон" списка СписЦветСтран, в котором в элементах вида страна/ цвет вместо цветов будут стоять неконкретизированные переменные. Предполагается, что после этого цель цвета конкретизирует их. Такая попытка скорее всего потерпит неудачу вследствие неэффективности работы программы.

Тщательное исследование способа, при помощи которого пролог-система пытается достичь цели цвета, обнаруживает источник неэффективности. Страны расположены в списке в алфавитном порядке, а он не имеет никакого отношения к их географическим связям. Порядок, в котором странам приписываются цвета, соответствует порядку их расположения в списке (с конца к началу), что в нашем случае никак не связано с отношением соседи. Поэтому процесс раскраски начинается в одном конце карты, продолжается в другой и т.д., перемещаясь по ней более или менее случайно. Это легко может привести к ситуации, когда при попытке раскрасить очередную страну окажется, что она окружена странами, уже раскрашенными во все четыре доступных цвета. Подобные ситуации приводят к возвратам, снижающим эффективность.

Ясно поэтому, что эффективность зависит от порядка раскраски стран. Интуиция подсказывает простую стратегию раскраски, которая должна быть лучше, чем случайная: начать со страны, имеющей иного соседей, затем перейти к ее соседям, затем - к соседям соседей и т.д. В случае Европы хорошим кандидатом для начальной страны является Западная Германия (как имеющая наибольшее количество соседей - 9). Понятно, что при построении шаблона списка элементов вида страна/цвет Западную Германию следует поместить в конец этого списка, а остальные страны - добавлять со стороны его начала. Таким образом, алгоритм раскраски, который начинает работу с конца списка, в начале займется Западной Германией и продолжит работу, переходя от соседа к соседу.

Новый способ упорядочивания списка стран резко повышает эффективность по отношению к исходному, алфавитному порядку, и теперь возможные раскраски карты Европы будут получены без труда.

Можно было бы построить такой правильно упорядоченный список стран вручную, но в этом нет необходимости. Эту работу выполнит процедура создспис. Она начинает построение с некоторой указанной страны (в нашем случае - с Западной Германии) и собирает затем остальные страны в список под названием Закрытый. Каждая страна сначала попадает в другой список, названный Открытый, а потом переносится в Закрытый. Всякий раз, когда страна переносится из Открытый в Закрытый, ее соседи добавляются в Открытый.

        создспис( Спис) :-
                собрать( [запгермания], [ ], Спис ).
                собрать( [ ], Закрытый, Закрытый).
                                    % Кандидатов в Закрытый больше нет

        собрать( [X | Открытый], Закрытый, Спис) :-
                    принадлежит( Х | Закрытый), !,
                                        % Х уже собран ?

собрaть( Открытый, Закрытый, Спис).
% Отказаться от Х

        собрать( [X | Открытый], Закрытый, Спис) :-
                соседи( X, Соседи),
                                % Найти соседей Х
                конк( Соседи, Открытый, Открытый1),
                                % Поместить их в Открытый
                собрать( Открытый1, [X | Закрытый], Спис).
                                % Собрать остальные

Отношение конк - как всегда - отношение конкатенации списков.

Повышение эффективности конкатенации списков за счет совершенствования структуры данных
3. Повышение эффективности конкатенации списков за счет совершенствования структуры данных

До сих пор в наших программах конкатенация была определена так:

конк( [ ], L, L).

конк( [X | L1], L2, [X | L3] ) :-
конк( L1, L2, L3 ).

Эта процедура неэффективна, если первый список - длинный. Следующий пример объясняет, почему это так:

?- конк( [а, b, с], [d, e], L).

Этот вопрос порождает следующую последовательность целей:

конк( [а, b, с], [d, e], L)

конк( [b, с], [d, e], L') где L = [a | L']

конк( [с], [d, e], L") где L' = [b | L"]

конк( [ ], [d, e], L'") где L" = [c | L''']

true (истина) где L'" = [d, е]

Ясно, что программа фактически сканирует весь первый список, пока не обнаружит его конец.

А нельзя ли было бы проскочить весь первый список за один шаг и сразу подсоединить к нему второй список, вместо того, чтобы постепенно продвигаться вдоль него? Но для этого необходимо знать, где расположен конец списка, а следовательно, мы нуждаемся в другом его представлении. Один из вариантов - представлять список парой списков. Например, список

[а, b, с]

можно представить следующими двумя списками:

L1 = [a, b, c, d, e]
L2 = [d, e]

Подобная пара списков, записанная для краткости как L1-L2, представляет собой "разность" между L1 и L2. Это представление работает только при том условии, что L2 - "конечный участок" списка L1. Заметим, что один и тот же список может быть представлен несколькими "разностными парами". Поэтому список [а, b, с] можно представить как

        [а, b, с]-[ ]
или
        [a, b, c, d, e]-[d, e]
или
        [a, b, c, d, e | T]-[d, e | T]
или
        [а, b, с | Т]-Т

где Т - произвольный список, и т.п. Пустой список представляется любой парой L-L.

Поскольку второй член пары указывает на конец списка, этот конец доступен сразу. Это можно использовать для эффективной реализации конкатенации. Метод показан на рис. 8.1. Соответствующее отношение конкатенации записывается на Прологе в виде факта

конкат( A1-Z1, Z1-Z2, A1-Z2).

Давайте используем конкат для конкатенации двух списков: списка [а, b, с], представленного парой [а, b, с | Т1]-Т1, и списка [d, e], представленного парой [d, e | Т2]-Т2 :

?- конкат( [а, b, с | Т1]-T1, [d, е | Т2]-Т2, L ).

Оказывается, что для выполнения конкатенации достаточно простого сопоставления этой цели с предложением конкат. Результат сопоставления:

T1 = [d, e | Т2]
L = [a, b, c, d, e | T2]-T2

Стиль и методы программирования

Глава 8. СТИЛЬ И МЕТОДЫ ПРОГРАММИРОВАНИЯ

В этой главе мы рассмотрим некоторые общие принципы хорошего программирования и обсудим, в частности. следующие вопросы: "Как представлять себе прологовские программы? Из каких элементов складывается хороший стиль программирования на Прологе? Как отлаживать пролог - программы? Как повысить их эффективность ?"

double_line();

Как представлять себе программы на прологе

Как представлять себе программы на Прологе

Одной из характерных особенностей Пролога является то, что в нем допускается как процедурный, так и декларативный стиль мышления при составлении программы. Эти два подхода детально обсуждались в гл. 2 и затем многократно иллюстрировались на примерах. Какой из этих подходов окажется более эффективным и практичным, зависит от конкретной задачи. Обычно построение декларативного решения задачи требует меньших усилий, но может привести к неэффективной программе. В процессе построения решения мы должны сводить задачу к одной или нескольким более легким подзадачам. Возникает важный вопрос: как находить эти подзадачи? Существует несколько общих принципов, которые часто применяются при программировании на Прологе. Они будут обсуждаться в следующих разделах.

Использование рекурсии
1. Использование рекурсии

Этот принцип состоит в том, чтобы разбить задачу на случаи, относящиеся к двум группам:

(1) тривиальные, или "граничные" случаи;
(2) "общие" случаи, в которых решение получается из решений для (более простых) вариантов самой исходной задачи.

Этот метод мы использовали в Прологе постоянно. Рассмотрим еще один пример: обработка списка элементов, при которой каждый элемент преобразуется по одному и тому же правилу. Пусть это будет процедура

преобрспис( Спис, F, НовСпиc)

где Спис - исходный список, F - правило преобразования (бинарное отношение), а НовСпиc - список всех преобразованных элементов. Задачу преобразования списка Спис можно разбить на два случая:

(1) Граничный случай: Спис = [ ]

Если Спис = [ ], то НовСпиc = [ ], независимо от F

(2) Общий случай: Спис = [X | Хвост]

Чтобы преобразовать список вида [X | Хвост], необходимо:

                        преобразовать список Хвост; результат - НовХвост;
                        преобразовать элемент Х по правилу F; результат - НовХ;
                        результат преобразования всего списка - [НовХ | НовХвост].

Тот же алгоритм, изложенный на Прологе:

преобрспис( [ ], _, [ ]).

        преобрспис( [Х | Хвост], F, [НовХ | НовХвост] :-
                G =.. [F, X, НовХ],
                саll( G),
                пpeoбpcпиc( Хвост, F, НовХвост).

Одна из причин того, что рекурсия так естественна для определения отношений на Прологе, состоит в том, что объекты данных часто сами имеют рекурсивную структуру. К таким объектам относятся списки и деревья. Список либо пуст (граничный случай), либо имеет голову и хвост, который сам является списком (общий случай). Двоичное дерево либо пусто (граничный случай), либо у него есть корень и два поддерева, которые сами являются двоичными деревьями (общий случай). Поэтому для обработки всего непустого дерева необходимо сначала что-то сделать с его корнем, а затем обработать поддеревья.

Обобщение
2. Обобщение

Часто бывает полезно обобщить исходную задачу таким образом, чтобы полученная более общая задача допускала рекурсивную формулировку. Исходная задача решается, тогда как частный случай ее более общего варианта. Обобщение отношения обычно требует введения одного или более дополнительных аргументов. Главная проблема состоит в отыскании подходящего обобщения, что может потребовать более тщательного изучения задачи. В качестве примера рассмотрим еще раз задачу о восьми ферзях. Исходная задача состояла в следующем: разместить на доске восемь ферзей так, чтобы обеспечить отсутствие взаимных нападений. Соответствующее отношение назовем

восемьферзей( Поз)

Оно выполняется (истинно), если Поз - представленная тем или иным способом позиция, удовлетворяющая условию задачи. Можно предложить следующую полезную идею: обобщить задачу, перейдя от 8 ферзей к произвольному количеству - N. Количество ферзей станет дополнительным аргументом:

n_ферзей( Поз, N)

Преимущество такого обобщения состоит в том, что отношение n_ферзей допускает непосредственную рекурсивную формулировку:

(1) Граничный случай: N = 0
Разместить 0 ферзей - тривиальная задача.

(2) Общий случай: N > 0
Для "безопасного" размещения N ферзей необходимо:

получить требуемое размещение для (N - 1) ферзей и добавить оставшегося ферзя так, чтобы он не бил ни одного из уже поставленных ферзей.

Как только мы научимся решать более общую задачу, решить исходную уже не составит труда:

восемьферзей( Поз) :- n_ферзей( Поз, 8)

Использование рисунков
3. Использование рисунков

В поиске идей для решения задачи часто бывает полезным обратиться к ее графическому представлению. Рисунок может помочь выявить в задаче некоторые существенные отношения. После этого останется только описать на языке программирования то, что мы видим на рисунке.

Использование графического представления при решении задач полезно всегда, однако похоже, что в Прологе оно работает особенно хорошо. Происходит это по следующим причинам:

(1) Пролог особенно хорошо приспособлен для задач, в которых фигурируют объекты и отношения между ними. Часто такие задачи естественно иллюстрировать графами, в которых узлы соответствуют объектам, а дуги - отношениям.

(2) Естественным наглядным изображением структурных объектов Пролога являются деревья.

(3) Декларативный характер пролог-программ облегчает перевод графического представления на Пролог. В принципе, порядок описания "картинки" не играет роли, мы просто помещаем в программу то, что видим, в произвольном порядке. (Возможно, что из практических соображений этот порядок впоследствии придется подправить с целью повысить эффективность программы.)

Конкатенация списков, представленных в виде разностных пар.

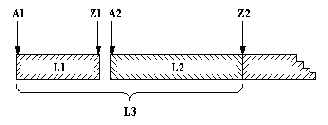
L1 представляется как A1-Z1, L2 как A2-Z2 и результат L3 - как A1-Z2.
При этом должно выполняться равенство Z1 = А2.

Повышение эффективности зa счет добавления вычисленных фактов к базе данных
4. Повышение эффективности зa счет добавления вычисленных фактов к базе данных

Иногда в процессе вычислений приходится одну и ту же цель достигать снова и снова. Поскольку в Прологе отсутствует специальный механизм выявления этой ситуации, соответствующая цепочка вычислений каждый раз повторяется заново.

В качестве примера рассмотрим программу вычисления N-го числа Фибоначчи для некоторого заданного N. Последовательность Фибоначчи имеет вид:

1, 1, 2, 3, 5, 8, 13, ...

Каждый член последовательности, за исключением первых двух, представляет собой сумму предыдущих двух членов. Для вычисления N-гo числа Фибоначчи F определим предикат

фиб( N, F)

Нумерацию чисел последовательности начнем с N = 1. Программа для фиб обрабатывает сначала первые два числа Фибоначчи как два особых случая, а затем определяет общее правило построения последовательности Фибоначчи:

фиб( 1, 1). % 1-е число Фибоначчи

фиб( 2, 1). % 2-е число Фибоначчи

        фиб( N, F) :-                         % N-е число Фиб., N > 2
                N > 2,
                N1 is N - 1, фиб( N1, F1),
                N2 is N - 2, фиб( N2, F2),
                F is F1 + F2.                % N-e число есть сумма двух
                                                    % предыдущих

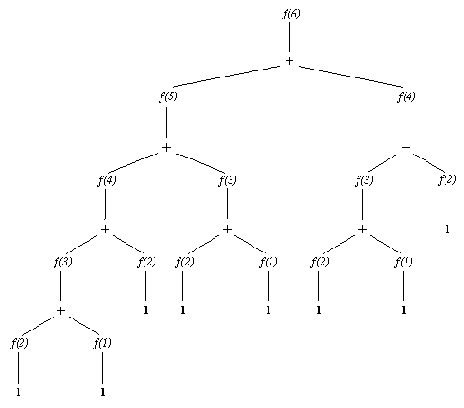
Процедура фиб имеет тенденцию к повторению вычислений. Это легко увидеть, если трассировать цель

?- фиб( 6, F).

На рис. 8.2 показано, как протекает этот вычислительный процесс. Например, третье число Фибоначчи f( 3) понадобилось в трех местах, и были повторены три раза одни и те же вычисления.

Этого легко избежать, если запоминать каждое вновь вычисленное число. Идея состоит в применении встроенной процедуры assert для добавления этих (промежуточных) результатов в базу данных в виде фактов. Эти факты должны предшествовать другим предложениям, чтобы предотвратить применение общего правила в случаях, для которых результат уже известен. Усовершенствованная процедура фиб2 отличается от фиб только этим добавлением:

фиб2( 1, 1). % 1-е число Фибоначчи

фиб2( 2, 1). % 2-е число Фибоначчи

        фиб2( N, F) :-                      % N-e число Фиб., N > 2
                N > 2,
                Nl is N - 1, фиб2( N1, F1),
                N2 is N - 2, фиб2( N2, F2),
                F is F1 + F2,                        % N-e число есть сумма
                                                            % двух предыдущих
                asserta( фиб2( N, F) ).      % Запоминание N-го числа

Эта программа, при попытке достичь какую-либо цель, будет смотреть сперва на накопленные об этом отношении факты и только после этого применять общее правило. В результате, после вычисления цели фиб2( N, F), все числа Фибоначчи вплоть до N-го будут сохранены. На рис. 8.3 показан процесс вычислении 6-го числа при помощи фиб2. Сравнение этого рисунка с рис. 8.2. показывает, на сколько уменьшилась вычислительная сложность. Для больших N такое уменьшение еще более ощутимо.

Запоминание промежуточных результатов - стандартный метод, позволяющий избегать повторных вычислений. Следует, однако, заметить, что в случае чисел Фибоначчи повторных вычислений можно избежать еще и применением другого алгоритма, а не только запоминанием промежуточных результатов.

Общие принципы хорошего программирования

Главный вопрос, касающийся хорошего программирования, - это вопрос о том, что такое хорошая программа. Ответ на этот вопрос не тривиален, поскольку существуют разные критерии качества программ.

Следующие критерии общеприняты: Правильность. Хорошая программа в первую очередь должна быть правильной, т. е. она должна делать именно то, для чего предназначалась. Это требование может показаться тривиальным и самоочевидным. Однако в случае сложных программ правильность достигается не так часто. Распространенной ошибкой при написании программ является пренебрежение этим очевидным критерием, когда большее внимание уделяется другим критериям - таким, как эффективность. Эффективность. Хорошая программа не должна попусту тратить компьютерное время и память. Простота, читабельность. Хорошая, программа должна быть легка для чтения и понимания. Она не должна быть более сложной, чем это необходимо. Следует избегать хитроумных программистских трюков, затемняющих смысл программы. Общая организация программы и расположение ее текста должны облегчать ее понимание. Удобство модификации. Хорошая программа должна быть легко модифицируема и расширяема. Простота и модульная организация программы облегчают внесение в нее изменений. Живучесть. Хорошая программа должна быть живучей. Она не должна сразу "ломаться", если пользователь введет в нее неправильные или непредусмотренные данные. В случае подобных ошибок программа должна сохранять работоспособность и вести себя разумно (сообщать об ошибках). Документированность. Хорошая программа должна быть хорошо документирована. Минимальная документация - листинг с достаточно подробными комментариями.

Степень важности того или иного критерия зависит от конкретной задачи, от обстоятельств написания программы, а также от условий ее эксплуатации. Наивысшим приоритетом пользуется, без сомнения, правильность. Обычно простоте, удобству модификации, живучести и документированности придают во крайней мере не меньший приоритет, чем эффективности.

Существует несколько общих соображений, помогающих реализовать вышеупомянутые критерии на практике. Одно важное правило состоит в том, чтобы сначала продумать задачу, подлежащую решению, и лишь затем приступать к написанию текста программы на конкретном языке программирования. Как только мы хорошо поймем задачу, и способ ее решения будет нами полностью и во всех деталях продуман, само программирование окажется быстрым и легким делом и появится неплохой шанс за короткое время получить правильную программу.

Распространенной ошибкой является попытка начать писать программу даже до того, как была уяснена полная постановка задачи. Главная причина, по которой следует воздерживаться от преждевременного начала программирования, состоит в том, что обдумывание задачи и поиск метода ее решения должны проводиться в терминах, наиболее адекватных самой этой задаче. Эти термины чаще всего далеки от синтаксиса применяемого языка программирования и могут быть утверждениями на естественном языке и рисунками.

Исходная формулировка способа решения задачи должна быть затем трансформирована в программу, но этот процесс трансформации может оказаться нелегким. Неплохим подходом к его осуществлению является применение принципа пошаговой детализации. Исходная формулировка рассматривается как "решение верхнего уровня", а окончательная программа - как "решение низшего уровня".

В соответствии с принципом пошаговой детализации окончательная программа получается после серии трансформаций или "детализаций" решения. Мы начинаем с первого решения - решения верхнего уровня, а затем последовательно проходим по цепочке решений; все эти решения эквивалентны, но каждое следующее решение выражено более детально, чей предыдущее. На каждом шагу детализации понятия, использовавшиеся в предыдущих формулировках, прорабатываются более подробно, а их представление все более приближается к языку программирования. Следует отдавать себе отчет в том, что детализация касается не только процедур, но и структур данных. На начальных шагах работают обычно с более абстрактными, более крупными информационными единицами, детальная структура которых уточняется впоследствии.

Стратегия нисходящей пошаговой детализации имеет следующие преимущества: она позволяет сформулировать грубое решение в терминах, наиболее адекватных решаемой задаче; в терминах таких мощных понятий решение будет сжатым и простым, а потому скорее всего правильным; каждый шаг детализации должен быть достаточно малым, чтобы не представлять больших интеллектуальных трудностей, если это удалось - трансформация решения в новое, более детальное представление скорее всего будет выполнена правильно, а следовательно, таким же правильным окажется и полученное решение следующего шага детализации.

В случае Пролога мы можем говорить о пошаговой детализации отношений. Если существо задачи требует мышления в алгоритмических терминах, то мы можем также говорить и о детализации алгоритмов, приняв процедурную точку зрения на Пролог.

Для того, чтобы удачно сформулировать решение на некотором уровне детализации и придумать полезные понятия для следующего, более низкого уровня, нужны идеи. Поэтому программирование - это творческий процесс, что верно в особенности, когда речь идет о начинающих программистах. По мере накопления опыта работа программиста постепенно становится все менее искусством и все более ремеслом. И все же главным остается вопрос: как возникают идеи? Большинство идей приходит из опыта, из тех задач, решения которых уже известны. Если мы не знаем прямого решения задачи, то нам может помочь уже решенная задача, похожая на нашу. Другим источником идей является повседневная жизнь. Например, если необходимо запрограммировать сортировку списка, то можно догадаться, как это сделать, если задать себе вопрос: "А как бы я сам стал действовать, чтобы расположить экзаменационные листы студентов по их фамилиям в алфавитном порядке?"

Общие принципы, изложенные в данном разделе, известны также как составные части "структурного программирования"; они, в основном, применимы и к программированию на Прологе. В следующих разделах мы обсудим их более детально, обращая особое внимание на применение этих принципов программирования к Прологу.

Отладка

Когда программа не делает того, чего от нее ждут, главной проблемой становится отыскание ошибки (или ошибок). Всегда легче найти ошибку в какой-нибудь части программы (или в отдельном модуле), чем во всей программе. Поэтому следует придерживаться следующего хорошего принципа: проверять сначала более мелкие программные единицы и только после того, как вы убедились, что им можно доверять, начинать проверку большего модуля или всей программы.

Отладка в Прологе облегчается двумя обстоятельствами: во-первых, Пролог - интерактивный язык, поэтому можно непосредственно обратиться к любой части программы, задав пролог-системе соответствующий вопрос; во-вторых, в реализациях Пролога обычно имеются специальные средства отладки. Следствием этих двух обстоятельств является то, что отладка программ на Прологе может производиться, вообще говоря, значительно эффективнее, чем в других языках программирования.

Основным средством отладки является трассировка (tracing). "Трассировать цель" означает: предоставить пользователю информацию, относящуюся к достижению этой цели в процессе ее обработки пролог-системой. Эта информация включает: Входную информацию - имя предиката и значении аргументов в момент активизации цели. Выходную информацию - в случае успеха, значения аргументов, удовлетворяющих цели; в противном случае - сообщение о неуспехе. Информацию о повторном входе, т. е. об активизации той же цели в результате автоматического возврата.

В промежутке между входом и выходом можно получить трассировочную информацию для всех подцелей этой цели. Таким образом, мы можем следить за обработкой нашего вопроса на всем протяжении нисходящего пути от исходной цели к целям самого нижнего уровня, вплоть до отдельных фактов. Такая детальная трассировка может оказаться непрактичной из-за непомерно большого количества трассировочной информации. Поэтому пользователь может применить "селективную" трассировку. Существуют два механизма селекции: первый подавляет выдачу информации о целях, расположенных ниже некоторого уровня; второй трассирует не все предикаты, а только некоторые, указанные пользователем.

Средства отладки приводятся в действие при помощи системно-зависимых встроенных предикатов. Обычно используется следующий стандартный набор таких предикатов:

trace

запускает полную трассировку всех целей, следующих за trace.

notrace

прекращает дальнейшее трассирование .

spy( P) (следи за Р)

устанавливает режим трассировки предиката Р. Обращение к spy применяют, когда хотят получить информацию только об указанном предикате и избежать трассировочной информации от других целей (как выше, так и ниже уровня запуска Р). "Следить" можно сразу за несколькими предикатами .

nospy( Р)

прекращает "слежку" за Р.

Трассировка ниже определенной глубины может быть подавлена во время выполнения программы при помощи специальных команд. Существуют и другие команды отладки, такие как возврат к предыдущей точке процесса вычислений. После такого возврата можно, например, повторить вычисления с большей степенью детализации трассировки.

Отношения в последовательности фибоначчи. "конфигурация" изображается

Отношения в последовательности Фибоначчи. "Конфигурация" изображается

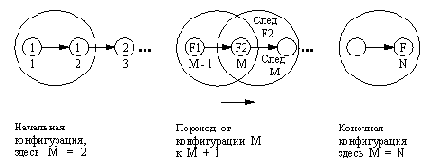
здесь в виде большого круга и определяется тремя параметрами: индексом М и двумя
последовательными числами f( M-1) и f( М).

Для оценки качества программы существует

Резюме

Для оценки качества программы существует несколько критериев:

        правильность
        эффективность
        простота, читабельность
        удобство модификации
        документированность
Принцип пошаговой детализации - хороший способ организации процесса разработки программ. Пошаговая детализация применима к отношениям, алгоритмам и структурам данных. Следующие методы часто помогают находить идеи для совершенствования программ на Прологе:

Применение рекурсии: выявить граничные и общие случаи рекурсивного определения.

Обобщение: рассмотреть такую более общую задачу, которую проще решить, чем исходную.

Использование рисунков: графическое представление помогает в выявлении важных отношений.
Полезно следовать некоторым стилистическим соглашениям для уменьшения опасности внесения ошибок в программы и создания программ, легких для чтения, отладки и модификации. В пролог-системах обычно имеются средства отладки. Наиболее полезными являются средства трассировки программ. Существует много способов повышения эффективности программы. Наиболее простые способы включают в себя:

изменение порядка целей и предложений

управляемый перебор при помощи введения отсечений

запоминание (с помощью assert) решений, которые иначе пришлось бы перевычислять Более тонкие и радикальные методы связаны с улучшением алгоритмов (особенно, в части повышения эффективности перебора) и с совершенствованием структур данных.

Стиль программирования

Подчиняться при программировании некоторым стилистическим соглашениям нужно для того, чтобы уменьшить опасность внесения ошибок в программы и создавать программы, которые легко читать, понимать, отлаживать и модифицировать.

Ниже дается обзор некоторых из составных частей хорошего стиля программирования на Прологе. Мы рассмотрим некоторые общие правила хорошего стиля, табличную организацию длинных процедур и вопросы комментирования программ.

    Некоторые правила хорошего стиля
1.    Некоторые правила хорошего стиля

Предложения программы должны быть короткими. Их тела, как правило, должны содержать только несколько целей. Процедуры должны быть короткими, поскольку длинные процедуры трудны для понимания. Тем не менее длинные процедуры вполне допустимы в том случае, когда они имеют регулярную структуру (этот вопрос еще будет обсуждаться в данной главе). Следует применять мнемонические имена процедур и переменных. Они должны отражать смысл отношений и роль объектов данных. Существенное значение имеет расположение текста программы. Для улучшения читабельности программы нужно постоянно применять пробелы, пустые строки и отступы. Предложения, относящиеся к одной процедуре, следует размещать вместе в виде отдельной группы строк; между предложениями нужно вставлять пустую строку (этого не нужно делать, возможно, только в случае перечисления большого количества фактов, касающихся одного отношения); каждую цель можно размещать на отдельной строке. Пролог-программы иной раз напоминают стихи по эстетической привлекательности своих идей и формы. Стилистические соглашения такого рода могут варьироваться от программы к программе, так как они зависят от задачи и от личного вкуса. Важно, однако, чтобы на протяжении одной программы постоянно применялись одни и те же соглашения. Оператор отсечения следует применять с осторожностью. Если легко можно обойтись без него - не пользуйтесь им. Всегда, когда это возможно, предпочтение следует отдавать "зеленым отсечениям" перед "красными". Как говорилось в гл. 5, отсечение называется "зеленым", если его можно убрать, на затрагивая декларативный смысл предложения. Использование "красных отсечений" должно ограничиваться четко определенными конструкциями, такими как оператор not или конструкция выбора между альтернативами. Примером последней может служить

        если Условие то Цель1 иначе Цель2

С использованием отсечения эта конструкция переводится на Пролог так:

        Условие, !.             % Условие выполнено?

        Цель1;                     % Если да, то Цель1

        Цель2                      % Иначе - Цель2
Из-за того, что оператор not связан с отсечением, он тоже может привести к неожиданностям. Поэтому, применяя его, следует всегда помнить точное прологовское определение этого оператора. Тем не менее, если приходится выбирать между not и отсечением, то лучше использовать not, чем какую-нибудь туманную конструкцию с отсечением. Внесение изменений в программу при помощи assert и retract может сделать поведение программы значительно менее понятным. В частности, одна и та же программа на одни н те же вопросы будет отвечать по-разному в разные моменты времени. В таких случаях, если мы захотим повторно воспроизвести исходное поведение программы, нам придется предварительно убедиться в том, что ее исходное состояние, нарушенное при обращении к assert и retract, полностью восстановлено. Применение точек с запятой может затемнять смысл предложений. Читабельность можно иногда улучшить, разбивая предложения, содержащие точки с запятой, на несколько новых предложений, однако за это, возможно, придется заплатить увеличенном длины программы и потерей в ее эффективности.

Для иллюстрации некоторых положений данного раздела рассмотрим отношение

слить( Спис1, Спис2, Спис3)

где Спис1 и Спис2 - упорядоченные списки, а Спис3 -результат их слияния (тоже упорядоченный). Например:

слить( [2, 4, 7], [1, 3, 4, 8], [1, 2, 3, 4, 4, 7, 8] )

Вот стилистически неудачная реализация этого отношения:

        слить( Спис1, Спис2, Спис3) :-
                Спис1 = [ ], !, Спис3 = Спис2;
                                                    % Первый список пуст
                Спис2 = [ ], !, Спис3 = Спис1;
                                                    % Второй список пуст
                Спис1 = [X | Остальные],
                Спис2 = [Y | Остальные],
                ( Х < Y, !,
                Z = X,                           % Z - голова Спис3
                слить( Остальные1, Спис2, Остальные3 );
                Z = Y,
                слить( Спис1, Остальные2, Остальные3 ) ),
                Спис3 = [Z | Остальные3].

Вот более предпочтительный вариант, не использующий точек с запятой:

слить( [ ], Спис, Спис).

слить( Спис, [ ], Спис).

                слить( [X | Остальные1], [Y | Остальные2], [X | Остальные3] ) :-
                Х < Y, !,
                слить(Остальные1, [Y | Остальные2], Остальные3).

слить( Спис1, [Y | Остальные2], [Y | Остальные3]): -
слить( Спис1, Остальные2, Остальные3 ).

Табличная организация длинных процедур
2. Табличная организация длинных процедур

Длинные процедуры допустимы, если они имеют регулярную структуру. Обычно эта структура представляет собой множество фактов, соответствующее определению какого-либо отношения в табличной форме. Преимущества такой организации длинной процедуры состоят в том, что: Ее структуру легко понять. Ее удобно совершенствовать: улучшать ее можно, просто добавляя новые факты. Ее легко проверять и модифицировать (просто заменяя отдельные факты, независимо от остальных).

3. Комментирование

Программные комментарии должны объяснять в первую очередь, для чего программа предназначена и как ею пользоваться, и только затем - подробности используемого метода решения и другие программные детали. Главная цель комментариев - обеспечить пользователю возможность применять программу, понимать ее и, может быть, модифицировать. Комментарии должны содержать в наиболее краткой форме всю необходимую для этого информацию. Недостаточное комментирование - распространенная ошибка, однако, программу можно и перенасытить комментариями. Объяснения деталей, которые и так ясны из самого текста программы, являются ненужной перегрузкой.

Длинные фрагменты комментариев следует располагать перед текстом, к которому они относятся, в то время как короткие комментарии должны быть вкраплены в сам текст. Информация, которую в самом общем случае следует включать в комментарии, должна схватывать следующие вопросы: Что программа делает, как ею пользоваться (например, какую цель следует активизировать и каков вид ожидаемых результатов), примеры ее применения. Какие предикаты относятся к верхнему уровню? Как представлены основные понятия (объекты)? Время выполнения и требования по объему памяти. Каковы ограничения на программу? Использует ли она какие-либо средства, связанные с конкретной операционной системой? Каков смысл предикатов программы? Каковы их аргументы? Какие аргументы являются "входными" и какие - "выходными", если это известно? (В момент запуска предиката входные аргументы имеют полностью определенные значения, не содержащие не конкретизированных переменных.) Алгоритмические и реализационные детали.

Все показанные ниже процедуры подсп1,

Упражнения

Все показанные ниже процедуры подсп1, подсп2 и подсп3 реализуют отношение взятия подсписка. Отношение подсп1 имеет в значительной мере процедурное определение, тогда как подсп2 и подсп3 написаны в декларативном стиле. Изучите поведение этих процедур на примерах нескольких списков, обращая внимание на эффективность работы. Две из них ведут себя одинаково и имеют одинаковую эффективность. Какие? Почему оставшаяся процедура менее эффективна?
        подсп1( Спис, Подспис) :-
                начало( Спис, Подспис).
        подсп1( [ _ | Хвост], Подспис) :-
                                                % Подспис - подсписок хвоста
                подсп1( Хвост, Подспис).
        начало( _, [ ]).
        начало( [X | Спис1], [X | Спис2] ) :-
                начало( Спис1, Спис2).
        подсп2( Спис, Подспис) :-
                конк( Спис1, Спис2, Спис),
                конк( Спис3, Подспис, Cпис1).
        подсп3( Спис, Подспис) :-
                конк( Спис1, Спис2, Спис),
                конк( Подспис, _, Спис2).
    Определите отношение
        добавить_в_конец( Список, Элемент, НовыйСписок)
добавляющее Элемент в конец списка Список; результат - НовыйСписок. Оба списка представляйте разностными парами.
Посмотреть ответ
    Определите отношение
        обратить( Список, ОбращенныйСписок)
где оба списка представлены разностными парами.
Посмотреть ответ
    Перепищите процедуру собрать из разд. 8.5.2, используя разностное представление списков, чтобы конкатенация выполнялась эффективнее.

Вычисление 6-го числа фибоначчи...

Вычисление 6-го числа Фибоначчи при помощи процедуры фиб2, которая запоминает предыдущие результаты. По сравнению с процедурой фиб здесь вычислений меньше (см. рис. 8.2).

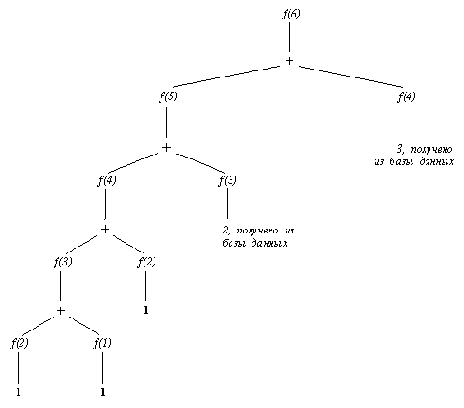
Этот новый алгоритм позволяет создать программу более трудную для понимания, зато более эффективную. Идея состоит на этот раз не в том, чтобы определить N-e число Фибоначчи просто как сумму своих предшественников по последовательности, оставляя рекурсивным вызовам организовать вычисления "сверху вниз" вплоть до самых первых двух чисел. Вместо этого можно работать "снизу вверх": начать с первых двух чисел и продвигаться вперед, вычисляя члены последовательности один за другим. Остановиться нужно в тот момент, когда будет достигнуто N-e число. Большая часть работы в такой программе выполняется процедурой

фибвперед( М, N, F1, F2, F)

Здесь F1 и F2 - (М - 1)-е и М-е числа, а F - N-e число Фибоначчи. Рис. 8.4 помогает понять отношение фибвперед. В соответствии с этим рисунком фибвперед находит последовательность преобразований для достижения конечной конфигурации (в которой М = N) из некоторой заданной начальной конфигурации. При запуске фибвперед все его аргументы, кроме F, должны быть конкретизированы, а М должно быть меньше или равно N. Вот эта программа:

        фиб3( N, F) :-
                фибвперед( 2, N, 1, 1, F).
                                    % Первые два числа Фиб. равны 1

фибвперед( М, N, F1, F2, F2) :-
М >= N. % N-e число достигнуто

        фибвперед( M, N, F1, F2, F) :-
                M < N,       % N-e число еще не достигнуто
                СледМ is М + 1,
                СледF2 is F1 + F2,
                фибвперед( СледМ, N, F2, СледF2, F).

Вычисление 6-го числа фибоначчи процедурой фиб.

Вычисление 6-го числа Фибоначчи процедурой фиб.