Предварительные понятия и примеры
Рассмотрим пример, представленный на рис. 11.1. Задача состоит в выработке плана переупорядочивания кубиков, поставленных друг на друга, как показано на рисунке. На каждом шагу разрешается переставлять только один кубик. Кубик можно взять только тогда, когда его верхняя поверхность свободна. Кубик можно поставить либо на стол, либо на другой кубик. Для того, чтобы построить требуемый план, мы должны отыскать последовательность ходов, реализующую заданную трансформацию.
Эту задачу можно представлять себе как задачу выбора среди множества возможных альтернатив. В исходной ситуации альтернатива всего одна: поставить кубик С на стол. После того как кубик С поставлен на стол, мы имеем три альтернативы: поставить А на стол или поставить А на С, или поставить С на А.

Рис. 11. 1. Задача перестановки кубиков.
Ясно, что альтернативу "поставить С на стол" не имело смысла рассматривать всерьез, так как этот ход никак не влияет на ситуацию.
Как показывает рассмотренный пример, с задачами такого рода связано два типа понятий:
(1) Проблемные ситуации.
(2) Разрешенные ходы или действия, преобразующие одни проблемные ситуации в другие.
Проблемные ситуации вместе с возможными ходами образуют направленный граф, называемый пространством состояний. Пространство состояний для только что рассмотренного примера дано на рис. 11.2. Вершины графа соответствуют проблемным ситуациям, дуги - разрешенным переходам из одних состояний в другие. Задача отыскания плана решения задачи эквивалентна задаче построения пути между заданной начальной ситуацией ("стартовой" вершиной) и некоторой указанной заранее конечной ситуацией, называемой также целевой вершиной.
На рис. 11.3 показан еще один пример задачи: головоломка "игра в восемь" в ее представление в виде задачи поиска пути. В головоломке используется восемь перемещаемых фишек, пронумерованных цифрами от 1 до 8. Фишки располагаются в девяти ячейках, образующих матрицу 3 на 3.
Одна из ячеек

Рис. 11. 2. Графическое представление задачи манипулирования
кубиками. Выделенный путь является решением задачи рис. 11.1.
всегда пуста, и любая смежная с ней фишка может быть передвинута в эту пустую ячейку. Можно сказать и по-другому, что пустой ячейке разрешается перемещаться, меняясь местами с любой из смежных с ней фишек. Конечная ситуация - это некоторая заранее заданная конфигурация фишек, как показано на рис. 11.3.
Нетрудно построить аналогичное представление в виде графа и для других популярных головоломок. Наиболее очевидные примеры - это задача о "ханойской башне" и задача о перевозке через реку волка, козы и капусты. Во второй из этих задач предполагается, что вместе с человекам в лодке помещается только один объект и что человеку приходится охра-
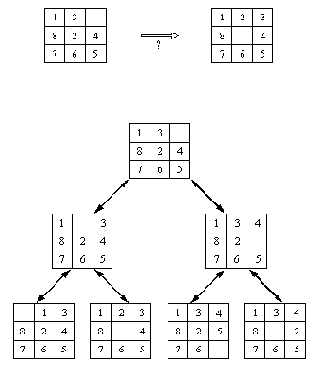
Рис. 11. 3. "Игра в восемь" и ее представление в форме графа.
нять козу от волка и капусту от козы. С описанной парадигмой согласуются также многие задачи, имеющие практическое значение. Среди них - задача о коммивояжере, которая может служить моделью для многих практических оптимизационных задач. В задаче дается карта с n городами в указываются расстояния, которые надо преодолеть по дорогам при переезде из города в город. Необходимо найти маршрут, начинающийся в некотором городе, проходящий через все города и заканчивающиеся в том же городе. Ни один город, за исключением начального, не разрешается посещать дважды.
Давайте подытожим те понятия, которые мы ввели, рассматривая примеры. Пространство состояний некоторой задачи определяет "правила игры": вершины пространства состояния соответствуют ситуациям, а дуги - разрешенным ходам или действиям, или шагам решения задачи. Конкретная задача определяется пространством состояний стартовой вершиной целевым условием (т.е. условием, к достижению которого следует стремиться); "целевые вершины" - это вершины, удовлетворяющие этим условиям. Каждому разрешенному ходу или действию можно приписать его стоимость.
Например, в задаче манипуляции кубиками стоимости, приписанные тем или иным перемещениям кубиков, будут указывать иам на то, что некоторые кубики перемещать труднее, чем другие. В задаче о коммивояжере ходы соответствуют переездам из города в город. Ясно, что в данном случае стоимость хода - это расстояние между соответствующими городами.
В тех случаях, когда каждый ход имеет стоимость, мы заинтересованы в отыскании решения минимальной стоимости. Стоимость решения - это сумма стоимостей дуг, из которых состоит "решающий путь" - путь из стартовой вершины в целевую. Даже если стоимости не заданы, все равно может возникнуть оптимизационная задача: нас может интересовать кратчайшее решение.
Прежде тем будут рассмотрены некоторые программы, реализующие классический алгоритм поиска в пространстве состоянии, давайте сначала обсудим. как пространство состояний может быть представлено в прологовской программе.
Мы будем представлять пространство состояний при помощи отношения
после( X, Y)
которое истинно тогда, когда в пространстве состояний существует разрешенный ход из вершины Х в вершину Y. Будем говорить, что Y - это преемник вершины X. Если с ходами связаны их стоимости, мы добавим третий аргумент, стоимость хода:
после( X, Y, Ст)
Эти отношения можно задавать в программе явным образом при помощи набора соответствующих фактов. Однако такой принцип оказывается непрактичным и нереальным для тех типичных случаев, когда пространство состояний устроено достаточно сложно. Поэтому отношение следования после обычно определяется неявно, при помощи правил вычисления вершин-преемников некоторой заданной вершины. Другим вопросом, представляющим интерес с самой общей точки зрения, является вопрос о способе представления состояний, т.е. самих вершин. Это представление должно быть компактным, но в то же время оно должно обеспечивать эффективное выполнение необходимых операций, в частности операции вычисления вершин-преемников, а возможно и стоимостей соответствующих ходов.
Рассмотрим в качестве примера задачу манипулирования кубиками, проиллюстрированную на рис. 11.1. Мы будем рассматривать более общий случай, когда имеется произвольное число кубиков, из которых составлены столбики, - один или несколько. Число столбиков мы ограничим некоторым максимальным числом, чтобы задача была интереснее. Такое ограничение, кроме того, является вполне реальным, поскольку рабочее пространство, которым располагает робот, манипулирующий - кубиками, ограничено.
Проблемную ситуацию можно представить как список столбиков. Каждый столбик в свою очередь представляется списком кубиков, из которых он составлен. Кубики упорядочены в списке таким образом, что самый верхний кубик находится в голове списка. "Пустые" столбики изображаются как пустые списки. Таким образом, исходную ситуацию рис. 11.1 можно записать как терм
[ [с, а, b], [ ], [ ] ]
Целевая ситуация - это любая конфигурация кубиков, содержащая, столбик, составленный из всех имеющихся кубиков в указанном порядке. Таких ситуаций три:
[ [a, b, c], [ ], [ ] ]
[ [ ], [а, b, с], [ ] ]
[ [ ], [ ], [a, b, c] ]
Отношение следования можно запрограммировать, исходя из следующего правила: ситуация Сит2 есть преемник ситуации Сит1, если в Сит1 имеется два столбика Столб1 и Столб2, такие, что верхний кубик из Столб1 можно поставить сверху на Столб2 и получить тем самым Сит2. Поскольку все ситуации - это списки столбиков, правило транслируется на Пролог так:
после( Столбы, [Столб1, [Верх1 | Столб2], Остальные]) :-
% Переставить Верх1 на Столб2
удалить( [Верх1 | Столб1], Столб1, Столб1),
% Найти первый столбик
удалить( Столб2, Столбы1, Остальные).
% Найти второй столбик
удалить( X, [X | L], L).
удалить( X, [Y | L], [Y | L1] ) :-
удалить( L, X, L1).
В нашем примере целевое условие имеет вид:
цель( Ситуация) :-
принадлежит [а,b,с], Ситуация)
Алгоритм поиска мы запрограммируем как отношение
решить( Старт, Решение)
где Старт - стартовая вершина пространства состояний, а Решение - путь, ведущий из вершины Старт в любую целевую вершину. Для нашего конкретного примера обращение к пролог-системе имеет вид:
?- решить( [ [с, а, b], [ ], [ ] ], Решение).
В результате успешного поиска переменная Решение конкретизируется и превращается в список конфигураций кубиков. Этот список представляет собой план преобразования исходного состояния в состояние, в котором все три кубика поставлены друг на друга в указанном порядке [а, b, с].
Назад | Содержание | Вперёд
Применение поиска с предпочтением к планированию выполнения задач
Рассмотрим следующую задачу планирования. Дана совокупность задач t1, t2, ..., имеющих времена выполнения соответственно T1, Т2, ... . Все эти задачи нужно решить на m идентичных процессорах. Каждая задача может быть решена на любом процессоре, но в каждый данный момент каждый процессор решает только одну из задач. Между задачами существует отношение предшествования, определяющее, какие задачи (если таковые есть) должны быть завершены, прежде чем данная задача может быть запущена. Необходимо распределить задачи между процессорами без нарушения отношения предшествования, причем таким образом, чтобы вся совокупность задач была решена за минимальное время. Время, когда последняя задача в соответствии с выработанным планом завершает свое решение, называется временем окончания плана. Мы хотим минимизировать время окончания по всем возможным планам.
На рис. 12.8 показан пример задачи планирования, а также приведено два корректных плана, один из которых оптимален. Из примера видно, что оптимальный план обладает одним интересным свойством, а именно в нем может предусматриваться "время простоя" процессоров. В оптимальном плане рис. 12.8 процессор 1, выполнив задачу t, ждет в течение двух квантов времени, несмотря на то, что он мог бы начать выполнение задачи t.
Один из способов построить план можно грубо сформулировать так. Начинаем с пустого плана (с незаполненными временными промежутками для каждого процессора) и постепенно включаем в него задачи

Рис. 12. 8. Планирование прохождения задач в многопроцессорной системе для 7 задач и 3 процессоров. Вверху показано предшествование задач и величины продолжительности их решения. Например, задача t5 требует 20 квантов времени, причем ее выполнение может начаться только после того, как будет завершено решение трех других задач t1, t2 и t3. Показано два корректных плана: оптимальный план с временем окончания 24 и субоптимальный - с временем окончания 33. В данной задаче любой оптимальный план должен содержать время простоя.
Coffman/ Denning, Operating Systems Theory, © 1973, p.86. Приведено с разрешения Prentice-Hall, Englewood Cliffs, New Jersey.
одну за другой, пока все задачи не будут исчерпаны. Как правило, на каждом шагу мы будем иметь несколько различных возможностей, поскольку окажется, что одновременно несколько задач-кандидатов ждут своего выполнения. Таким образом, для составления плана потребуется перебор. Мы можем сформулировать задачу планирования в терминах пространства состояний следующим образом:
состояния - это частично составленные планы;
преемник частичного плана получается включением в план еще одной задачи; другая возможность - оставить процессор, только что закончивший свою задачу, в состоянии простоя;
стартовая вершина - пустой план;
любой план, содержащий все задачи, - целевое состояние;
стоимость решения (подлежащая минимизации) -время окончания целевого плана;
стоимость перехода от одного частичного плана к другому равна К2 - К1 где К1, К2 - времена окончания этих планов.
Этот грубый сценарий требует некоторых уточнений. Во-первых, мы решим заполнять план в порядке возрастания времен, так что задачи будут включаться в него слева направо. Кроме того, при добавлении каждой задачи следует проверять, выполнены ли ограничения, связанные с отношениями предшествования. Далее, не имеет смысла оставлять процессор бездействующим на неопределенное время, если имеются задачи, ждущие своего запуска. Поэтому мы разрешим процессору простаивать только до того момента, когда какой-нибудь другой процессор завершит выполнение своей задачи. В этот момент мы еще раз вернемся к свободному процессору с тем, чтобы рассмотреть возможность приписывания ему какой-нибудь задачи.
Теперь нам необходимо принять решение относительно представления проблемных ситуаций, т.е. частичных планов. Нам понадобится следующая информация:
(1) список ждущих задач вместе с их временами выполнения;
(2) текущая загрузка процессоров задачами.
Добавим также для удобства программирования
(3) время окончания (частичного) плана, т.е. самое последнее время окончания задачи среди всех задач, приписанных процессорам.
Список ждущих задач вместе с временами их выполнения будем представлять в программе при помощи списка вида
[ Задача1/Т1, Задача2/Т2, ... ]
Текущую загрузку процессоров будем представлять как список решаемых задач, т. е. список пар вида
[ Задача/ВремяОкончания ]
В списке m таких пар, по одной на каждый процессор. Новая задача будет добавляться к плану в момент, когда закончится первая задача из этого списка. В связи с этим мы должны постоянно поддерживать упорядоченность списка загрузки по возрастанию времен окончания. Эти три компоненты частичного плана (ждущие задачи, текущая загрузка и время окончания плана) будут объединены в одно выражение вида
Ждущие * Активные * ВремяОкончания
Кроме этой информации у нас есть ограничения, налагаемые отношениями предшествования, которые в программе будут выражены в форме отношения
предш( ЗадачаX, ЗадачаY)
Рассмотрим теперь эвристическую оценку. Мы будем использовать довольно примитивную эвристическую функцию, которая не сможет обеспечить высокую эффективность управления алгоритмом поиска. Эта функция допустима, так что получение оптимального плана будет гарантировано. Однако следует заметить, что для решения более серьезных задач планирования потребуется более мощная эвристика.
Нашей эвристической функцией будет оптимистическая оценка времени окончания частичного плана с учетом всех ждущих задач. Оптимистическая оценка будет вычисляться в предположении, что два из ограничений, налагаемых на действительно корректный план, ослаблены:
(1) не учитываются отношения предшествования;
(2) делается (не реальное) допущение, что возможно распределенное выполнение задачи одновременно на нескольких процессорах, причем сумма времен выполнения задачи на процессорах равна исходному времени выполнения этой задачи на одном процессоре.
Пусть времена выполнения ждущих задач равны Т1, Т2, ..., а времена окончания задач, выполняемых на процессорах - К1, К2, ... . Тогда оптимистическая оценка времени ОбщКон окончания всех активных к настоящему моменту, а также всех ждущих задач имеет вид:

где m - число процессоров. Пусть время окончания текущего частичного плана равно
Кон = maх(Kj).
j
Тогда эвристическая оценка Н (дополнительное время для включения в частичный план ждущих задач) определяется следующим выражением:
if ОбщКон>Кон then Н = ОбщКон-Кон else H=0
Программа, содержащая определения отношений, связанных с пространством состояний нашей задачи планирования, приведена полностью на рис. 12.9. Эта программа включает в себя также спецификацию конкретной задачи планирования, показанной на рис. 12.3. Одно из оптимальных решений, полученных в процессе поиска с предпочтением в определенном таким образом пространстве состояний, показано на рис. 12.8.
обезьяна и банан
Задача об обезьяне и банане часто используется в качестве простого примера задачи из области искуственного интеллекта. Наша пролог-программа, способная ее решить, показывает, как механизмы сопоставления и автоматических возвратов могут применяться для подобных целей. Мы сначала составим программу, не принимая во внимание процедурную семантику, а затем детально изучим ее процедурное поведение. Программа будет компактной и наглядной.
Рассмотрим следующий вариант данной задачи. Возле двери комнаты стоит обезьяна. В середине этой комнаты к потолку подвешен банан. Обезьяна голодна и хочет съесть банан, однако она не может дотянуться до него, находясь на полу. Около окна этой же комнаты на полу лежит ящик, которым обезьяна может воспользоваться. Обезьяна может предпринимать следующие действия: ходить по полу, залезать на ящик, двигать ящик (если она уже находится около него) и схватить банан, если она стоит на ящике прямо под бананом. Может ли обезьяна добраться до банана?
Одна из важных проблем при программировании состоит в выборе (адекватного) представления решаемой задачи в терминах понятий используемого языка программирования. В нашем случае мы можем считать, что "обезьяний мир" всегда находится в некотором состоянии, и оно может изменяться со временем. Текущее состояние определяется взаиморасположением объектов. Например, исходное состояние мира определяется так:
(1) Обезьяна у двери.
(2) Обезьяна на полу.
(3) Ящик у окна.
(4) Обезьяна не имеет банана.
Удобно объединить все эти четыре информационных фрагмента в один структурный объект. Давайте в качестве такого объединяющего функтора выберем слово "состояние". На рис. 2.12 в виде структурного объекта изображено исходное состояние.
Нашу задачу можно рассматривать как игру для одного игрока. Давайте, формализуем правила этой игры.
Первое, целью игры является ситуация, в которой обезьяна имеет банан, т. е. любое состояние, у которого в качестве четвертой компоненты стоит "имеет":
состояние( -, -, -, имеет)
Второе, каковы разрешенные ходы, переводящие мир из одного состояния в другое? Существуют четыре типа ходов:
(1) схватить банан,
(2) залезть на ящик,
(3) подвинуть ящик,
(4) перейти в другое место.

Рис. 2. 12. Исходное состояние обезьяньего мира, представленное в виде структурного объекта. Его четыре компоненты суть горизонтальная позиция обезьяны, вертикальная позиция обезьяны, позиция ящика, наличие или отсутствие у обезьяны банана.
Не всякий ход допустим при всех возможных состояниях мира. Например, ход "схватить" допустим, только если обезьяна стоит на ящике прямо под бананом (т.е. в середине комнаты) и еще не имеет банана. Эти правила можно формализовать в Прологе в виде трехместного отношения ход:
ход( Состояние1, М, Состояние2)
Три аргумента этого отношения определяют ход, следующим образом:
Состояние1 --------> Состояние2
М
Состояние1 это состояние до хода, М - выполняемый ход, и Состояние2 - состояние после хода.
Ход "схватить", вместе с необходимыми ограничениями на состояние перед этим ходом, можно выразить такой формулой:
ход( состояние( середина, наящике, середина, неимеет),
% Перед ходом
схватить, % Ход
состояние( середина, наящике, середина, имеет) ).
% После хода
В этом факте говорится о том, что после хода у обезьяны уже есть банан и что она осталась на ящике в середине комнаты.
Таким же способом можно выразить и тот факт, что обезьяна, находясь на полу, может перейти из любой горизонтальной позиции Р1 в любую позицию Р2. Обезьяна может это сделать независимо от позиции ящика, а также независимо от того, есть у нее банан или нет. Все это можно записать в виде следующего прологовского факта:
ход( состояние( Р1, наполу, В, Н),
перейти( Р1, Р2), % Перейти из Р1 в Р2
состояние( Р2, наполу, В, Н) ).
Заметим, что в этом предложении делается много утверждений и, в частности: выполненный ход состоял в том, чтобы "перейти из некоторой позиции Р1 в некоторую позицию Р2"; обезьяна находится на полу, как до, так и после хода; ящик находится в некоторой точке В, которая осталась неизменной после хода; состояние "имеет банан" остается неизменным после хода.
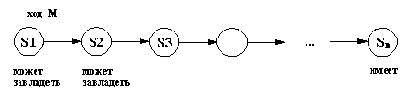
Рис. 2. 13. Рекурсивная формулировка отношения можетзавладетъ.
Данное предложение на самом деле определяет все множество возможных ходов указанного типа, так как оно применимо к любой ситуации, сопоставимой с состоянием, имеющим место перед входом.
Поэтому такое предложение иногда называют схемой хода. Благодаря понятию переменной, имеющемуся в Прологе, такие схемы легко на нем запрограммировать.
Два других типа ходов: "подвинуть" и "залезть" - легко определить аналогичным способом.
Главный вопрос, на который должна ответить наша программа, это вопрос: "Может ли обезьяна, находясь в некотором начальном состоянии S, завладеть бананом?" Его можно сформулировать в виде предиката
можетзавладеть( S)
где аргумент S - состояние обезьяньего мира. Программа для можетзавладеть может основываться на двух наблюдениях:
(1) Для любого состояния S, в которой обезьяна уже имеет банан, предикат можетзавладеть должен, конечно, быть истинным; в этом случае никаких ходов не требуется. Вот соответствующий прологовский факт:
можетзавладеть( состояние( -, -, -, имеет) ).
(2) В остальных случаях требуется один или более ходов. Обезьяна может завладеть бананом в любом состоянии S1, если для него существует ход из состояния Р1 в некоторое состояние S2, такое, что, попав в него, обезьяна уже сможет завладеть бананом (за нуль или более ходов). Этот принцип показан на рис. 2.13. Прологовская формула, соответствующая этому правилу, такова:
можетзавладеть( S1) :-
ход( S1, М, S2),
можетзавладеть( S2).
Теперь мы полностью завершили нашу программу, показанную на рис. 2.14.
Формулировка можетзавладеть рекурсивна и совершенно аналогична формулировке отношения предок из гл. 1 (ср. рис. 2.13 и 1.7). Этот принцип используется в Прологе повсеместно.
Мы создали нашу программу "непроцедурным" способом. Давайте теперь изучим ее процедурное поведение, рассмотрев следующий вопрос к программе:
?- можетзавладеть( состояние( удвери, наполу, уокна, неимеет) ).
Ответом пролог-системы будет "да". Процесс, выполняемый ею при этом, обрабатывает, в соответствии с процедурной семантикой Пролога, последовательность списков целей. Для этого требуется некоторый перебор ходов, для отыскания верного из нескольких альтернативных. В некоторых точках при таком переборе будет сделан неверный ход, ведущий в тупиковую ветвь процесса вычислений. На этом этапе автоматический возврат позволит исправить положение. На рис. 2.15 изображен процесс перебора.
line(); % Разрешенные ходы
ход( состояние( середина, на ящике, середина, неимеет),
схватить, % Схватить банан
состояние( середина, наящике, середина, имеет)).
ход( состояние( Р, наполу, Р, Н),
залезть, % Залезть на ящик
состояние( Р, наящике, Р, Н) ).
ход( состояние( Р1, наполу, Р1, Н),
подвинуть( Р1, Р2), % Подвинуть ящик с Р1 на Р2
состояние( Р2, наполу, Р2, Н) ).
ход( состояние( Р1, наполу, В, Н),
перейти( Р1, Р2), % Перейти с Р1 на Р2
состояние( Р2, наполу, В, Н) ).
% можетзавладеть(Состояние): обезьяна может завладеть
% бананом, находясь в состоянии Состояние
можетзавладеть( состояние( -, -, -, имеет) ).
% может 1: обезьяна уже его имеет
можетзавладеть( Состояние1) :-
% может 2: Сделать что-нибудь, чтобы завладеть им
ход( Состояние1, Ход, Состояние2),
% сделать что-нибудь
можетзавладеть( Состояние2).
% теперь может завладеть
line(); Рис. 2. 14. Программа для задачи об обезьяне и банане.
Для ответа на наш вопрос системе пришлось сделать лишь один возврат. Верная последовательность ходов была найдена почти сразу. Причина такой эффективности программы кроется в том порядке, в

Рис. 2. 15. Поиск банана обезьяной. Перебор начинается в верхнем узле и распространяется вниз, как показано. Альтернативные ходы перебираются слева направо. Возврат произошел только один раз.
котором в ней расположены предложения, касающиеся отношения ход. В нашем случае этот порядок (к счастью) оказался весьма подходящим. Однако возможен и менее удачный порядок. По правилам игры обезьяна могла бы с легкостью ходить туда-сюда, даже не касаясь ящика, или бесцельно двигать ящик в разные стороны. Как будет видно из следующего раздела, более тщательное исследование обнаруживает, что порядок предложений в нашей программе является, на самом деле, критическим моментом для успешного решения задачи.
Назад | Содержание | Вперёд
Пример отношений, определяющих конкретную задачу: поиск маршрута
Давайте теперь сформулируем задачу нахождения маршрута как задачу поиска в И / ИЛИ-графе, причем сделаем это таким образом, чтобы наша формулировка могла бы быть непосредственно использована процедурой и_или рис. 13.12. Мы условимся, что карта дорог будет представлена при помощи отношения
связь( Гор1, Гор2, Р)
означающего, что между городами Гор1 и Гор2 существует непосредственная связь, а соответствующее расстояние равно Р. Далее, мы допустим, что существует отношение
клпункт( Гор1-Гор2, Гор3)
имеющее следующий смысл: для того, чтобы найти маршрут из Гор1 в Гор2, следует рассмотреть пути, проходящие через Гор3 ( Гор3 - это "ключевой пункт" между Гор1 и Гор2). Например, на карте рис. 13.1 f и g - это ключевые пункты между а и z:
клпункт( a-z, f). клпункт( a-z, g).
Мы реализуем следующий принцип построения маршрута:
Для того, чтобы найти маршрут между городами X и Z, необходимо:
(1) если между X и Z имеются ключевые пункты Y1, Y2, ..., то найти один из путей:
путь из X в Z через Y1, или
путь из X в Z через Y2, или
...
(2) если между X и Z нет ключевых пунктов, то найти такой соседний с X город Y, что существует маршрут из Y в Z.
Таким образом, мы имеем два вида задач, которые мы будем представлять как
(1) X-Z найти маршрут из X в Z
(2) X-Z через Y найти маршрут из X в Z, проходящий через Y
Здесь 'через' - это инфиксный оператор более высокого приоритета, чем '-', и более низкого, чем '--->'. Теперь можно определить соответствующий И / ИЛИ-граф явным образом при помощи следующего фрагмента программы:
:- ор( 560, xfx, через)
% Правила задачи X-Z, когда между X и Z
% имеются ключевые пункты,
% стоимости всех дуг равны 0
X-Z ---> или : СписокЗадач
:- bagof( ( X-Z через Y)/0, клпункт( X-Z, Y),
СписокЗадач), !.
% Правила для задачи X-Z без ключевых пунктов
X-Z ---> или : СписокЗадач
:- bagof( ( Y-Z)/P, связь( X, Y, Р), СписокЗадач).
% Сведение задачи типа ''через" к подзадачам,
% связанным отношением И
X-Z через Y---> и : [( X-Y)/0, ( Y-Z)/0].
цель( Х-Х) % Тривиальная задача: попасть из X в X
Функцию h можно определить, например, как расстояние, которое нужно преодолеть при воздушном сообщении между городами.
программы: родственные отношения
Пролог - это язык программирования, предназначенный для обработки символьной нечисловой информации. Особенно хорошо он приспособлен для решения задач, в которых фигурируют объекты и отношения между ними. На рис. 1.1 представлен пример - родственные отношения. Тот факт, что Том является родителем Боба, можно записать на Прологе так:
родитель( том, боб).
Здесь мы выбрали родитель в качестве имени отношения, том и боб - в качестве аргументов этого отношения. По причинам, которые станут понятны позднее, мы записываем такие имена, как том, начиная со строчной буквы. Все дерево родственных отношений рис. 1.1 описывается следующей пролог-программой:
родитель( пам, боб).
родитель( том, боб).
родитель( том, лиз).
родитель( боб, энн).
родитель( боб, пат).
родитель( пам, джим).

Рис. 1. 1. Дерево родственных отношений.
Эта программа содержит шесть предложений. Каждое предложение объявляет об одном факте наличия отношения родитель.
После ввода такой программы в пролог-систему последней можно будет задавать вопросы, касающиеся отношения родитель. Например, является ли Боб родителем Пат? Этот вопрос можно передать пролог-системе, набрав на клавиатуре терминала:
?- родитель( боб, пат).
Найдя этот факт в программе, система ответит
yes (да)
Другим вопросом мог бы быть такой:
?- родитель( лиз, пат).
Система ответит
no (нет),
поскольку в программе ничего не говорится о том, является ли Лиз родителем Пат.
Программа ответит "нет" и на вопрос
?- родитель( том, бен).
потому, что имя Бен в программе даже не упоминается.
Можно задавать и более интересные вопросы. Например:"Кто является родителем Лиз?"
?- родитель( X, лиз).
На этот раз система ответит не просто "да" или "нет". Она скажет нам, каким должно быть значение X (ранее неизвестное), чтобы вышеприведенное утверждение было истинным. Поэтому мы получим ответ:
X = том
Вопрос "Кто дети Боба?" можно передать пролог-системе в такой форме:
?- родитель( боб, X).
В этом случае возможно несколько ответов. Сначала система сообщит первое решение:
X = энн
Возможно, мы захотим увидеть и другие решения. О нашем желании мы можем сообщить системе (во многих реализациях для этого надо набрать точку с запятой), и она найдет другой ответ:
X = пат
Если мы потребуем дальнейших решений, система ответит "нет", поскольку все решения исчерпаны.
Нашей программе можно задавать и более общие вопросы: "Кто чей родитель?" Приведем другую формулировку этого вопроса:
Найти X и Y такие, что X - родитель Y.
На Прологе это записывается так:
?- родитель( X, Y).
Система будет по очереди находить все пары вида "родитель-ребенок". По мере того, как мы будем требовать от системы новых решений, они будут выводиться на экран одно за другим до тех пор, пока все они не будут найдены. Ответы выводятся следующим образом:
X = пам
Y = боб;
X = том
Y = боб;
X = том
Y = лиз;
. . .
Мы можем остановить поток решений, набрав, например, точку вместо точки с запятой (выбор конкретного символа зависит от реализации).
Нашей программе можно задавать и еще более сложные вопросы, скажем, кто является родителем родителя Джима? Поскольку в нашей программе прямо не сказано, что представляет собой отношение родительродителя, такой вопрос следует задавать в два этапа, как это показано на рис. 1.2.
(1) Кто родитель Джима? Предположим, что это некоторый Y.
(2) Кто родитель Y? Предположим, что это некоторый X.
Такой составной вопрос на Прологе записывается в виде последовательности двух простых вопросов:
?- родитель( Y, джим), родитель( X, Y).
Ответ будет:
X = боб
Y = пат

Рис. 1. 2. Отношение родительродителя, выраженное через композицию двух отношений родитель.
Наш составной вопрос можно интерпретировать и так: "Найти X и Y, удовлетворяющие следующим двум требованиям":
родитель ( Y, джим) и родитель( X, У)
Если мы поменяем порядок этих двух требований, то логический смысл останется прежним:
родитель ( X, Y) и родитель ( Y, джим)
Этот вопрос можно задать нашей пролог-системе и в такой форме:
?- родитель( X, Y), родитель( Y, джим).
При этом результат будет тем же. Таким же образом можно спросить: "Кто внуки Тома?"
?- родитель( том, X), родитель( X, Y).
Система ответит так:
X = боб
Y = энн;
X = боб
Y = пат
Следующим вопросом мог бы быть такой: "Есть ли у Энн и Пат общий родитель?" Его тоже можно выразить в два этапа:
(1) Какой X является родителем Энн?
(2) Является ли (тот же) X родителем Пат?
Соответствующий запрос к пролог-системе будет тогда выглядеть так:
?- родитель( X, энн), родитель( X, пат).
Ответ:
X = боб
Наша программа-пример помогла проиллюстрировать некоторые важные моменты: На Прологе легко определить отношение, подобное отношению родитель, указав n-ку объектов, для которых это отношение выполняется. Пользователь может легко задавать пролог-системе вопросы, касающиеся отношений, определенных в программе. Пролог-программа состоит из предложений. Каждое предложение заканчивается точкой. Аргументы отношения могут быть (среди прочего): конкретными объектами, или константами (такими, как том и энн), или абстрактными объектами, такими, как X и Y. Объекты первого типа называются атомами. Объекты второго типа - переменными. Вопросы к системе состоят из одного или более целевых утверждений (или кратко целей). Последовательность целей, такая как
родитель( X, энн), родитель( X, пат)
означает конъюнкцию этих целевых утверждений:
X - родитель Энн и
X - родитель Пат.
Пролог-система рассматривает вопросы как цели, к достижению которых нужно стремиться.
Ответ на вопрос может оказаться или положительным или отрицательным в зависимости от того, может ли быть соответствующая цель достигнута или нет. В случае положительного ответа мы говорим, что соответствующая цель достижима и успешна.В противном случае цель недостижима, имеет неуспех или терпит неудачу. Если на вопрос существует несколько ответов, пролог-система найдет столько из них, сколько пожелает пользователь.
Пример составления программы
С системами, управляемыми образцами, связан свой особый стиль программирования, требующий специфического программистского мышления. Мы говорим в этом случае о программировании в терминах образцов.
В качестве иллюстрации, рассмотрим элементарное упражнение по программированию - вычисление наибольшего общего делителя D двух целых чисел А и В. Рассмотрим классический алгоритм Евклида:
line();Для того, чтобы вычислить наибольший общий делитель D чисел А и В, необходимо:
Повторять циклически, пока А и В не совпадут:
если А > В, то заменить А на А - В, иначе заменить В на В - А.
После выхода из цикла А и В совпадают; наибольший общий делитель D равен
А (или В).
Тот же самый процесс можно описать при помощи двух модулей, управляемых образцами:
Модуль 1
Условие В базе данных существуют такие два числа X и Y, что X > Y.
Действие Заменить X на разность X - Y.
Модуль 2
Условие В базе данных имеется число X.
Действие Выдать результат X и остановиться.
Очевидно, что всегда, когда условие Модуля 1 удовлетворяется, удовлетворяется также и условие Модуля 2, и мы имеем конфликт. В нашем случае конфликт можно разрешить при помощи простого управляющего правила: всегда отдавать предпочтение Модулю 1. База данных первоначально содержит числа А и В.
Здесь нас ждет приятный сюрприз: оказывается, что наша программа способна решать более общую задачу, а именно, она может вычислять наибольший общий делитель для любого количества чисел.
Если в базу данных загрузить несколько целых чисел, то программа выведет их наибольший общий делитель. На рис. 16.3 показана возможная последовательность изменений, которые претерпевает база данных прежде, чем будет получен результат. Обратите внимание на то, что предварительные условия модулей могут удовлетворяться одновременно в нескольких местах базы данных.

Рис. 16. 3. Процесс вычисления наибольшего общего делителя
множества чисел. Первоначально база данных содержит числа
25, 10, 15 и 30. Вертикальная стрелка соединяет число с его
"заменителем". Конечное состояние базы данных: 5, 5, 5, 5.
В данной главе мы реализуем интерпретатор простого языка для описания систем, управляемых образцами, и проиллюстрируем на примерах дух программирования в терминах образцов.
Назад | Содержание | Вперёд
Принадлежность к списку
Мы представим отношение принадлежности как
принадлежит( X, L)
где Х - объект, а L - список. Цель принадлежит( X, L) истинна, если элемент Х встречается в L. Например, верно что
принадлежит( b, [а, b, с] )
и, наоборот, не верно, что
принадлежит b, [а, [b, с] ] )
но
принадлежит [b, с], [а, [b, с]] )
истинно. Составление программы для отношения принадлежности может быть основано на следующих соображениях:
(1) Х есть голова L, либо
(2) Х принадлежит хвосту L.
Это можно записать в виде двух предложений, первое из которых есть простой факт, а второе - правило:
принадлежит( X, [X | Хвост ] ).
принадлежит ( X, [Голова | Хвост ] ) :-
принадлежит( X, Хвост).
Принципы реализации
Давайте сначала расширим правила языка, с тем чтобы получить возможность работать с неопределенностью. К каждому, правилу мы можем добавить "силовой модификатор", определяемый двумя неотрицательными действительными числами S и N. Вот соответствующий формат:
Имя Правила: если
Условие
то
Заключение
с
Сила( N, S).
Примеры правил рис. 14.14 можно изобразить в этой форме так:
прав1 : если
не давлоткр и
открклап
то
открклрано
с
сила( 0.001, 2000).
прав2 : если
сепзапвд
то
давлоткр
с
сила( 0.05, 400).
Для того, чтобы произвести соответствующее расширение оболочки экспертной системы (разд. 14.5), нам понадобится внести изменения в большинство процедур. Давайте сосредоточимся только на одной из них, а именно на процедуре
рассмотреть( Цель, Трасса, Ответ)
Мы предположим, что утверждение Цель
не содержит переменных (как это сделано в Prospector'e и в AL/X). Это сильно упростит дело (особенно в процедуре ответпольз). Таким образом, Цель
будет логической комбинацией элементарных утверждений. Например:
не давлоткр и открклап
Цепочку целей-предков и правил Трасса
можно представить таким же способом, как это сделано в разд. 14.5. Однако форму представления объекта Ответ придется модифицировать для того, чтобы включить в нее вероятности. Цель и ее вероятность можно соединить в один терм следующим образом:
Цель : Вероятность
Получим такой пример объекта Ответ:
индоткр : 1 было сказано
Смысл ответа: пользователь сообщил системе, что событие индоткр произошло, и что это абсолютно достоверно.
Представление объекта Ответ требует еще одной модификации, в связи с тем, что в одно и то же событие могут вести несколько независимых связей, которые все окажут влияние на вероятность этого события - его шанс будет помножен (рис. 14.15) на все множители. В этом случае Ответ
будет содержать список всех ветвей вывода заключения. Приведем пример ответа такого рода для сети рис. 14.14 (для наглядности расположенный на нескольких строках):
давлоткр : 1 было 'выведено по'
[ прав2 из сепзапвд : 1 было сказано,
прав5 из диагсеп : 1 было сказано ]
Процедура рассмотреть, выдающая ответы в такой форме, показана на рис. 14.16.
Она обращается к предикату
импликация( Р0, Р, Сила, Вер0, Вер)
соответствующему отношению "мягкой импликации" (см. рис. 14.15). Р0 - априорная вероятность события Е, а Р - его апостериорная вероятность. Сила
- сила импликации, представленная как
сила( N, S)
Вер0 и Вер - соответственно априорная и апостериорная вероятности гипотезы H.
Следует заметить, что наша реализация очень проста, она обеспечивает только изменение вероятностей при распространении информации по сети вывода и иногда ведет себя недостаточно разумно. Никакого внимания не уделяется отбору для анализа наиболее важной в данный момент информации. В более сложной версии следовало бы направлять процесс поиска ответа в сторону наиболее существенных фактов. Кроме того, необходимо стремиться к тому, чтобы пользователю задавалось как можно меньше вопросов.
Наконец, несколько замечаний относительно новой версии процедуры ответпольз. Она будет проще, чем процедура рис. 14.11, так как в запросах, передаваемых пользователю, уже не будет переменных. На этот раз пользователь в качестве ответа введет некоторую вероятность (вместо "да" или "нет"). Если пользователю ничего неизвестно о событии, содержащемся в вопросе, то вероятность этого события не изменится. Пользователь может также задать вопрос "почему" и получить изображение объекта Трасса в качестве объяснения. Кроме того, следует разрешить пользователю задавать вопрос: "Какова текущая вероятность моей гипотезы?" Тогда, если он устал вводить новую информацию (или у него мало времени), он может прекратить консультационный сеанс, довольствуясь ответом системы, полученным на основании неполной информации.
line();
% Процедура
% рассмотреть( Цель, Трасса, Ответ)
%
% находит степень правдоподобия утверждения "цель это правда".
% Оценка правдоподобия содержится в объекте Ответ.
Трасса - это
% цепочка целей-предшественников и правил, которую можно
% использовать в объяснении типа "почему"
рассмотреть( Цель, Трасса, ( Цель: Вер) было
'выведено по' ПравОтв) :-
bagof( Прав: если Условие то Цель с Сила, Правила),
% Все правила, относящиеся к цели
априори( Цель, Вер0),
% Априорная вероятность цели
модиф( Вер0, Правила, Трасса, Вер, ПравОтв).
% Модифицировать априорные вероятности
рассмотреть( Цель1 и Цель2, Трасса,
( Цель1 и Цель2 : Вер было 'выведено из'
( Ответ1 и Ответ2) ) :-
!,
рассмотреть( Цель1, Трасса, Ответ1),
рассмотреть( Цель2, Трасса, Ответ2),
вероятность( Ответ1, В1),
вероятность( Ответ2, В2),
мин( В1, В2, Вер).
рассмотреть( Цель1 или Цель2, Трасса,
( Цель или Цель2:Вер) было 'выведено из'
( Ответ1 и Ответ2) ) :-
!,
рассмотреть( Цель1, Трасса, Ответ1),
рассмотреть( Цель2, Трасса, Ответ2),
вероятность( Ответ1, В1),
вероятность( Ответ2, В2),
макс( В1, В2, Вер).
рассмотреть( не Цель, Трасса,
( не Цель:Вер) было 'выведено из' Ответ) :-
!,
рассмотреть( Цель, Трасса, Ответ),
вероятность( Ответ, В),
обратить( В, Вер).
рассмотреть( Цель, Трасса, ( Цель: Вер) было сказано) :-
ответпольз( Цель, Трасса, Вер).
% Ответ, выведенный пользователем
% Отношение
%
% модиф( Вер0, Правила, Трасса, Вер, ПравОтв)
%
% Существует Цель с априорной вероятностью Вер0. Правила имеют
% отношение к утверждению Цель; суммарное влияние этих правил
% (точнее, их условных частей) на Вер0 приводит к тому,
% что Вер0 заменяется на апостериорную вероятность Вер;
% Трасса - список целей-предков и правил, использовавшихся
% при выводе утверждения Цель;
% ПравОтв - результаты анализа условных частей
% правил из списка Правила.
модиф( Вер0, [ ], Трасса, Вер0, [ ]).
% Нет правил - нет модификации
модиф( Вер0,
[ Прав : если Усл то Цель с Сила | Правила],
Трасса, Вер, [Прав из Ответ | ПравОтв] ):-
рассмотреть( Усл, [Цель по Прав | Трасса], Ответ),
% Условие из первого правила
априори( Усл, В0),
вероятность( Ответ, В),
импликация( В0, В, Сила, Вер0, Вер1),
% "Мягкая" импликация
модиф( Вер1, Правила, Трасса, Вер, ПравОтв).
line();
Рис. 14. 16. Определение степени правдоподобия гипотезы при помощи
распространения информации об оценке уверенности по сети вывода.
Назад | Содержание
| Вперёд
Процедура ответпольз
Прежде чем перейти к написанию процедуры ответпольз, давайте рассмотрим одну полезную вспомогательную процедуру
принять( Ответ)
В процессе диалога часто возникает ситуация, когда от пользователя ожидается ответ "да", "нет" или "почему". Процедура принять предназначена для того, чтобы извлечь один из этих ответов, понимая его правильно и в тех случаях, когда пользователь применяет сокращения ('д' или 'н') или делает ошибки. Если ответ пользователя непонятен, то принять просит дать другой вариант ответа.
принять( Ответ) :-
read( Ответ1),
означает( Ответ1, Значение), !,
% Ответ1 означает что-нибудь?
Ответ = Значение; % Да
nl, write( 'Непонятно, попробуйте еще раз, % Нет
пожалуйста'), nl,
принять( Ответ). % Новая попытка
означает( да, да).
означает( д, да).
означает( нет, нет).
означает( н, нет).
означает( почему, почему).
означает( п, почему).
Следует заметить, что процедурой принять нужно пользоваться с осторожностью, так как она содержит взаимодействие с пользователем. Следующий фрагмент программы может служить примером неудачной попытки запрограммировать интерпретацию ответов пользователя:
принять( да), интерп_да( ...);
принять( нет), интерп_нет( ...);
. . .
Здесь, если пользователь ответит "нет", то программа попросит его повторить свой ответ. Поэтому более правильный способ такой:
принять( Ответ),
( Ответ = да, интерп_да( ...);
Ответ = нет, интерп_нет( ...);
... )
Процедура
ответпольз( Цель, Трасса, Ответ)
спрашивает пользователя об истинности утверждения Цель. Ответ - это результат запроса. Трасса используется для объяснения в случае, если пользователь спросит "почему".
Сначала процедура ответпольз должна проверить, является ли Цель информацией, которую можно запрашивать у пользователя. Это свойство объекта Цель задается отношением
можно_спросить( Цель)
которое в дальнейшем будет усовершенствовано. Если спросить можно, то утверждение Цель выдается пользователю, который, в свою очередь, указывает истинно оно или ложно. Если пользователь спросит "почему", то ему выдается Трасса.
Если утверждение Цель истинно, то пользователь укажет также значения содержащихся в нем переменных (если таковые имеются).
Все вышеизложенное можно запрограммировать (в качестве первой попытки) следующим образом:
остветпольз( Цель, Трасса, Ответ) :-
можно_спросить( Цель), % Можно ли спрашивать
спросить( Цель, Трасса, Ответ).
% Задать вопрос относительно утверждения Цель
спросить( Цель, Трасса, Ответ) :-
показать( Цель),
% Показать пользователю вопрос
принять(Ответ1), % Прочесть ответ
обработать( Ответ1, Цель, Трасса, Ответ).
% Обработать ответ
обработать( почему, Цель, Трасса, Ответ) :-
% Задан вопрос "почему"
показать_трассу( Трасса),
% Выдача ответа на вопрос "почему"
спросить( Цель, Трасса, Ответ).
% Еще раз спросить
обработать( да, Цель, Трасса, Ответ) :-
% Пользователь ответил, что Цель истинна
Ответ = правда,
запрос_перем( Цель);
% Вопрос о значении переменных
спросить( Цель, Трасса, Ответ).
% Потребовать от пользователя новых решений
обработать( нет, Цель, Трасса, ложь).
% Пользователь ответил, что Цель ложна
показать( Цель) :-
nl, write( 'Это правда:'),
write( Цель), write( ?), nl.
Обращение к процедуре запрос_перем( Цель) нужно для того, чтобы попросить пользователя указать значение каждой из переменных, содержащихся в утверждении Цель:
запрос_перем( Терм) :-
var( Терм), !, % Переменная ?
nl, write( Терм), write( '='),
read( Терм). % Считать значение переменной
запрос_перем( Терм) :-
Терм =.. [Функтор | Аргументы],
% Получить аргументы структуры
запрос_арг( Аргументы).
% Запросить значения переменных в аргументах
запрос_арг( [ ]).
запрос_арг( [Терм | Термы]) :-
запрос_перем( Терм),
запрос_арг( Термы).
Проведем несколько экспериментов с процедурой ответпольз. Пусть, например, известно, что пользователя можно спрашивать о наличии бинарного отношения ест:
можно_спросить( X ест Y).
( В приведенных ниже диалогах между пролог-системой и пользователем тексты пользователя даются полужирным шрифтом, а реплики пролог-системы курсивом).
?- ответпольз( питер ест мясо, [ ], Ответ).
Это правда: питер ест мясо? % Вопрос пользователю
да. % Ответ пользователя
Ответ = правда
Более интересный пример диалога (с использованием переменных) мог бы выглядеть примерно так:
?- ответпольз( Кто ест Что, [ ], Ответ).
Это правда: _17 ест _18?
% Пролог дает переменным свои внутренние имена
да.
_17 = питер.
_18 = мясо.
Ответ = правда.
Кто = питер
Что = мясо; % Возврат для получения других решений
Это правда: _17 ест _18?
да.
_17 = сьюзен.
_18 = бананы.
Ответ = правда
Кто = сьюзен
Что = бананы;
Это правда : _17 ест _18?
нет.
Ответ = ложь
Процедура проверки принадлежности списку, дающая единственное решение
Для того, чтобы узнать, принадлежит ли Х списку L, мы пользовались отношением
принадлежит( X, L)
Программа была следующей:
принадлежит( X, [X | L] ).
принадлежит X, [Y | L] ) :- принадлежит( X, L).
Эта программа дает "недетерминированный" ответ: если Х встречается в списке несколько раз, то будет найдено каждое его вхождение. Исправить этот недостаток не трудно: нужно только предотвратить дальнейший перебор сразу же после того, как будет найден первый X, а это произойдет, как только в первом предложении наступит успех. Измененная программа выглядит так:
принадлежит( X, [X | L] ) :- !.
принадлежит( X, [Y | L] ) :- принадлежит( X, L).
Эта программа породит только одно решение. Например:
?- принадлежит( X, [а, b, с] ).
Х = а;
nо
(нет)
Процедура рассмотреть
Центральной процедурой оболочки является процедура
рассмотреть( Цель, Трасса, Ответ)
которая будет находить ответ Ответ на заданный вопрос Цель, используя принципы, намеченные в общих чертах в разд. 14.4.1: найти Цель среди фактов базы знаний, или применить правило из базы знаний, или спросить пользователя, или же обработать Цель как И / ИЛИ-комбинацию подцелей.
Аргументы имеют следующий смысл и следующую структуру:
Цель
вопрос, подлежащий рассмотрению, представленный
как И / ИЛИ-комбинация простых утверждений, например
X имеет перья или X летает или
X откладывает яйца
Трасса цепочка, составленная из целей-предков и правил,
расположенных между Цель и исходной целью самого верхнего уровня. Представляется как список, состоящий из элементов вида
Цель по Прав
что означает: Цель рассматривалась с использованием правила Прав. Например, пусть исходной целью будет "питер это тигр", а текущей целью - "питер ест мясо". В соответствии с базой знаний рис. 14.5 имеем трассу
[( питер это хищник) по прав3,
( питер это тигр) по прав5 ]
Смысл ее можно выразить так:
Я могу использовать " питер ест мясо" для того, чтобы проверить по прав3, что "питер это хищник".
Далее, я могу использовать "питер это хищник" для того, чтобы проверить по прав5, что "питер это тигр".
Ответ решающее И / ИЛИ-дерево для вопроса Цель. Общая форма
представления для объекта Ответ:
Заключение было Найдено
где Найдено - это обоснование для результата Заключение. Следующие три примера иллюстрируют различные варианты ответов:
(1) ( соед( радиатор, предохр1) это правда) было
'найдено как факт'
(2) (питер ест мясо) это ложь было сказано
(3) (питер это хищник) это правда было
( 'выведено по' прав3 из
(питер это млекопитающее) это правда было
( 'выведено по' прав1 из
(питер имеет шерсть) это правда было сказано)
и
(питер ест мясо) это правда было сказано )
На рис. 14. 10 показана прологовская программа для процедуры рассмотреть. В этой программе реализованы принципы разд. 14.4.1 с использованием только что описанных структур данных.
line(); % Процедура
%
% рассмотреть( Цель, Трасса, Ответ)
%
% находит Ответ на вопрос Цель. Трасса - это цепочка
% целей-предков и правил. "рассмотреть" стремится найти
% положительный ответ на вопрос. Ответ "ложь" выдается
% только в том случае, когда рассмотрены все возможности,
% и все они дали результат "ложь".
:-ор( 900, xfx, :).
:-ор( 800, xfx, было).
:-ор( 870, fx, если).
:-ор( 880, xfx, то).
:-ор( 550, xfy, или).
:-ор( 540, xfy, и).
:- ор( 300, fx, 'выведено по').
:- ор( 600, xfx, из).
:- ор( 600, xfx, по).
% В программе предполагается,что ор( 700, хfх, это), ор( 500, fx, не)
рассмотреть( Цель, Трасса, Цель это правда
было 'найдено как факт') :-
факт : Цель.
% Предполагается, что для каждого типа цели
% существует только одно правило
рассмотреть( Цель, Трасса,
Цель это ПравдаЛожь
было 'выведено по' Прав из Ответ) :-
Прав : если Условие то Цель,
% Правило, относящееся к цели
рассмотреть( Условие, [Цель по Прав | Трасса], Ответ),
истинность( Ответ, ПравдаЛожь).
рассмотреть( Цель1 и Цель2, Трасса, Ответ) :- !,
рассмотреть( Цель1, Трасса, Ответ1),
продолжить( Ответ1, Цель1 и Цель2, Трасса, Ответ).
рассмотреть( Цель1 или Цель2, Трасса, Ответ) :-
рассм_да( Цель1, Трасса, Ответ);
% Положительный ответ на Цель1
рассм_да( Цель2, Трасса, Ответ).
% Положительный ответ на Цель2
рассмотреть( Цель1 или Цель2, Трасса,
Ответ1 и Ответ2) :- !,
not рассм_да( Цель1, Трасса, _ ),
not рассм_да( Цель2, Трасса, _ ),
% Нет положительного ответа
рассмотреть( Цель1, Трасса, Ответ1),
% Ответ1 отрицательный
рассмотреть( Цель2, Трасса, Ответ2).
% Ответ2 отрицательный
рассмотреть( Цель, Трасса,
Цель это Ответ было сказано) :-
ответпольз( Цель, Трасса, Ответ). % Ответ дан пользователем
рассм_да( Цель, Трасса, Ответ) :-
рассмотреть( Цель, Трасса, Ответ),
положительный( Ответ).
продолжить( Ответ1, Цель1 и Цель2, Трасса, Ответ) :-
положительный( Ответ1),
рассмотреть( Цель2, Трасса, Ответ2),
( положительный( Ответ2), Ответ = Ответ1 и Ответ2;
отрицательный( Ответ2), Ответ = Ответ2).
продолжить( Ответ1, Цель1 и Цель2, _, Ответ1) :-
отрицательный( Ответ1).
истинность( Вопрос это ПравдаЛожь было Найдено,
ПравдаЛожь) :- !.
истинность( Ответ1 и Ответ2, ПравдаЛожь) :-
истинность( Ответ1, правда),
истинность( Ответ2, правда), !,
ПравдаЛожь = правда;
ПравдаЛожь = ложь.
положительный( Ответ) :-
истинность( Ответ, правда).
отрицательный( Ответ) :-
истинность( Ответ, ложь).
line(); Рис. 14. 10. Основная процедура оболочки экспертной системы.
Процедура выдать
Процедура
выдать( Ответ)
приведенная на рис. 14.12, показывает пользователю окончательный результат консультационного сеанса и дает объяснения типа "как". Ответ включает в себя как ответ на вопрос пользователя, так и дерево вывода, демонстрирующее как система пришла к такому заключению. Сначала процедура выдать представляет пользователю свое заключение. Затем, если пользователь пожелает узнать, как это заключение достигнуто, то печатается дерево вывода в некоторой удобной для восприятия форме - это и есть объяснение типа "как". Форма объяснения показана в примере разд. 14.4.3.
Процедурная семантика
Процедурная семантика определяет, как пролог-система отвечает на вопросы. Ответить на вопрос - это значит удовлетворить список целей. Этого можно добиться, приписав встречающимся переменным значения таким образом, чтобы цели логически следовали из программы. Можно сказать, что процедурная семантика Пролога - это процедура вычисления списка целей с учетом заданной программы. "Вычислить цели" это значит попытаться достичь их.
Назовем эту процедуру вычислить. Как показано на рис. 2.9, входом и выходом этой процедуры являются:
входом - программа и список целей,
выходом - признак успех/неуспех и подстановка переменных.

Рис. 2. 9. Входы и выходы процедуры вычисления списка целей.
Смысл двух составляющих выхода такой:
(1) Признак успех/неуспех принимает значение "да", если цели достижимы, и "нет" - в противном случае. Будем говорить, что "да" сигнализирует об успешном завершении и "нет" - о неуспехе.
(2) Подстановка переменных порождается только в случае успешного завершения; в случае неуспеха подстановка отсутствует.
line();ПРОГРАММА
большой( медведь).
% Предложение 1
большой( слон).
% Предложение 2
маленький( кот).
% Предложение 3
коричневый ( медведь).
% Предложение 4
черный ( кот).
% Предложение 5
серый( слон).
% Предложение 6
РЕЛМШИ( Z) :- % оПЕДКНФЕМХЕ 7:
ВЕПМШИ( Z). % КЧАНИ ВЕПМШИ
% НАЗЕЙР ЪБКЪЕРЯЪ РЕЛМШЛ
РЕЛМШИ( Z) :- % оПЕДКНФЕМХЕ 8:
ЙНПХВМЕБШИ( Z). % кЧАНИ ЙНПХВМЕБШИ
% НАЗЕЙР ЪБКЪЕРЯЪ РЕЛМШЛ
бнопня
?- РЕЛМШИ( X), АНКЭЬНИ( X) % йРН НДМНБПЕЛЕММН РЕЛМШИ
% Х АНКЭЬНИ?
ьюцх бшвхякемхъ
(1) хЯУНДМШИ ЯОХЯНЙ ЖЕКЕБШУ СРБЕПФДЕМХИ:
РЕЛМШИ( X), АНКЭЬНИ( X).
(2) оПНЯЛНРП БЯЕИ ОПНЦПЮЛЛШ НР МЮВЮКЮ Й ЙНМЖС Х ОНХЯЙ ОПЕДКНФЕМХЪ, С ЙНРНПНЦН ЦНКНБЮ ЯНОНЯРЮБХЛЮ Я ОЕПБШЛ ЖЕКЕБШЛ СРБЕПФДЕМХЕЛ
РЕЛМШИ( X).
мЮИДЕМЮ ТНПЛСКЮ 7:
РЕЛМШИ( Z) :- ВЕПМШИ( Z).
гЮЛЕМЮ ОЕПБНЦН ЖЕКЕБНЦН СРБЕПФДЕМХЪ ЙНМЙПЕРХГХПНБЮММШЛ РЕКНЛ ОПЕДКНФЕМХЪ 7 - ОНПНФДЕМХЕ МНБНЦН ЯОХЯЙЮ ЖЕКЕБШУ СРБЕПФДЕМХИ.
ВЕПМШИ( X), АНКЭЬНИ( X)
(3) оПНЯЛНРП ОПНЦПЮЛЛШ ДКЪ МЮУНФДЕМХЪ ОПЕДКНФЕМХЪ, ЯНОНЯРЮБХЛНЦН Я ВЕПМШИ( X). мЮИДЕМН ОПЕДКНФЕМХЕ 5: ВЕПМШИ ( ЙНР). с ЩРНЦН ОПЕДКНФЕМХЪ МЕР РЕКЮ, ОНЩРНЛС ЯОХЯНЙ ЖЕКЕИ ОПХ ЯННРБЕРЯРБСЧЫЕИ ЙНМЙПЕРХГЮЖХХ ЯНЙПЮЫЮЕРЯЪ ДН
АНКЭЬНИ( ЙНР)
(4) оПНЯЛНРП ОПНЦПЮЛЛШ Б ОНХЯЙЮУ ЖЕКХ АНКЭЬНИ( ЙНР). мХ НДМН ОПЕДКНФЕМХЕ МЕ МЮИДЕМН. оНЩРНЛС ОПНХЯУНДХР БНГБПЮР Й ЬЮЦС (3) Х НРЛЕМЮ ЙНМЙПЕРХГЮЖХХ у = ЙНР. яОХЯНЙ ЖЕКЕИ РЕОЕПЭ ЯМНБЮ
ВЕПМШИ( X), АНКЭЬНИ( X)
оПНДНКФЕМХЕ ОПНЯЛНРПЮ ОПНЦПЮЛЛШ МХФЕ ОПЕДКНФЕМХЪ 5. мХ НДМН ОПЕДКНФЕМХЕ МЕ МЮИДЕМН. оНЩРНЛС БНГБПЮР Й ЬЮЦС (2) Х ОПНДНКФЕМХЕ ОПНЯЛНРПЮ МХФЕ ОПЕДКНФЕМХЪ 7. мЮИДЕМН ОПЕДКНФЕМХЕ (8):
РЕЛМШИ( Z) :- ЙНПХВМЕБШИ( Z).
гЮЛЕМЮ ОЕПБНИ ЖЕКХ Б ЯОХЯЙЕ МЮ ЙНПХВМЕБШИ( у), ВРН ДЮЕР
ЙНПХВМЕБШИ( X), АНКЭЬНИ( X)
(5) оПНЯЛНРП ОПНЦПЮЛЛШ ДКЪ НАМЮПСФЕМХЪ ОПЕДКНФЕМХЪ, ЯНОНЯРЮБХЛНЦН ЙНПХВМЕБШИ( X). мЮИДЕМН ОПЕДКНФЕМХЕ ЙНПХВМЕБШИ( ЛЕДБЕДЭ). с ЩРНЦН ОПЕДКНФЕМХЪ МЕР РЕКЮ, ОНЩРНЛС ЯОХЯНЙ ЖЕКЕИ СЛЕМЭЬЮЕРЯЪ ДН
АНКЭЬНИ( ЛЕДБЕДЭ)
(6) оПНЯЛНРП ОПНЦПЮЛЛШ Х НАМЮПСФЕМХЕ ОПЕДКНФЕМХЪ АНКЭЬНИ( ЛЕДБЕДЭ). с МЕЦН МЕР РЕКЮ, ОНЩРНЛС ЯОХЯНЙ ЖЕКЕИ ЯРЮМНБХРЯЪ ОСЯРШЛ. щРН СЙЮГШБЮЕР МЮ СЯОЕЬМНЕ ГЮБЕПЬЕМХЕ, Ю ЯННРБЕРЯРБСЧЫЮЪ ЙНМЙПЕРХГЮЖХЪ ОЕПЕЛЕММШУ РЮЙНБЮ:
line(); пХЯ. 2. 10. оПХЛЕП, ХККЧЯРПХПСЧЫХИ ОПНЖЕДСПМСЧ ЯЕЛЮМРХЙС
оПНКНЦЮ: ЬЮЦХ БШВХЯКЕМХИ, БШОНКМЪЕЛШУ ОПНЖЕДСПНИ БШВХЯКХРЭ.
б ЦКЮБЕ 1 Б ПЮГД. "йЮЙ ОПНКНЦ- ЯХЯРЕЛЮ НРБЕВЮЕР МЮ БНОПНЯШ" ЛШ СФЕ ТЮЙРХВЕЯЙХ ПЮЯЯЛНРПЕКХ, ВРН ДЕКЮЕР ОПНЖЕДСПЮ БШВХЯКХРЭ. б НЯРЮБЬЕИЯЪ ВЮЯРХ ДЮММНЦН ПЮГДЕКЮ ОПХБНДХРЯЪ МЕЯЙНКЭЙН АНКЕЕ ТНПЛЮКЭМНЕ Х ЯХЯРЕЛЮРХВЕЯЙНЕ НОХЯЮМХЕ ЩРНЦН ОПНЖЕЯЯЮ, ЙНРНПНЕ ЛНФМН ОПНОСЯРХРЭ АЕГ ЯЕПЭЕГМНЦН СЫЕПАЮ ДКЪ ОНМХЛЮМХЪ НЯРЮКЭМНЦН ЛЮРЕПХЮКЮ ЙМХЦХ.
йНМЙПЕРМШЕ НОЕПЮЖХХ, БШОНКМЪЕЛШЕ Б ОПНЖЕЯЯЕ БШВХЯКЕМХЪ ЖЕКЕБШУ СРБЕПФДЕМХИ, ОНЙЮГЮМШ МЮ ПХЯ. 2.10. бНГЛНФМН, ЯКЕДСЕР ХГСВХРЭ ЩРНР ПХЯСМНЙ ОПЕФДЕ, ВЕЛ ГМЮЙНЛХРЭЯЪ Я ОНЯКЕДСЧЫХЛ НАЫХЛ НОХЯЮМХЕЛ.
вРНАШ БШВХЯКХРЭ ЯОХЯНЙ ЖЕКЕБШУ СРБЕПФДЕМХИ
G1, G2, ..., Gm
ОПНЖЕДСПЮ БШВХЯКХРЭ ДЕКЮЕР ЯКЕДСЧЫЕЕ:
line(); еЯКХ ЯОХЯНЙ ЖЕКЕИ ОСЯР - ГЮБЕПЬЮЕР ПЮАНРС СЯОЕЬМН. еЯКХ ЯОХЯНЙ ЖЕКЕИ МЕ ОСЯР, ОПНДНКФЮЕР ПЮАНРС, БШОНКМЪЪ (НОХЯЮММСЧ ДЮКЕЕ) НОЕПЮЖХЧ 'опнялнрп'. опнялнрп: оПНЯЛЮРПХБЮЕР ОПЕДКНФЕМХЪ ОПНЦПЮЛЛШ НР МЮВЮКЮ Й ЙНМЖС ДН НАМЮПСФЕМХЪ ОЕПБНЦН ОПЕДКНФЕМХЪ я, РЮЙНЦН, ВРН ЦНКНБЮ я ЯНОНЯРЮБХЛЮ Я ОЕПБНИ ЖЕКЭЧ G1. еЯКХ РЮЙНЦН ОПЕДКНФЕМХЪ НАМЮПСФХРЭ МЕ СДЮЕРЯЪ, РН ПЮАНРЮ ГЮЙЮМВХБЮЕРЯЪ МЕСЯОЕУНЛ.
еЯКХ я МЮИДЕМН Х ХЛЕЕР БХД
м :- B1, ..., бn.
РН ОЕПЕЛЕММШЕ Б я ОЕПЕХЛЕМНБШБЮЧРЯЪ, ВРНАШ ОНКСВХРЭ РЮЙНИ БЮПХЮМР я' ОПЕДКНФЕМХЪ я, Б ЙНРНПНЛ МЕР НАЫХУ ОЕПЕЛЕММШУ ЯН ЯОХЯЙНЛ G1, ..., Gm. оСЯРЭ я' - ЩРН
м' :- B1', ..., бn'.
яНОНЯРЮБКЪЕРЯЪ G1 Я H'; ОСЯРЭ S - ПЕГСКЭРХПСЧЫЮЪ ЙНМЙПЕРХГЮЖХЪ ОЕПЕЛЕММШУ. б ЯОХЯЙЕ ЖЕКЕИ G1, G2, .... Gm, ЖЕКЭ G1 ГЮЛЕМЪЕРЯЪ МЮ ЯОХЯНЙ б1', .., бn', ВРН ОНПНФДЮЕР МНБШИ ЯОХЯНЙ ЖЕКЕИ:
б1', ..., бn', G2, ..., Gm
(гЮЛЕРХЛ, ВРН, ЕЯКХ я - ТЮЙР, РНЦДЮ n=0, Х Б ЩРНЛ ЯКСВЮЕ МНБШИ ЯОХЯНЙ ЖЕКЕИ НЙЮГШБЮЕРЯЪ ЙНПНВЕ, МЕФЕКХ ХЯУНДМШИ; РЮЙНЕ СЛЕМЭЬЕМХЕ ЯОХЯЙЮ ЖЕКЕИ ЛНФЕР Б НОПЕДЕКЕММШУ ЯКСВЮЪУ ОПЕБПЮРХРЭ ЕЦН Б ОСЯРНИ, Ю ЯКЕДНБЮРЕКЭМН, - ОПХБЕЯРХ Й СЯОЕЬМНЛС ГЮБЕПЬЕМХЧ.)
оЕПЕЛЕММШЕ Б МНБНЛ ЯОХЯЙЕ ЖЕКЕИ ГЮЛЕМЪЧРЯЪ МНБШЛХ ГМЮВЕМХЪЛХ, ЙЮЙ ЩРН ОПЕДОХЯШБЮЕР ЙНМЙПЕРХГЮЖХЪ S, ВРН ОНПНФДЮЕР ЕЫЕ НДХМ ЯОХЯНЙ ЖЕКЕИ
б1'', .... бn", G2', ..., Gm'
бШВХЯКЪЕР (ХЯОНКЭГСЪ ПЕЙСПЯХБМН РС ФЕ ЯЮЛСЧ ОПНЖЕДСПС) ЩРНР МНБШИ ЯОХЯНЙ ЖЕКЕИ. еЯКХ ЕЦН БШВХЯКЕМХЕ ГЮБЕПЬЮЕРЯЪ СЯОЕЬМН, РН Х БШВХЯКЕМХЕ ХЯУНДМНЦН ЯОХЯЙЮ ЖЕКЕИ РНФЕ ГЮБЕПЬЮЕРЯЪ СЯОЕЬМН. еЯКХ ФЕ ЕЦН БШВХЯКЕМХЕ ОНПНФДЮЕР МЕСЯОЕУ, РНЦДЮ МНБШИ ЯОХЯНЙ ЖЕКЕИ НРАПЮЯШБЮЕРЯЪ Х ОПНХЯУНДХР БНГБПЮР Й ОПНЯЛНРПС ОПНЦПЮЛЛШ. щРНР ОПНЯЛНРП ОПНДНКФЮЕРЯЪ, МЮВХМЮЪ Я ОПЕДКНФЕМХЪ, МЕОНЯПЕДЯРБЕММН ЯКЕДСЧЫЕЦН ГЮ ОПЕДКНФЕМХЕЛ я (я - ОПЕДКНФЕМХЕ, ХЯОНКЭГНБЮБЬЕЕЯЪ ОНЯКЕДМХЛ) Х ДЕКЮЕРЯЪ ОНОШРЙЮ ДНЯРХВЭ СЯОЕЬМНЦН ГЮБЕПЬЕМХЪ Я ОНЛНЫЭЧ ДПСЦНЦН ОПЕДКНФЕМХЪ. line(); аНКЕЕ ЙНЛОЮЙРМЮЪ ГЮОХЯЭ ЩРНИ ОПНЖЕДСПШ Б НАНГМЮВЕМХЪУ, АКХГЙХУ Й оЮЯЙЮКЧ, ОПХБЕДЕМЮ МЮ ПХЯ. 2.11.
гДЕЯЭ ЯКЕДСЕР ЯДЕКЮРЭ МЕЯЙНКЭЙН ДНОНКМХРЕКЭМШУ ГЮЛЕВЮМХИ, ЙЮЯЮЧЫХУЯЪ ОПНЖЕДСПШ БШВХЯКХРЭ Б РНЛ БХДЕ, Б ЙНРНПНЛ НМЮ ОПХБНДХРЯЪ. бН-ОЕПБШУ, Б МЕИ ЪБМН МЕ СЙЮГЮМН, ЙЮЙ ОНПНФДЮЕРЯЪ НЙНМВЮРЕКЭМЮЪ ПЕГСКЭРХПСЧЫЮЪ ЙНМЙПЕРХГЮЖХЪ ОЕПЕЛЕММШУ. пЕВЭ ХДЕР Н ЙНМЙПЕРХГЮЖХХ S, ЙНРНПЮЪ ОПХБНДХР Й СЯОЕЬМНЛС ГЮБЕПЬЕМХЧ Х ЙНРНПЮЪ, БНГЛНФМН, СРНВМЪКЮЯЭ ОНЯКЕДСЧЫХЛХ ЙНМЙПЕРХГЮЖХЪЛХ БН БПЕЛЪ БКНФЕММШУ ПЕЙСПЯХБМШУ БШГНБНБ БШВХЯКХРЭ.
line(); procedure БШВХЯКХРЭ (оПНЦП, яОХЯНЙжЕКЕИ, сЯОЕУ)
бУНДМШЕ ОЮПЮЛЕРПШ:
оПНЦП: ЯОХЯНЙ ОПЕДКНФЕМХИ
яОХЯНЙжЕКЕИ: ЯОХЯНЙ ЖЕКЕИ
бШУНДМНИ ОЮПЮЛЕРП:
сЯОЕУ: ХЯРХММНЯРМНЕ ГМЮВЕМХЕ; сЯОЕУ ОПХМХЛЮЕР ГМЮВЕМХЕ
ХЯРХМЮ, ЕЯКХ ЯОХЯНЙ ЖЕКЕБШУ СРБЕПФДЕМХИ
(ХУ ЙНМЗЧМЙЖХЪ) ХЯРХММЕМ Я РНВЙХ ГПЕМХЪ оПНЦП
кНЙЮКЭМШЕ ОЕПЕЛЕММШЕ:
жЕКЭ: ЖЕКЭ
дПСЦХЕжЕКХ: ЯОХЯНЙ ЖЕКЕИ
дНЯРХЦМСРШ: ХЯРХММНЯРМНЕ ГМЮВЕМХЕ
яНОНЯРЮБХКХЯЭ: ХЯРХММНЯРМНЕ ГМЮВЕМХЕ
йНМЙПЕР: ЙНМЙПЕРХГЮЖХЪ ОЕПЕЛЕММШУ
м, м', B1, B1', ..., бn , бn': ЖЕКХ
бЯОНЛНЦЮРЕКЭМШЕ ТСМЙЖХХ:
ОycРНИ( L): БНГБПЮЫЮЕР ХЯРХМС, ЕЯКХ L - ОСЯРНИ ЯОХЯНЙ
ЦНКoБa( L): БНГБПЮЫЮЕР ОЕПБШИ ЩКЕЛЕМР ЯОХЯЙЮ L
УБНЯР( L): БНГБПЮЫЮЕР НЯРЮКЭМСЧ ВЮЯРЭ ЯОХЯЙЮ L
ЙНМЙЮР( L1, L2): ЯНГДЮЕР ЙНМЙЮРЕМЮЖХЧ ЯОХЯЙНБ - ОПХЯНЕДХМЪЕР
ЯОХЯНЙ L2 Й ЙНМЖС ЯОХЯЙЮ L1
ЯНОНЯРЮБКЕМХЕ( T1, T2, яНОНЯРЮБХКХЯЭ, йНМЙПЕР): ОШРЮЕРЯЪ
ЯНОНЯРЮБХРЭ РЕПЛШ р1 Х T2; ЕЯКХ НМХ ЯНОНЯРЮБХЛШ, РН
яНОНЯРЮБХКХЯЭ - ХЯРХМЮ, Ю йНМЙПЕР ОПЕДЯРЮБКЪЕР
ЯНАНИ ЙНМЙПЕРХГЮЖХЧ ОЕПЕЛЕММШУ
ОНДЯРЮБХРЭ( йНМЙПЕР, жЕКХ): ОПНХГБНДХР ОНДЯРЮМНБЙС ОЕПЕЛЕММШУ
Б жЕКХ ЯНЦКЮЯМН йНМЙПЕР
begin
if ОСЯРНИ( яОХЯНЙжЕКЕИ) then сЯОЕУ : = ХЯРХМЮ
else
begin
жЕКЭ : = ЦНКНБЮ( яОХЯНЙжЕКЕИ);
дПСЦХЕжЕКХ : = УБНЯР( яОХЯНЙжЕКЕИ);
дНЯРХЦМСРЮ : = КНФЭ;
while not дНЯРХЦМСРЮ and
" Б ОПНЦПЮЛЛЕ ЕЯРЭ ЕЫЕ ОПЕДКНФЕМХЪ" do
begin
оСЯРЭ ЯКЕДСЧЫЕЕ ОПЕДКНФЕМХЕ Б оПНЦП ЕЯРЭ
м :- B1, .... бn.
яНГДЮРЭ БЮПХЮМР ЩРНЦН ОПЕДКНФЕМХЪ
м' :- б1', .... бn'.
ЯНОНЯРЮБКЕМХЕ( жЕКЭ, м',
яНОНЯРЮБХКХЯЭ, йНМЙПЕР)
if яНОНЯРЮБХКХЯЭ then
begin
мНБШЕжЕКХ : =
ЙНМЙЮР( [б1', ..., бn' ], дПСЦХЕ жЕКХ);
мНБШЕжЕКХ : =
ОНДЯРЮБХРЭ( йНМЙПЕР, мНБШЕжЕКХ);
БШВХЯКХРЭ( оПНЦП, мНБШЕжЕКХ, дНЯРХЦМСРШ)
end
end;
сЯОЕУ : = дНЯРХЦМСРШ
end
end;
line(); пХЯ. 2. 11. бШВХЯКЕМХЕ ЖЕКЕБШУ СРБЕПФДЕМХИ оПНКНЦЮ.
бЯЪЙХИ ПЮГ, ЙЮЙ ПЕЙСПЯХБМШИ БШГНБ ОПНЖЕДСПШ БШВХЯКХРЭ ОПХБНДЪР Й МЕСЯОЕУС, ОПНЖЕЯЯ БШВХЯКЕМХИ БНГБПЮЫЮЕРЯЪ Й опнялнрпс Х ОПНДНКФЮЕРЯЪ Я РНЦН ОПЕДКНФЕМХЪ я, ЙНРНПНЕ ХЯОНКЭГНБЮКНЯЭ ОНЯКЕДМХЛ. оНЯЙНКЭЙС ОПХЛЕМЕМХЕ ОПЕДКНФЕМХЪ я МЕ ОПХБЕКН Й СЯОЕЬМНЛС ГЮБЕПЬЕМХЧ, ОПНКНЦ-ЯХЯРЕЛЮ ДНКФМЮ ДКЪ ОПНДНКФЕМХЪ БШВХЯКЕМХИ ОНОПНАНБЮРЭ ЮКЭРЕПМЮРХБМНЕ ОПЕДКНФЕМХЕ.
б ДЕИЯРБХРЕКЭМНЯРХ ЯХЯРЕЛЮ ЮММСКХПСЕР ПЕГСКЭРЮРШ ВЮЯРХ БШВХЯКЕМХИ, ОПХБЕДЬХУ Й МЕСЯОЕУС, Х НЯСЫЕЯРБКЪЕР БНГБПЮР Б РС РНВЙС (ОПЕДКНФЕМХЕ я), Б ЙНРНПНИ ЩРЮ МЕСЯОЕЬМЮЪ БЕРБЭ МЮВХМЮКЮЯЭ. йНЦДЮ ОПНЖЕДСПЮ НЯСЫЕЯРБКЪЕР БНГБПЮР Б МЕЙНРНПСЧ РНВЙС, БЯЕ ЙНМЙПЕРХГЮЖХХ ОЕПЕЛЕММШУ, ЯДЕКЮММШЕ ОНЯКЕ ЩРНИ РНВЙХ, ЮММСКХПСЧРЯЪ. рЮЙНИ ОНПЪДНЙ НАЕЯОЕВХБЮЕР ЯХЯРЕЛЮРХВЕЯЙСЧ ОПНБЕПЙС ОПНКНЦ-ЯХЯРЕЛНИ БЯЕУ БНГЛНФМШУ ЮКЭРЕПМЮРХБМШУ ОСРЕИ БШВХЯКЕМХЪ ДН РЕУ ОНП, ОНЙЮ МЕ АСДЕР МЮИДЕМ ОСРЭ, БЕДСЫХИ Й СЯОЕУС, ХКХ ФЕ ДН РЕУ ОНП, ОНЙЮ МЕ НЙЮФЕРЯЪ, ВРН БЯЕ ОСРХ ОПХБНДЪР Й МЕСЯОЕУС.
лШ СФЕ ГМЮЕЛ, ВРН ДЮФЕ ОНЯКЕ СЯОЕЬМНЦН ГЮБЕПЬЕМХЪ ОНКЭГНБЮРЕКЭ ЛНФЕР ГЮЯРЮБХРЭ ЯХЯРЕЛС ЯНБЕПЬХРЭ БНГБПЮР ДКЪ ОНХЯЙЮ МНБШУ ПЕЬЕМХИ. б МЮЬЕЛ НОХЯЮМХХ ОПНЖЕДСПШ БШВХЯКХРЭ ЩРЮ ДЕРЮКЭ АШКЮ НОСЫЕМЮ.
йНМЕВМН, Б МЮЯРНЪЫХУ ПЕЮКХГЮЖХЪУ оПНКНЦЮ Б ОПНЖЕДСПС БШВХЯКХРЭ ДНАЮБКЕМШ Х ЕЫЕ МЕЙНРНПШЕ СЯНБЕПЬЕМЯРБНБЮМХЪ. нДМН ХГ МХУ - ЯНЙПЮЫЕМХЕ ПЮАНРШ ОН ОПНЯЛНРПЮЛ ОПНЦПЮЛЛШ Я ЖЕКЭЧ ОНБШЬЕМХЪ ЩТТЕЙРХБМНЯРХ. оНЩРНЛС МЮ ОПЮЙРХЙЕ ОПНКНЦ-ЯХЯРЕЛЮ МЕ ОПНЯЛЮРПХБЮЕР БЯЕ ОПЕДКНФЕМХЪ ОПНЦПЮЛЛШ, Ю БЛЕЯРН ЩРНЦН ПЮЯЯЛЮРПХБЮЕР РНКЭЙН РЕ ХГ МХУ, ЙНРНПШЕ ЙЮЯЮЧРЯЪ РЕЙСЫЕЦН ЖЕКЕБНЦН СРБЕПФДЕМХЪ.
Процесс рассуждений
Наш интерпретатор будет принимать вопрос и искать на него ответ. Язык правил допускает, чтобы в условной части правила была И / ИЛИ-комбинация условий. Вопрос на входе интерпретатора может быть такой же комбинацией подвопросов. Поэтому процесс поиска ответов на эти вопросы будет аналогичен процессу поиска в И / ИЛИ-графах, который мы обсуждали в гл. 13.
Ответ на заданный вопрос можно найти несколькими способами в соответствии со следующими принципами:
line();Для того, чтобы найти ответ Отв на вопрос В, используйте одну из следующих возможностей:
если В найден в базе знаний в виде факта, то Отв - это "В это правда"
если в базе знаний существует правило вида
"если Условие
то В",
то для получения ответа Отв рассмотрите Условие
если вопрос В можно задавать пользователю, спросите пользователя об истинности В
если в имеет вид В1 и В2, то рассмотрите В1, а затем,
если В1 ложно, то положите Отв равным "В
это ложь", в противном случае рассмотрите В2 и получите Отв
как соответствующую комбинацию ответов на вопросы В1 и В2
если В имеет вид В1 или В2, то рассмотрите В1, а затем,
если В1 истинно, то положите Отв равным "В1 это правда", в противном случае рассмотрите В2 и получите Oтв
как соответствующую комбинацию ответов на вопросы В1 и В2.
line();
Вопросы вида
не В
обрабатываются не так просто, и мы обсудим их позже.
Проект
Вообще говоря, задачи планирования характеризуются значительной комбинаторной сложностью. Наша простая эвристическая функция не обеспечивает высокой эффективности управления поиском. Предложите другие эвристические функции и проведите с ними эксперименты.
line();/* Отношения для задачи планирования.
Вершины пространства состояний - частичные планы,
записываемые как
[ Задача1/Т1, Задача2/Т2, ...]*
[ Задача1/К1, Задача2/К2, ...]* ВремяОкончания
В первом списке указываются ждущие задачи и продолжительности их выполнения; во втором - текущие решаемые задачи и их времена окончания, упорядоченные так, чтобы выполнялись неравенства K1<=K2, K2<=K3, ... . Время окончания плана - самое последнее по времени время окончания задачи.
*/
после( Задачи1*[ _ /К | Акт1]*Кон1, Задачи2*Акт2*Кон2,Ст):-
удалить( Задача/Т, Задачи1, Задачи2),
% Взять ждущую задачу
not( принадлежит( Здч1/_, Задачи2),
раньше( ЗДЧ, Задача) ),
% Проверить предшествование
Проект
Напишите программу для какой-нибудь простой игры (такой, как ним), использующую упрощенный алгоритм войска в И / ИЛИ-дереве.
Назад | Содержание | Вперёд
Проект
Рассмотрите какую-нибудь игру двух лиц (например, какой-нибудь нетривиальный вариант крестиков-ноликов). Напишите отношения, задающие правила этой игры (разрешенные ходы и терминальные позиции). Предложите статическую оценочную функцию, пригодную для использования в игровой программе, основанной на альфа-бета алгоритме.
Назад | Содержание | Вперёд
Проект
Рассмотрите какой-нибудь другой простой эндшпиль, например "король и пешка против короля", и напишите для него программу на языке AL0 (вместе с определениями соответствующих предикатов).
line();% Библиотека предикатов для окончания
% "король и ладья против короля"
% Позиция представлена стуктурой:
% ЧейХод..Бх : Бу..Лх : Лу..Чх : Чу..Глуб
% ЧейХод - с чьей стороны ход в этой позиции ('б' или 'ч')
% Бх, Бу - координаты белого короля
% Лх, Лу - координаты белой ладьи
% Чх, Чу - координаты черного короля
% Глуб - глубина, на которой находится эта позиция в дереве
% поиска
% Отношения выбора элементов позиции
чей_ход( ЧейХод.._, ЧейХод).
бк( _..БК.._, БК).
% Белый король
бл( _.._..БЛ.._, БЛ).
% Белая ладья
чк( _.._.._..ЧК.._, ЧК).
% Черный король
глуб( _.._.._.._..Глуб, Глуб).
восст_глуб( ЧХ..Б..Л..Ч..Г, ЧХ..Б..Л..Ч..0).
% Формируется копия позиции, глубина устанавливается в 0
% Некоторые отношения между клетками доски
Проект
Запрограммируйте интерпретатор, который, в соответствии с приведенным выше замечанием, реализует базу данных как аргумент пусковой процедуры и не использует для этого внутренней базы данных пролог-системы (т. е. обходится без assert и retract). Эта новая версия интерпретатора будет допускать автоматические возвраты. Попытайтесь разработать такое представление базы данных, которое облегчало бы сопоставление с образцами.
Проекты
Завершите программирование нашей оболочки в части, касающейся неопределенной информации (процедура ответпольз и другие).
Рассмотрите перечисленные выше критические замечания, а также возможные расширения нашей экспертной системы. Разработайте и реализуйте соответствующие усовершенствования.
представлением доски каждое решение
В соответствии с принятым в программе 1 представлением доски каждое решение имело вид
[1/Y1, 2/Y2, 3/Y3, ..., 8/Y8]
так как ферзи расставлялись попросту в последовательных вертикалях. Никакая информация не была бы потеряна, если бы Х-координаты были пропущены. Поэтому можно применить более экономное представление позиции на доске, оставив в нем только Y-координаты ферзей:
[Y1, Y2, Y3, ..., Y8]
Чтобы не было нападений по горизонтали, никакие два ферзя не должны занимать одну и ту же горизонталь. Это требование накладывает ограничение на Y-координаты: ферзи должны занимать все горизонтали с 1-й по 8-ю. Остается только выбрать порядок следования этих восьми номеров. Каждое решение представляет собой поэтому одну из перестановок списка:
[1, 2, 3, 4, 5, 6, 7, 8]
Такая перестановка S является решением, если каждый ферзь в ней не находится под боем (список S - "безопасный"). Поэтому мы можем написать:
решение( S) :-
перестановка( [1, 2, 3, 4, 5, 6, 7, 8], S),
безопасный( S).
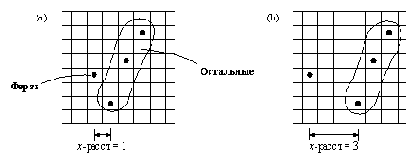
Рис. 4. 8. (а) Расстояние по Х между Ферзь и Остальные равно 1.
(b) Расстояние по Х между Ферзь и Остальные равно 3
Отношение перестановка мы уже определила в гл. 3, а вот отношение безопасный нужно еще определить. Это определение можно разбить на два случая:
(1) S - пустой список. Тогда он, конечно, безопасный, ведь нападать не на кого.
(2) S - непустой список вида [Ферзь | Остальные]. Он безопасный, если список Остальные - безопасный и Ферзь не бьет ни одного ферзя из списка Остальные.
На Прологе это выглядит так:
безопасный( [ ]).
безопасный( [Ферзь | Остальные ] :-
безопасный( Остальные),
небьет(Ферзь | Остальные).
В этой программе отношение небьет более хитрое.
line(); решение( Ферзи) :-
перестановка( [1, 2, 3, 4, 5, 6, 7, 8], Ферзи),
безопасный( Ферзи).
перестановка( [ ], [ ]).
перестановка( [Голова | Хвост], СписПер) :-
перестановка( Хвост, ХвостПер),
удалить( Голова, СписПер, ХвостПер).
% Вставка головы в переставленный хвост
удалить( А, [А | Список).
удалять( А, [В | Список], [В, Список1] ) :-
удалить( А, Список, Список1).
безопасный( [ ]).
безопасный( [Ферзь | Остальные]) :-
безопасный( Остальные),
небьет( Ферзь, Остальные, 1).
небьет( _, [ ], _ ).
небьет( Y, [Y1 | СписY], РасстХ) :-
Y1-Y =\= РасстХ,
Y-Y1 =\= РасстХ,
Расст1 is РасстХ + 1,
небьет( Y, СписY, Расст1).
line(); Рис. 4. 9. Программа 2 для задачи о восьми ферзях.
Трудность состоит в том, что расположение ферзей определяется только их Y-координатами, а Х-координаты в представлении позиции не присутствуют в явном виде. Этой трудности можно избежать путем небольшого обобщения отношения небьет, как это показано на рис. 4.8. Предполагается, что цель
небьет( Ферзь, Остальные)
обеспечивает отсутствие нападении ферзя Ферзь на поля списка Остальные в случае, когда расстояние по Х между Ферзь и Остальные равно 1.
Остается рассмотреть более общий случай произвольного расстояния. Для этого мы добавим его в отношение небьет в качестве третьего аргумента:
небьет( Ферзь, Остальные, РасстХ)
Соответственно и цель небьет в отношении безопасный должна быть изменена на
небьет( Ферзь, Остальные, 1)
Теперь отношение небьет может быть сформулировано в соответствии с двумя случаями, в зависимости от списка Остальные: если он пуст, то бить некого и, естественно, нет нападений; если же он не пуст, то Ферзь не должен бить первого ферзя из списка Остальные (который находится от ферзя Ферзь на расстоянии РасстХ вертикалей), а также ферзей из хвоста списка Остальные, находящихся от него на расстоянии РасстХ + 1. Эти соображения приводят к программе, изображенной на рис. 4.9.
Наша третья программа для задачи
Наша третья программа для задачи о восьми ферзях опирается на следующие соображения. Каждый ферзь должен быть размещен на некотором поле, т. е. на некоторой вертикали, некоторой горизонтали, а также на пересечении каких-нибудь двух диагоналей. Для того, чтобы была обеспечена безопасность каждого ферзя, все они должны располагаться в разных вертикалях, разных горизонталях и в разных диагоналях (как идущих сверху вниз, так и идущих снизу вверх). Естественно поэтому рассмотреть более богатую систему представления с четырьмя координатами:
x вертикали
у горизонтали
u диагонали, идущие снизу вверх
v диагонали, идущие сверху вниз
Эти координаты не являются независимыми: при заданных х и у, u и v определяются однозначно (пример на рис.4.10). Например,
u = х - у
v = х + у

Рис. 4. 10. Связь между вертикалями, горизонталями и диагоналями. Помеченное
поле имеет следующие координаты: x = 2, у = 4, u = 2 - 4 = -2, v = 2 + 4 = 6.
Области изменения всех четырех координат таковы:
Dx = [1, 2, 3, 4, 5, 6, 7, 8]
Dy = [1, 2, 3, 4, 5, 6, 7, 8]
Du = [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]
Dv = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
Задачу о восьми ферзях теперь можно сформулировать следующим образом: выбрать восемь четверок (X, Y, U, V), входящих в области изменения (X в Dx, Y в Dy и т.д.), так, чтобы ни один их элемент не выбирался дважды из одной области. Разумеется, выбор Х и Y определяет выбор U и V. Решение при такой постановке задачи может быть вкратце таким: при заданных 4-х областях изменения выбрать позицию для первого ферзя, вычеркнуть соответствующие элементы из 4-х областей изменения, а затем использовать оставшиеся элементы этих областей для размещения остальных ферзей.
Программа, основанная на таком подходе, показана на рис. 4.11. Позиция на доске снова представляется списком Y-координат. Ключевым отношением в этой программе является отношение
peш( СписY, Dx, Dy, Du, Dv)
которое конкретизирует Y-координаты (в СписY) ферзей, считая, что они размещены в последовательных вертикалях, взятых из Dx. Все Y-координаты и соответствующие координаты U и V берутся из списков Dy, Du и Dv. Главную процедуру решение можно запустить вопросом
?- решение( S)
Это вызовет запуск реш с полными областями изменения координат, что соответствует пространству
line(); решение( СписY) :-
реш( СписY, % Y-координаты ферзей
[1, 2, 3, 4, 5, 6, 7, 8],
% Область изменения Y-координат
[1, 2, 3, 4, 5, 6, 7, 8],
% Область изменения Х-координат
[-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7],
% Диагонали, идущие снизу вверх
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15, 14, 15, 16] ).
% Диагонали, идущие сверху вниз
реш([ ], [ ], Dy, Du, Dv).
реш( [Y | СписY], [X | Dx1], Dy, Du, Dv) :-
удалить( Y, Dy, Dy1), % Выбор Y-координаты
U is X-Y % Соответствующая диагональ вверх
удалить( U, Du, Du1), % Ее удаление
V is X+Y % Соответствующая диагональ вниз
удалить( V, Dv, Dv1), % Ее удаление
реш( СписY, Dх1, Dy1, Du1, Dv1).
% Выбор из оставшихся значений
удалить( А, [А | Список], Список).
удалить(A, [В | Список ], [В | Список1 ] ) :-
удалить( А, Список, Список1).
line(); Рис. 4. 11. Программа 3 для задачи о восьми ферзях.
задачи о восьми ферзях.
Процедура реш универсальна в том смысле, что ее можно использовать для решения задачи об N ферзях (на доске размером N х N). Нужно только правильно задеть области Dx, Dy и т.д.
Удобно автоматизировать получение этих областей. Для этого нам потребуется процедура
генератор( Nl, N2, Список)
которая для двух заданных целых чисел Nl и N2 порождает список
Список = [Nl, Nl + 1, Nl + 2, ..., N2 - 1, N2]
Вот она:
генератор( N, N, [N]).
генератор( Nl, N2, [Nl | Список]) :-
Nl < N2,
М is Nl + 1,
генератор( М, N2, Список).
Главную процедуру решение нужно соответствующим образом обобщить:
решение( N, S)
где N - это размер доски, а S - решение, представляемое в виде списка Y-координат N ферзей. Вот обобщенное отношение решение:
решение( N, S) :-
генератор( 1, N, Dxy),
Nu1 is 1 - N, Nu2 is N - 1,
генератор( Nu1, Nu2, Du),
Nv2 is N + N,
генератор( 2, Nv2, Dv),
реш( S, Dxy, Dxy, Du, Dv).
Например, решение задачи о 12 ферзях будет получено с помощью:
?- решение( 12, S).
S = [1, 3, 5, 8, 10, 12, 6, 11, 2, 7, 9, 4]
Программа на языке AL для игры в шахматном эндшпиле
При реализации какой-либо игровой программы на языке AL0 ее можно для удобства разбить на три модуля:
(1) интерпретатор языка AL0,
(2) таблица советов на языке AL0,
(3) библиотека предикатов, используемых в таблице советов (в том числе
предикаты, задающие правила игры).
Эта структура соответствует обычной структуре системы, основанной на знаниях:
Интерпретатор AL0 выполняет функцию машины логического вывода.
Таблица советов вместе с библиотекой предикатов образует базу знаний.
Программа на языке советов для эндшпиля "король и ладья против короля"
Общий принцип достижения выигрыша королем и ладьей против единственной фигуры противника, короля, состоит в том, чтобы заставить короля отступить к краю доски или, при необходимости, загнать его в угол, а затем поставить мат в несколько ходов. В детальном изложении эта стратегия выглядит так:
line();Повторять циклически, пока не будет поставлен мат (постоянно проверяя, что не возникла патовая позиция и что нет нападения на незащищенную ладью):
(1) Найти способ поставить королю противника мат в два хода.
(2) Если не удалось, то найти способ уменьшить ту область доски, в которой
король противника "заперт" под воздействием ладьи.
(3) Если и это не удалось, то найти способ приблизить своего короля к королю
противника.
(4) Если ни один из элементарных советов 1, 2, или 3 не выполним, то найти
способ сохранить все имеющиеся к настоящему моменту "достижения" в
смысле (2) и (3) (т. е. сделать выжидающий ход).
(5) Если ни одна из целей 1, 2, 3 или 4 не достижима, то найти способ получить
позицию, в которой ладья занимает вертикальную или горизонтальную
линию, отделяющую одного короля от другого.
Описанные выше принципы реализованы во всех деталях в таблице советов на языке AL0, показанной на рис. 15.7.
Эта таблица может работать под управлением интерпретатора рис. 15.6. Рис. 15.8 иллюстрирует смысл некоторых из предикатов, использованных в таблице советов, а также показывает, как эта таблица работает.
В таблице используются следующие предикаты:
Предикаты целей
мат
мат королю противника
пат
пат королю противника
потеря_ладьи
король противника может взять ладью
ладья_под_боем
король противника может напасть на ладью прежде, чем наш
король сможет ее защитить
уменьш_простр
уменьшилось "жизненное пространство" короля противника,
ограничиваемое ладьей
раздел
ладья занимает вертикальную или горизонтальную линию,
разделяющую королей
ближе_к_клетке наш король приблизился к "критической клетке" (см. рис. 15.9),
т.е. манхеттеновское расстояние до нее уменьшилось
l_конфиг "L-конфигурация" (рис. 15.9)
простр_больше_2 "жизненное пространство" короля противника занимает
больше двух клеток
Предикаты, ограничивающие ходы
глубина = N
ход на глубине N дерева поиска
разреш
любой разрешенный ход
ход_шах
ход, объявляющий шах
ход_ладьей
ход ладьей
нет_хода
ни один ход не подходит
сначала_диаг
ход королем, преимущественно по диагонали
line();
% Окончание "король и ладья против короля" на языке AL0
% Правила
правило_края:
если король_противника_на_краю и короли_рядом
то [мат_2, потеснить, приблизиться,
сохранить_простр, отделить_2, отделить_3].
иначе_правило
если любая_поз
то [ потеснить, приблизиться, сохранить_простр,
отделить_2, отделить_3].
% Элементарные советы
совет( мат_2,
мат :
не потеря_ладьи и король_противника_на_краю:
(глубина = 0) и разреш
затем (глубина = 2) и ход_шах :
(глубина = 1) и разреш ).
совет( потеснить,
уменьш_простр и не ладья_под_боем и
раздел и не пат :
не потеря_ладьи :
(глубина = 0) и ход_ладьей :
нет_хода ).
совет( приблизиться,
ближе _к_клетке и не ладья_под_боем и
(раздел или l_конфиг) и
(простр_больше_2 или не наш_король_на_краю):
не потеря_ладьи :
(глубина = 0) и сначала_диаг :
нет_хода ).
совет( сохранить_простр,
ход_противиика и не ладья_под_боем и раздел
и не_дальше_от_ладьи и
(простр_больше_2 или не наш_король_на_краю):
не потеря_ладьи :
(глубина = 0) и сначала_диаг :
нет_хода ).
совет( отделить_2,
ход_противника и раздел и не ладья_под_боем:
не потеря_ладьи :
(глубина < 3) и разреш :
(глубина < 2) и разреш ).
совет( отделить_3,
ход_противника и раздел и не ладья_под_боем:
не потеря_ладьи :
(глубина < 5) и разреш :
(глубина < 4) и разреш ).
line();
Рис. 15. 7. Таблица советов на языке AL0 для окончания "король
и ладья против короля". Таблица состоит из двух правил и шести
элементарных советов.
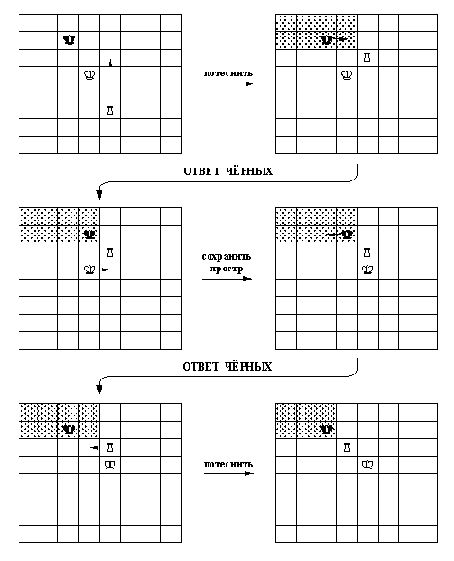
Рис. 15. 8. Фрагмент шахматной партии, полученный с использованием
таблицы советов рис. 15.7 и иллюстрирующий применение стратегии
оттеснения короля в угол доски. В этой последовательности ходов
выполнялись элементарные советы: сохранить_ простр (выжидающий
ход, сохраняющий "жизненное пространство" черного короля) и
потеснить (ход, сокращающий "жизненное пространство"). Область,
в которой заключен черный король, выделена штриховкой. После
выполнения последнего совета потеснить эта область сократилась
с восьми до шести клеток.

Рис. 15. 9. (а) "Критическая клетка" отмечена крестиком. Она
используется при маневрировании с целью оттеснить черного
короля. Белый король приближается к "критической клетке",
двигаясь, как указано на рисунке. (б) Три фигуры образуют
конфигурацию, напоминающую букву L.
Аргументами этих предикатов являются либо позиции (в предикатах целей), либо ходы (в предикатах, ограничивающих ходы). Предикаты целей могут иметь один или два аргумента. Первый из аргументов - это всегда текущая вершина поиска; второй аргумент (если он имеется) - корневая вершина дерева поиска. Второй аргумент необходим в так называемых сравнивающих предикатах, которые сравнивают корневую и текущую позиции в том или ином отношении. Например, предикат уменьш_простр проверяет, сократилось ли "жизненное пространство" короля противника (рис. 15.8). Эти предикаты вместе с шахматными правилами (применительно к окончанию "король и ладья против короля"), а также процедура для отображения текущего состояния игровой доски ( отобр ( Поз) ) запрограммированы на рис. 15.10.
На рис. 15.8 показано, как играет наша программа, основанная на механизме советов. При продолжении игры из последней позиции рис. 15.8 она могла бы протекать так, как в приведенном ниже варианте (в предположении, что "противник" ходит именно так, как указано). Здесь использована алгебраическая шахматная нотация, в которой вертикальные линии пронумерованы, как 'а', 'b', 'с', .... а горизонтальные - как 1, 2, 3, ... .
Например, ход ЧК b7 означает: передвинуть черного короля на клетку. расположенную на пересечении вертикальной линии 'b' с горизонтальной линией 7.
... ЧК b7
БК d5 ЧК с7
БК с5 ЧК b7
БЛ с6 ЧК а7
БЛ b6 ЧК а8
БК b5 ЧК а7
БК с6 ЧК а8
БК с7 ЧК а7
БЛ с6 ЧК а8
БЛ а6 мат
Теперь уместно задать некоторые вопросы. Во-первых, является ли наша программа-советчик корректной в том смысле, что она ставит мат при любом варианте защиты со стороны противника и при любой начальной позиции, в которой на доске король и ладья против короля? В статье Bratko (1978) приведено формальное доказательство того, что таблица советов, практически совпадающая с таблицей рис. 15.7, действительно является корректной в указанном смысле.
Другой возможный вопрос: является ли программа оптимальной, то есть верно ли, что она ставит мат за минимальное число ходов? Нетрудно показать на примерах, что игру нашей программы в этом смысле нельзя назвать оптимальной.Известно, что оптимальный вариант в этом окончании (т.е. предполагающий оптимальную игру с обеих сторон) имеет длину не более 16 ходов. Хотя наша таблица советов и далека от этого оптимума, было показано, что число, ходов наверняка не превосходит 50. Это важный результат в связи с тем, что в шахматах существует "правило 50-ти ходов": в эндшпилях типа "король и ладья против короля" противник, имеющий преимущество, должен поставить, мат не более, чем за 50 ходов; иначе может быть объявлена ничья.
Программа поиска
Программа, в которой реализованы идеи предыдущего раздела, показана на рис. 13.12. Прежде, чем мы перейдем к объяснению отдельных деталей этой программы, давайте рассмотрим тот способ представления дерева поиска, который в ней используется.
Существует несколько случаев, как показано на рис. 13.11. Различные формы представления поискового дерева возникают как комбинации следующих возможных вариантов, относящихся к размеру дерева и к его "решающему статусу".
Размер:
(1) дерево состоит из одной вершины (листа)
или
(2) оно имеет корень и (непустые) поддеревья.
Решающий статус:
(1) обнаружено, что дерево соответствует
решению задачи( т. е. является решающим
деревом) или
(2) оно все еще решающее дерево-кандидат.
Основной функтор, используемый для представления дерева, указывает, какая из комбинаций этих воз-
line();
Рис. 13. 11. Представление дерева поиска.
можностей имеется в виду. Это может быть одна из следующих комбинаций:
лист решлист дер решдер
Далее, в представление дерева входят все или некоторые из следующих объектов: корневая вершина дерева, F-оценка дерева, стоимость С дуги И / ИЛИ-графа, ведущей в корень дерева, список поддеревьев, отношение (И или ИЛИ) между поддеревьями.
Список поддеревьев всегда упорядочен по возрастанию F-оценок. Поддеревья, являющиеся решающими деревьями, помещаются в конец списка.
Обратимся теперь к программе рис. 13.12. Отношение самого высокого уровня - это
и_или( Верш, РешДер)
где Верш - стартовая вершина. Программа строит решающее дерево (если таковое существует), рассчитывая на то, что оно окажется оптимальным решением. Будет ли это решение в действительности самым дешевым, зависит от той функции h, которую использует алгоритм.
Существует теорема, в которой говорится о том, как оптимальность решения зависит от h. Эта теорема аналогична теореме о допустимости алгоритма поиска с предпочтением в пространстве состояний (гл. 12). Обозначим через С( В) стоимость оптимального решающего дерева для вершины В. Если для каждой вершины В И / ИЛИ-графа эвристическая оценка h( B) <= C( B), то гарантируется, что процедура и_или
найдет оптимальное решение. Если же h
не удовлетворяет этому условию, то найденное решение может оказаться субоптимальным. Существует тривиальная эвристическая функция, удовлетворяющая условию оптимальности, а именно h = 0 для всех вершин. Ее недостатком является отсутствие эвристической силы.
Основную роль в программе рис. 13.12 играет отношение
расширить( Дер, Предел, Дер1, ЕстьРеш)
Дер и Предел - его "входные" аргументы, а Дер1 и ЕстьРеш
- "выходные". Аргументы имеют следующий смысл:
Дер - дерево поиска, подлежащее расширению.
Предел - предельное значени F-оценки, при котором еще разрешено наращивать дерево Дер.
ЕстьРеш - индикатор, значения которого указывают на то, какой из следующих трех случаев имеет место:
(1) ЕстьРеш = да: Дер можно "нарастить" (с учетом ограничения Предел) таким образом, чтобы образовалось решающее дерево Дер1.
(2) ЕстьРеш = нет: дерево Дер можно расширить до состояния Дер1, для которого F-оценка превосходит Предел, но прежде чем F-оценка превзошла Предел, решающее дерево не было обнаружено.
(3) ЕстьРеш = никогда: Дер не содержит решения.
В зависимости от случая Дер1 - это либо решающее дерево, либо Дер, расширенное до момента перехода через Предел; если ЕстьРеш = никогда, то переменная Дер1
неинициализирована.
Процедура
расширспис( Деревья, Предел, Деревья1, ЕстьРеш)
аналогична процедуре расширить. Так же, как и в процедуре расширить, Предел
задает ограничение на рост дерева, а ЕстьРеш
- это индикатор, указывающий, каков результат расширения ("да", "нет" или "никогда"). Первый аргумент - это, на этот раз, список деревьев (И-список или ИЛИ-список):
Деревья = или:[Д1, Д2, ...] или
Деревья = и : [Д1, Д2, ...]
Процедура расширспис выбирает из списка Деревья наиболее перспективное дерево (исходя из F-оценок). Так как деревья в списке упорядочены, таким деревом является первый элемент списка. Наиболее перспективное дерево подвергается расширению с новым ограничением Предел1. Значение Предел1
зависит от Предел, а также от других деревьев списка. Если Деревья - это ИЛИ-список, то Предел1 устанавливается как наименьшая из двух величин: Предел и F-оценка следующего по "качеству" дерева из списка Деревья. Если Деревья
- это И-дерево, то Предел1
устанавливается равным Предел минус сумма F-оценок всех остальных деревьев из списка. Значение переменной Деревья1
зависит от случая, задаваемого индикатором ЕстьРеш. Если ЕстьРеш = нет, то Деревья1 - это то же самое, что и список Деревья, причем наиболее перспективное дерево расширено с учетом ограничения Предел1. Если ЕстьРеш = да, то Деревья1 - это решение для всего списка Деревья (найденное без выхода за границы значения Предел). Если ЕстьРеш = никогда, то переменная Деревья1
неинициализирована.
Процедура продолжить, вызываемая после расширения списка деревьев, решает, что делать дальше, в зависимости от результата срабатывания процедуры расширить. Эта процедура либо строит решающее дерево, либо уточняет дерево поиска и продолжает процесс его наращивания, либо выдает сообщение "никогда" в случае, когда было обнаружено, что список деревьев не содержит решения.
line();
/* ПРОГРАММА И / ИЛИ-ПОИСКА С ПРЕДПОЧТЕНИЕМ
Эта программа порождает только одно решение. Гарантируется, что это решение самое дешевое при условии, что используемая эвристическая функция является нижней гранью реальной стоимости решающих деревьев.
Дерево поиска имеет одну из следующих форм:
дер( Верш, F, С, Поддеревья) дерево-кандидат
лист( Верш, F, C) лист дерева поиска
решдер( Верш, F, Поддеревья) решающее дерево
решлист( Верш, F) лист решающего дерева
С - стоимость дуги, ведущей в Верш
F = С + Н, где Н - эвристическая оценка оптимального решающего дерева с корнем Верш
Список Поддеревья упорядочен таким образом, что
(1) решающие поддеревья находятся в конце списка;
(2) остальные поддеревья расположены в порядке возрастания F-оценок
*/
:- ор( 500, xfx, :).
:- ор( 600, xfx, --->).
и_или( Верш, РешДер) :-
расширить( лист( Верш, 0, 0), 9999, РешДер, да).
% Предполагается, что 9999 > любой F-оценки
% Процедура расширить( Дер, Предел, НовДер, ЕстьРеш)
% расширяет Дер в пределах ограничения Предел
% и порождает НовДер с "решающим статусом" ЕстьРеш.
% Случай 1: выход за ограничение
расширить( Дер, Предел, Дер, нет) :-
f( Дер, F), F > Предел, !.
% Выход за ограничение
% В остальных случаях F <= Предел
% Случай 2: встретилась целевая вершина
расширить( лист( Верш, F, С), _, решлист( Верш, F), да) : -
цель( Верш), !.
% Случай 3: порождение преемников листа
расширить( лист( Верш, F,C), Предел, НовДер, ЕстьРеш) :-
расшлист( Верш, С, Дер1), !,
расширить( Дер1, Предел, НовДер, ЕстьРеш);
ЕстьРеш = никогда, !.
% Нет преемников, тупик
% Случай 4: расширить дерево
расширить( дер( Верш, F, С, Поддеревья),
Предел, НовДер, ЕстьРеш) :-
Предел1 is Предел - С,
расширспис( Поддеревья, Предел1, НовПоддер, ЕстьРеш1),
продолжить( ЕстьРеш1, Верш, С, НовПоддер, Предел,
НовДер, ЕстьРеш).
% расширспис( Деревья, Предел, Деревья1, ЕстьРеш)
% расширяет деревья из заданного списка с учетом
% ограничения Предел и выдает новый список Деревья1
% с "решающим статусом" ЕстьРеш.
расширспис( Деревья, Предел, Деревья1, ЕстьРеш) :-
выбор( Деревья, Дер, ОстДер, Предел, Предел1),
расширить( Дер, Предел1, НовДер, ЕстьРеш1),
собрать( ОстДер, НовДер, ЕстьРеш1, Деревья1, ЕстьРеш).
% "продолжить" решает, что делать после расширения
% списка деревьев
продолжить( да, Верш, С, Поддеревья, _,
решдер( Верш, F, Поддеревья), да): -
оценка( Поддеревья, Н), F is С + H, !.
продолжить( никогда, _, _, _, _, _, никогда) :- !.
продолжить( нет, Верш, С, Поддеревья, Предел,
НовДер, ЕстьРеш) :-
оценка( Поддеревья, Н), F is С + Н, !,
расширить( дер( Верш, F, С, Поддеревья), Предел,
НовДер, ЕстьРеш).
% "собрать" соединяет результат расширения дерева со списком деревьев
собрать( или : _, Дер, да, Дер, да):- !.
% Есть решение ИЛИ-списка
собрать( или : ДД, Дер, нет, или : НовДД, нет) :-
встав( Дер, ДД, НовДД), !.
% Нет решения ИЛИ-списка
собрать( или : [ ], _, никогда, _, никогда) :- !.
% Больше нет кандидатов
собрать( или:ДД, _, никогда, или:ДД, нет) :- !.
% Есть еще кандидаты
собрать( и : ДД, Дер, да, и : [Дер Э ДД], да ) :-
всереш( ДД), !.
% Есть решение И-списка
собрать( и : _, _, никогда, _, никогда) :- !.
% Нет решения И-списка
собрать( и : ДД, Дер, ДаНет, и : НовДД, нет) :-
встав( Дер, ДД, НовДД), !.
% Пока нет решения И-списка
% "расшлист" формирует дерево из вершины и ее преемников
расшлист( Верш, С, дер( Верш, F, С, Оп : Поддеревья)) :-
Верш---> Оп : Преемники,
оценить( Преемники, Поддеревья),
оценка( Оп : Поддеревья, Н), F is С + Н.
оценить( [ ], [ ]).
оценить( [Верш/С | ВершиныСтоим], Деревья) :-
h( Верш, Н), F is С + Н,
оценить( ВершиныСтоим, Деревья1),
встав( лист( Верш, F, С), Деревья1, Деревья).
% "всереш" проверяет, все ли деревья в списке "решены"
всереш([ ]).
всереш( [Дер | Деревья] ) :-
реш( Дер),
всереш( Деревья).
реш( решдер( _, _, _ ) ).
реш( решлист( _ , _) ).
f( Дер, F) :-
% Извлечь F-оценку дерева
arg( 2, Дер, F), !.
% F - это 2-й аргумент Дер
% встав( Дер, ДД, НовДД) вставляет Дер в список
% деревьев ДД; результат - НовДД
встав( Д, [ ], [Д] ) :- !.
встав( Д, [Д1 | ДД], [Д, Д1 | ДД] ) :-
реш( Д1), !.
встав( Д, [Д1 | ДД], [Д1 | ДД1] ) :-
реш( Д),
встав( Д, ДД, ДД1), !.
встав( Д, [Д1 | ДД], [Д, Д1 | ДД] ) :-
f( Д, F), f( Д1, F1), F=< F1, !.
встав( Д, [Д1 | ДД], [ Д1 | ДД1] ) :-
встав( Д, ДД, ДД1).
% "оценка" находит "возвращенную" F-оценку И / ИЛИ-списка деревьев
оценка( или :[Дер | _ ], F) :-
% Первое дерево ИЛИ-списка - наилучшее
f( Дер, F), !.
оценка( и :[ ], 0) :- !.
оценка( и : [Дер1 | ДД], F) :-
f( Дер1, F1),
оценка( и : ДД, F2),
F is F1 + F2, !.
оценка( Дер, F) :-
f( Дер, F).
% Отношение выбор( Деревья, Лучшее, Остальные, Предел, Предел1):
% Остальные - И / ИЛИ-список Деревья без его "лучшего" дерева
% Лучшее; Предел - ограничение для Списка Деревья, Предел1 -
% ограничение для дерева Лучшее
выбор( Оп : [Дер], Дер, Оп : [ ], Предел, Предел) :- !.
% Только один кандидат
выбор( Оп : [Дер | ДД], Дер, Оп : ДД, Предел, Предел1) :-
оценка( Оп : ДД, F),
( Оп = или, !, мин( Предел, F, Предел1);
Оп = и, Предел1 is Предел - F).
мин( А, В, А) :- А < В, !.
мин( А, В, В).
line();
Рис. 13. 12. Программа поиска с предпочтением в И / ИЛИ-графе.
Еще одна процедура
собрать( ОстДер, НовДер, ЕстьРеш1, НовДеревья, ЕстьРеш)
связывает между собой несколько объектов, с которыми работает расширспис. НовДер
- это расширенное дерево, взятое из списка деревьев процедуры расширспис, ОстДер
- остальные, не измененные деревья из этого списка, а ЕстьРеш1 указывает на "решающий статус" дерева НовДер. Процедура собрать имеет дело с несколькими случаями в зависимости от значения ЕстьРеш1, а также от того, является ли список деревьев И-списком или ИЛИ-списком. Например, предложение
собрать( или : _, Дер, да, Дер, да).
означает: в случае, когда список деревьев - это ИЛИ-список и при только что проведенном расширении получено решающее дерево, считать, что задача, соответствующая всему списку деревьев, также решена, а ее решающее дерево и есть само дерево Дер. Остальные случаи легко понять из текста процедуры собрать.
Для отображения решающего дерева можно определить процедуру, аналогичную процедуре отобр
(рис. 13.8). Оставляем это читателю в качестве упражнения.
Программирование на языке Пролог для искусственного интеллекта
Перевод с английского.
Москва, "МИР", 1990 подробнее...
Электронную версию книги создал Иванов Виктор Михайлович. Книга размещена на сайте http://dstu2204.narod.ru/ ( на этой странице ).
ПРОГРАММИРОВАНИЕ В ТЕРМИНАХ ТИПОВЫХ КОНФИГУРАЦИЙ
В этой главе мы будем заниматься системами, ориентированными на типовые конфигурации ("образцы"), рассматривая их как некоторый специальный подход к программированию. Языком, ориентированным на образцы, можно считать и сам Пролог. Мы реализуем небольшой интерпретатор для простых программ этого типа и постараемся передать дух такого "конфигурационной" программирования на нескольких примерах.
double_line();Прологовские программы как системы, управляемые образцами
Программы, написанные на Прологе, можно рассматривать как системы, управляемые образцами. Между пролог-программами и этими системами можно установить соответствие примерно следующим образом: Каждое предложение прологовской программы можно считать отдельным модулем со своим пусковым образцом. Голова предложения соответствует образцу, тело - тому действию, которое выполняет модуль. База данных системы - это текущий список целей, которые пролог-система пытается удовлетворить. Предложение пролог-системы "запускается", если его голова сопоставима с целью, расположенной первой в базе данных. Выполнить действие модуля (т.е. тело предложе ния) - это значит: поместить в базу данных вместо первой из целей весь список целей тела предложения (с соответствующей конкретизацией переменных). Процесс активизации модулей (предложений) не детерминирован в том смысле, что с первой целью базы данных могут удачно сопоставить свою голову сразу несколько предложений, и, вообще говоря, любое из них может быть запущено. В Прологе этот недетерминизм реализован при помощи механизма возвратов.

Рис. 16. 2. Основной цикл работы системы, управляемой образцами.
В этом примере база данных согласуется с пусковыми образцами
модулей 1, 3 и 4; для выполнения выбран модуль 3.
Простая программа для автоматического докаэательства теорем
В настоящем разделе мы реализуем простую программу для автоматического доказательства теорем в виде системы, управляемой образцами. Эта программа будет основана на принципе резолюции - популярном методе, обычно используемом в машинном доказательстве теорем. Мы ограничимся случаем пропозициональной логики, поскольку нашей целью будет дать всего лишь простую иллюстрацию используемого принципа. На самом деле, принцип резолюции можно легко обобщить на случай исчисления высказываний первого порядка (с применением логических формул, содержащих переменные). Базовый Пролог можно рассматривать как частный случай системы доказательства теорем, основанной на принципе резолюции.
Задачу доказательства теорем можно сформулировать так: дана формула, необходимо показать, что эта формула является теоремой, т. е. она верна всегда, независимо от интерпретации встречающихся в ней символов. Например, утверждение, записанное в виде формулы
р v ~ р
и означающее "р или не р", верно всегда, независимо от смысла утверждения р.
Мы будем использовать в качестве операторов следующие символы:
~ отрицание, читается как "не"
& конъюнкцию, читается как "и"
v дизъюнкцию, читается как "или"
=> импликацию, читается как "следует"
Согласно правилам предпочтения операторов, оператор "не" связывает утверждения сильнее, чем "и", "или" и "следует".
Метод резолюции предполагает, что мы рассматриваем отрицание исходной формулы и пытаемся показать, что полученная формула противоречива. Если это действительно так, то исходная формула представляет собой тавтологию.
Таким образом, основную идею можно сформулировать так: доказательство противоречивости формулы с отрицанием эквивалентно доказательству того, что исходная формула (без отрицания) есть теорема (т. е. верна всегда). Процесс, приводящий к искомому противоречию, состоит из отдельных шагов, на каждом из которых применяется резолюция.
Давайте проиллюстрируем этот принцип на примере. Предположим, что мы хотим доказать, что теоремой является следующая пропозициональная формула:
(а => b) & (b => с) => (а => с)
Смысл этой формулы таков: если из а следует b и из b следует с, то из а следует с.
Прежде чем начать применять процесс резолюции ("резолюционный процесс"), необходимо представить отрицание нашей формулы в наиболее приспособленной для этого форме. Такой формой является конъюнктивная нормальная форма, имеющая вид
(р1 v p2
v ...) & (q1 v q2
v ...)
& (r1 v r2 v ...) & ...
Здесь рi, qi, ri
- элементарные утверждения или их отрицания. Конъюнктивная нормальная форма есть конъюнкция членов, называемых дизъюнктами, например (p1 v p2
v ...) - это дизъюнкт.
Любую пропозициональную формулу нетрудно преобразовать в такую форму. В нашем случае это делается следующим образом. У нас есть исходная формула
(а => b) & (b => с) => (а => с)
Ее отрицание имеет вид
~ ( (а => b) & (b => с) => (а => с) )
Для преобразования этой формулы в конъюнктивную нормальную форму можно использовать следующие известные правила:
(1) х => у
эквивалентно ~х v у
(2) ~(x
v y) эквивалентно ~х & ~у
(3) ~(х
& у) эквивалентно ~х v ~у
(4) ~( ~х) эквивалентно х
Применяя правило 1, получаем
~ ( ~ ( (a => b) & (b => с)) v (а => с) )
Далее, правила 2 и 4 дают
(а => b) & (b => с) & ~(а => с)
Трижды применив правило 1, получаем
(~ а v b) & (~b v с) & ~(~а
v с)
И наконец, после применения правила 2 получаем искомую конъюнктивную нормальную форму
(~а v b) & (~b v с) & а
& ~с
состоящую из четырех дизъюнктов. Теперь можно приступить к резолюционному процессу.
Элементарный шаг резолюции выполняется всегда, когда имеется два дизъюнкта, в одном из которых встретилось элементарное утверждение р, а в другом - ~р. Пусть этими двумя дизъюнктами будут
р v Y
и ~р v Z
Шаг резолюции порождает третий дизъюнкт:
Y v Z
Нетрудно показать, что этот дизъюнкт логически следует из тех двух дизъюнктов, из которых он получен. Таким образом, добавив выражение (Y
v Z) к нашей исходной формуле, мы не изменим ее истинности. Резолюционный процесс порождает новые дизъюнкты. Появление "пустого дизъюнкта" (обычно записываемого как "nil") сигнализирует о противоречии. Действительно, пустой дизъюнкт nil порождается двумя дизъюнктами вида
x и ~x
которые явно противоречат друг другу.

Рис. 16. 6. Доказательство теоремы (а=>b)&(b=>с)=>(a=>с) методом
резолюции. Верхняя строка - отрицание теоремы в конъюнктивной
нормальной форме. Пустой дизъюнкт внизу сигнализирует, что
отрицание теоремы противоречиво.
На рис. 16.6 показан процесс применения резолюций, начинающийся с отрицания нашей предполагаемой теоремы и заканчивающийся пустым дизъюнктом.
На рис. 16.7 мы видим, как резолюционный процесс можно сформулировать в форме программы, управляемой образцами. Программа работает с дизъюнктами, записанными в базе данных.
В терминах образцов принцип резолюции формулируется следующим образом:
если
существуют два таких дизъюнкта С1 и С2, что
P является (дизъюнктивным) подвыражением С1,
а ~Р - подвыражением С2
то
удалить Р из С1 (результат - СА), удалить ~Р
из С2 (результат - СВ) и добавить в базу
данных новый дизъюнкт СА v СВ.
На нашем формальном языке это можно записать так:
[ дизъюнкт( С1), удалить( Р, Cl, CA),
дизъюнкт( С2), удалить( ~Р, С2, СВ) ] --->
[ assert( дизъюнкт( СА v СВ) ) ].
Это правило нуждается в небольшой доработке. Дело в том, что мы не должны допускать повторных взаимодействий между дизъюнктами, так как они порождают новые копии уже существующих формул. Для этого в программе рис. 16.7 предусматривается запись в базу данных информации об уже произведенных взаимодействиях в форме утверждений вида
сделано( Cl, C2, Р)
В условных частях правил производится распознавание подобных утверждений и обход соответствующих повторных действий.
Правила, показанные на рис. 16.7, предусматривают также обработку специальных случаев, в которых требуется избежать явного представления пустого дизъюнкта. Кроме того, имеются два правила для упрощения дизъюнктов. Одно из них убирает избыточные подвыражения. Например, это правило превращает выражение
a v b v a
в более простое выражение a v b. Другое правило распознает те дизъюнкты, которые всегда истинны, например,
a v b v ~а
и удаляет их из базы данных, поскольку они бесполезны при поиске противоречия.
line(); % Продукционные правила для задачи автоматического
% доказательства теорем
% Противоречие
[ дизъюнкт( X), дизъзюнкт( ~Х) ] --->
[ write( 'Обнаружено противоречие'), стоп].
% Удалить тривиально истинный дизъюнкт
[ дизъюнкт( С), внутри( Р, С), внутри( ~Р, С) ] --->
[ retract( С) ].
% Упростить дизъюнкт
[ дизъюнкт( С), удалить( Р, С, С1), внутри( Р, С1) ] --->
[ заменить( дизъюнкт( С), дизъюнкт( С1) ) ].
% Шаг резолюции, специальный случай
[ дизъюнкт( Р), дизъюнкт( С), удалить( ~Р, С, С1),
not сделано( Р, С, Р) ] --->
[ аssеrt( дизъюнкт( С1)), аssert( сделано( Р, С, Р))].
% Шаг резолюции, специальный случай
[ дизъюнкт( ~Р), дизъюнкт( С), удалить( Р, С, С1),
not сделано( ~Р, С, Р) ] --->
[ assert( дизъюнкт( C1)), аssert( сделано( ~Р, С, Р))].
% Шаг резолюции, общий случай
[ дизъюнкт( С1), удалить( Р, С1, СА),
дизъюнкт( С2), удалить( ~Р, С2, СВ),
not сделано( Cl, C2, Р) ] --->
[ assert( дизъюнкт( СА v СВ) ),
assert( сделано( Cl, C2, Р) ) ].
% Последнее правило: тупик
[ ] ---> [ write( 'Нет противоречия'), стоп ].
% удалить( Р, Е, Е1) означает, получить из выражения Е
% выражение Е1, удалив из него подвыражение Р
удалить( X, X v Y, Y).
удалить( X, Y v X, Y).
удалить( X, Y v Z, Y v Z1) :-
удалить( X, Z, Z1).
удалить( X, Y v Z, Y1 v Z) :-
удалить( X, Y, Y1).
% внутри( Р, Е) означает Р есть дизъюнктивное подвыражение
% выражения Е
внутри( X, X).
внутри( X, Y) :-
удалить( X, Y, _ ).
line(); Рис. 16. 7. Программа, управляемая образцами, для
автоматического доказательства теорем.
Остается еще один вопрос: как преобразовать заданную пропозициональную формулу в конъюнктивную нормальную форму? Это несложное преобразование выполняется с помощью программы, показанной на рис. 16.8.
Процедура
транс( Формула)
транслирует заданную формулу в множество дизъюнктов Cl, C2 и т.д. и записывает их при помощи assert в базу данных в виде утверждений
дизъюнкт( С1).
дизъюнкт( С2).
. . .
Программа, управляемая образцами, для автоматического доказательства теорем запускается при помощи цели пуск. Таким образом, для того чтобы доказать при помощи этой программы некоторую теорему, мы транслируем ее отрицание в конъюнктивную нормальную форму, а затем запускаем резолюционный процесс. В нашем примере это можно сделать так:
line(); % Преобразование пропозициональной формулы в множество
% дизъюнктов с записью их в базу данных при помощи assert
:- ор( 100, fy, ~). % Отрицание
:- ор( 110, xfy, &). % Конъюнкция
:- ор( 120, xfy, v). % Дизъюнкция
:- ор( 130, xfy, =>). % Импликация
транс( F & G) :- !, % Транслировать конъюнктивную формулу
транс( F),
транс( G).
транс( Формула) :-
тр( Формула, НовФ), !, % Шаг трансформации
транс( НовФ).
транс( Формула) :- % Дальнейшая трансформация невозможна
assert( дизъюнкт( Формула) ).
% Правила трансформаций для пропозициональных формул
тр( ~( ~Х), X) :- !. % Двойное отрицание
тр( X => Y, ~Х v Y) :- !. % Устранение импликации
тр( ~( X & Y), ~Х v ~Y) :- !. % Закон де Моргана
тр( ~( X v Y), ~Х & ~Y) :- !. % Закон де Моргана
тр( X & Y v Z, (X v Z) & (Y v Z) ) :- !.
% Распределительный закон
тр( X v Y & Z, (X v Y) & (X v Z) ) :- !.
% Распределительный закон
тр( X v Y, X1 v Y) :- % Трансформация подвыражения
тр( X, X1), !.
тр( X v Y, X v Y1) :- % Трансформация подвыражения
тр( Y, Y1), !.
тр( ~Х, ~Х1) :- % Трансформация подвыражения
тр( X, X1).
line(); Рис. 16. 8. Преобразование пропозициональных формул в множество
дизъюнктов с записью их в базу данных при помощи assert.
?- транс( ~(( а=>b) & ( b=>c) => ( а=>с)) ), пуск.
Ответ программы "Обнаружено противоречие" будет означать, что исходная формула является теоремой.
Назад | Содержание | Вперёд
Простой интерпретатор программ, управляемых образцами
Для описания модулей, управляемых образцами, мы применим следующую синтаксическую конструкцию:
ЧастьУсловия ---> ЧастьДействия
Часть условия представляет собой список условий:
[ Условие1, Условие2, Условие3, . . .]
где Условие1, Условие2 и т.д. - обычные прологовские цели. Предварительное условие запуска модуля считается выполненным, если все цели, содержащиеся в списке, достигнуты. Часть действия - это список действий:
[ Действие1, Действие2, . . .]
Каждое отдельное действие - это, как и раньше, прологовская цель. Для того, чтобы выполнить список действий, нужно выполнить все действия из списка. Другими словами, все соответствующие цели должны быть удовлетворены. Среди допустимых действий будут действия, соответствующие манипулированию базой данных: добавить, удалить или заменить те или иные объекты базы данных.
На рис. 16.4 показано, как выглядит наша программа вычисления наибольшего общего делителя, записанная в соответствии с введенным нами синтаксисом.
line();% Продукционные правила для нахождения наибольшего общего
% делителя (алгоритм Евклида)
:- ор( 300, fx, число).
[ число X, число Y, X > Y ] --->
[ НовХ is X - Y, заменить( число X, число НовХ) ].
[ число X ] ---> [ write( X), стоп ].
% Начальное состояние базы данных
число 25.
число 10.
число 15.
число 30.
Рис. 16. 4. Программа, управляемая образцами, для получения
наибольшего общего делителя множества чисел.
Самый простой способ реализации этого языка - использовать механизмы управления базой данных, встроенные в Пролог.
Добавить объект в базу данных или удалить объект из базы данных можно, применяя встроенные процедуры
assert ( Объект) retract( Объект)
Заменить один объект на другой также просто:
заменить( Объект1, Объект2) :-
retract( Объект1), !,
assert( Объект2).
Здесь задача оператора отсечения - не допустить, чтобы оператор retract удалил из базы данных более чем один объект (при возвратах).
line();
% Простой интерпретатор для программ, управляемых образцами
% Работа с базой данных производится при помощи процедур
% assert и retract
:- ор( 800, xfx, --->).
пуск :-
Условие ---> Действие,
% правило
проверить( Условие),
% Условие выполнено?
выполнить( Действие).
проверить( [ ]).
% Пустое условие
проверить( [Усл | Остальные]) :-
% проверить конъюнкцию
call( Усл),
% условий
проверить( Остальные).
выполнить( [ стоп] ) :- !.
% Прекратить выполнение
выполнить( [ ]) :-
% Пустое действие (цикл завершен)
пуск.
% Перейти к следующему циклу
выполнить [Д | Остальные] ) :-
саll( Д),
выполнить( Остальные).
заменить( А, В) :-
% Заменить в базе данных А на В
retract( A), !,
assert( В).
line();
Рис. 16. 5. Простой интерпретатор для программ, управляемых образцами.
Простой интерпретатор для программ, управляемых образцами, показан на рис. 16.5. Следует признать, что в интерпретаторе допущены значительные упрощения. Так, например, в него заложено чрезвычайно простое и жесткое правило разрешения конфликтов: всегда запускать первый
из потенциально активных модулей (в соответствии с тем порядком, в котором модули записаны в программе). Таким образом, программисту предоставлено единственное средство управления процессом интерпретации - он может указать тот или иной порядок следования модулей. Начальное состояние базы данных задается в виде прологовских предложений, записанных в исходной программе. Запуск программы производится при помощи вопроса
?- пуск.
Назад | Содержание
| Вперёд
Работа с базой данных
Реляционная модель предполагает, что база данных - это описание некоторого множества отношений. Пролог-программу можно рассматривать как именно такую базу данных: описание отношений частично присутствует в ней в явном виде (факты), а частично - в неявном (правила). Более того, встроенные предикаты дают возможность корректировать эту базу данных в процессе выполнения программ. Это делается добавлением к программе (в процессе вычисления) новых предложений или же вычеркиванием из нее уже существующих. Предикаты, используемые для этой цели, таковы: assert (добавить), asserta, assertz и retract (удалить).
Цель
assert( С)
всегда успешна, а в качестве своего побочного эффекта вызывает "констатацию" предложения С, т. е. добавление его к базе данных. Цель
retract( С)
приводит к противоположному эффекту: удаляет предложение, сопоставимое с С. Следующий диалог иллюстрирует их работу:
?- кризис.
no
? - assert( кризис).
yes
?- кризис.
yes
? - retract( кризис).
yes
?- кризис.
no
Предложения, добавленные к программе таким способом, ведут себя точно так же, как и те, что были в "оригинале" программы. Следующий пример показывает, как с помощью assert и retract можно работать в условиях изменяющейся обстановки. Предположим, что у нас есть такая программа о погоде:
хорошая :-
солнечно, not дождь.
необычная :-
солнечно, дождь.
отвратительная :-
дождь, туман.
дождь.
туман.
Ниже приводится пример диалога с этой программой, во время которого база данных постепенно изменяется:
?- хорошая.
no
?- отвратительная.
yes
?- retract( туман).
yes
?- отвратительная.
no
?- assert( солнечно).
yes
?- необычная.
yes
?- retract( дождь).
уes
?- хорошая.
yes
Добавлять и удалять можно предложения любой формы. Следующий пример показывает, что, кроме того, retract может работать недетерминировано: используя механизм возвратов с помощью только одной цели retract можно удалить целое множество предложений. Предположим, что в программе, с которой мы "консультируемся", есть такие факты:
быстр( энн).
медл( том).
медл( пат).
К этой программе можно добавить правило:
?- assert(
( быстрее( X, Y) :-
быстр( X), медл( Y) ) ).
yes
?- быстрее( А, В).
А = энн
В = том
?- retract( медл( X) ).
Х = том;
X = пат;
nо
?- быстрее( энн, _ ).
nо
Заметьте, что при добавлении нового правила синтаксис требует, чтобы оно (как аргумент assert) было заключено в скобки.
При добавлении нового предложения может возникнуть желание указать, на какое место в базе данных его следует поместить. Такую возможность обеспечивают предикаты asserta и assertz. Цель
asserta( С)
помещает С в начале базы данных. Цель
assertz( С)
- в конце. Вот пример, иллюстрирующий работу этих предикатов:
?- assеrt( р( a)), assertz( р( b) ), asserta( p( c) ).
yes
?- p( X).
Х = с;
Х = а;
Х = b
Между consult и assertz существует связь. Обращение к файлу при помощи consult можно в терминах assertz определить так: считать все термы (предложения) файла и добавить их в конец базы данных.
Одним из полезных применений предиката asserta является накопление уже вычисленных ответов на вопросы.
Пусть, например, в программе определен предикат
решить( Задача, Решение)
Мы можем теперь задать вопрос и потребовать, чтобы ответ на него был запомнен, с тем чтобы облегчить получение ответов на будущие вопросы:
?- решить( задача1, решение),
asserta( решить( Задача1, Решение) ).
Если в первой из приведенных целей будет успех, ответ ( Решение) будет сохранен, а затем использован так же, как и любое другое предложение, при ответе на дальнейшие вопросы. Преимущество такого "запоминания" состоит в том, что на дальнейшие вопросы, сопоставимые с добавленным фактом, ответ будет получен, как правило, значительно быстрее, чем в первый раз. Ответ будет теперь получен как факт, а не как результат вычислений, требующих, возможно, длительного времени.
Развитие этой идеи состоит в использовании assert для порождения всех решений в виде таблицы фактов. Например, создать таблицу произведений всех чисел от 0 до 9 можно так: породить пару чисел Х и Y, вычислить Z, равное Х * Y, добавить эти три числа в виде строки в таблицу произведений, а затем создать искусственно неуспех. Неуспех вызовет возврат, в результате которого будет найдена новая пара чисел, и в таблицу добавится новая строка и т.д. Эта идея реализована в процедуре
таблица :-
L = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
принадлежит( X, L), % Выбрать первый сомножитель
принадлежит( Y, L), % Выбрать второй сомножитель
Z is X*Y,
assert( произв( X,Y,Z) ),
fail.
Вопрос
?- таблица.
потерпит, конечно, неудачу, однако в качестве своего побочного эффекта приведет к добавлению в базу данных целой таблицы произведений. После этого можно, например, спросить, какие пары дают произведения, равные 8:
?- произв( А, В, 8).
А = 1
В = 8;
А = 2
В = 4;
. . .
Здесь следует сделать одно замечание, относящееся к стилю программирования. Приведенные примеры показали некоторые явно полезные применения assert и retract. Однако использование этих отношений требует особой внимательности. Не рекомендуется применять их слишком часто и без должной осторожности - это плохой стиль программирования. Ведь добавляя и удаляя предложения, мы фактически изменяем программу. Поэтому отношения, выполнявшиеся в некоторой ее точке, могут оказаться неверными в другой. В разные моменты времени ответы на одни и те же вопросы будут различными. Таким образом, большое количество обращений к assert и retract может затемнить смысл программы и станет трудно разобрать, что истинно, а что - нет. В результате поведение программы может стать непонятным, трудно объяснимым, и вряд ли можно будет ей доверять.
Расширение программы-примера с помощью правил
Нашу программу-пример можно легко расширить многими интересными способами. Давайте сперва добавим информацию о том, каков пол людей, участвующих в отношении родитель. Это можно сделать, просто добавив в нее следующие факты:
женщина( пам).
мужчина( том).
мужчина( боб).
женщина( лиз).
женщина( пат).
женщина( энн).
мужчина( джим).
Мы ввели здесь два новых отношения - мужчина и женщина. Эти отношения - унарные (или одноместные). Бинарное отношение, такое как родитель, определяет отношение между двумя объектами; унарные же можно использовать для объявления наличия (отсутствия) простых свойств у объектов. Первое из приведенных выше предложений читается так: Пам - женщина. Можно было бы выразить информацию, представляемую этими двумя унарными отношениями (мужчина и женщина), по-другому - с помощью одного бинарного отношения пол. Тогда новый фрагмент нашей программы выглядел бы так:
пол( пам, женский).
пол( том, мужской).
пол( боб, мужской).
. . .
В качестве дальнейшего расширения нашей программы-примера давайте введем отношение отпрыск, которое обратно отношению родитель. Можно было бы определить отпрыск тем же способом, что и родитель, т.е. представив список простых фактов наличия этого отношения для конкретных пар объектов, таких, что один является отпрыском другого. Например:
отпрыск( лиз, том).
Однако это отношение можно определить значительно элегантнее, использовав тот факт, что оно обратно отношению родитель, которое уже определено. Такой альтернативный способ основывается на следующем логическом утверждении:
Для всех X и Y
Y является отпрыском X, если
X является родителем Y.
Эта формулировка уже близка к формализму, принятому в Прологе. Вот соответствующее прологовское предложение, имеющее тот же смысл:
отпрыск( Y, X) :- родитель( X, Y).
Это предложение можно прочитать еще и так:
Для всех X и Y,
если X - родитель Y, то
Y - отпрыск X.
Такие предложения Пролога, как
отпрыск( Y, X) :- родитель( X, Y).
называются правилами. Есть существенное различие между фактами и правилами. Факт, подобный факту
родитель( том, лиз).
это нечто такое, что всегда, безусловно истинно. Напротив, правила описывают утверждения, которые могут быть истинными, только если выполнено некоторое условие. Поэтому можно сказать, что правила имеют условную часть (правая половина правила) и часть вывода (левая половина правила). Вывод называют также головой предложения, а условную часть - его телом. Например:
отпрыск( Y, X) :- родитель( X, Y).
голова тело
Если условие родитель( X, Y) выполняется (оно истинно), то логическим следствием из него является утверждение отпрыск( Y, X).
На приведенном ниже примере проследим, как в действительности правила используются Прологом. Спросим нашу программу, является ли Лиз отпрыском Тома:
? - отпрыск( лиз, том).
В программе нет фактов об отпрысках, поэтому единственный способ ответить на такой вопрос - это применить правило о них. Правило универсально в том смысле, что оно применимо к любым объектам X и Y, следовательно, его можно применить и к таким конкретным объектам, как лиз и том. Чтобы это сделать, нужно вместо Y подставить в него лиз, а вместо X - том. В этом случае мы будем говорить, что переменные X и Y конкретизируются:
X = том и Y = лиз
После конкретизации мы получаем частный случай нашего общего правила. Вот он:
отпрыск( лиз, том) :- родитель( том, лиз).
Условная часть приняла вид:
родитель( том, лиз)
Теперь пролог-система попытается выяснить, выполняется ли это условие (является ли оно истинным). Для этого исходная цель
отпрыск( лиз, том)
заменяется подцелью
родитель( том, лиз)
Эта (новая) цель достигается тривиально, поскольку такой факт можно найти в нашей программе. Это означает, что утверждение, содержащееся в выводе правила, также истинно, и система ответит на вопрос yes (да).
Добавим теперь в нашу программу-пример еще несколько родственных отношений. Определение отношения мать может быть основано на следующем логическом утверждении:
Для всех X и Y
X является матерью Y, если
X является родителем Y и
Х - женщина.
На Пролог это переводится в виде такого правила:
мать( X, Y) :- родитель( X, Y), женщина( X).
Запятая между двумя условиями указывает ка конъюнкцию условий.
Это означает, что они должны быть выполнены оба одновременно.

Рис. 1. 3. Графы отношений родительродителя, мать и отпрыск,
определенных через другие отношения.
Такие отношения как родитель, отпрыск и мать можно изобразить в виде диаграмм, приведенных на рис. 1.3. Они нарисованы с учетом следующих соглашений. Вершины графа соответствуют объектам, т.е. аргументам отношений. Дуги между вершинами соответствуют бинарным (двуместным) отношениям. Дуги направлены от первого аргумента к второму. Унарные отношения на диаграмме изображаются просто пометкой соответствующих объектов именем отношения. Отношения, определяемые через другие отношения, представлены штриховыми дугами. Таким образом, любую диаграмму следует понимать так: если выполнены отношения, изображенные сплошными дугами, тогда и отношение, изображенное штриховой дугой, тоже выполнено. В соответствии с рис. 1.3, отношение родительродителя можно сразу записать на Прологе:
родительродителя( X, Z) :- родитель( X, Y),
родитель( Y, Z).
Здесь уместно сделать несколько замечаний о внешнем виде нашей программы. Пролог дает почти полную свободу расположения текста на листе. Так что можно вставлять пробелы и переходить к новой строке в любом месте текста по вкусу. Вообще мы хотим сделать так, чтобы наша программа имела красивый и аккуратный вид, а самое главное, легко читалась. Для этого мы часто будем помещать голову предложения и каждую цель на отдельной строке. При этом цели мы будем писать с отступом, чтобы сделать разницу между головой и целями более заметной. Например, правило родительродителя в соответствии с этими соглашениями запишется так:
родительродителя( X, Z) :-
родитель( X, Y),
родитель( Y, Z).
На рис. 1.4 показано отношение сестра:
Для любых X и Y
X является сестрой Y, если
(1) у X и Y есть общий родитель, и
(2) X - женщина.

Рис. 1. 4. Определение отношения сестра.
Граф на рис. 1. 4 можно перевести на Пролог так:
сестра( X, Y) :-
родитель( Z, X),
родитель( Z, Y),
женщина( X).
Обратите внимание на способ, с помощью которого выражается требование "у X и Y есть общий родитель". Была использована следующая логическая формулировка: "некоторый Z должен быть родителем X и этот же самый Z должен быть родителем Y". По-другому, менее красиво, можно было бы сказать так: "Z1 - родитель X, Z2 - родитель Y и Z1 равен Z2".
Теперь можно спросить:
?- сестра( энн, пат).
Как и ожидается, ответ будет "yes" (да) (см. рис. 1.1). Мы могли бы заключить отсюда, что определенное нами отношение сестра работает правильно. Тем не менее в нашей программе есть маленькое упущение, которое обнаружится, если задать вопрос: "Кто является сестрой Пат?"
?- сестра( X, пат).
Система найдет два ответа, один из которых может показаться неожиданным:
X = энн;
X = пат
Получается, что Пат - сестра себе самой?! Наверное, когда мы определяли отношение сестра, мы не имели этого ввиду. Однако ответ Пролога совершенно логичен, поскольку он руководствовался нашим правилом, а это правило ничего не говорит о том, что, если X - сестра Y, то X и Y не должны совпадать. Пролог (с полным правом) считает, что X и Y могут быть одним и тем же объектом и в качестве следствия из этого делает вывод, что любая женщина, имеющая родителя, является сестрой самой себе.
Чтобы исправить наше правило о сестрах, его нужно дополнить утверждением, что X и Y должны различаться. В следующих главах мы увидим, как это можно сделать, в данный же момент мы предположим, что отношение различны уже известно пролог-системе и что цель
различны( X, Y)
достигается тогда и только тогда, когда X и Y не равны. Усовершенствованное правило для отношения сестра примет тогда следующий вид:
сестра( X, Y) :-
родитель( Z, X),
родители( Z, Y),
женщина( X),
различны( X, Y).
Некоторые важные моменты этого раздела: Пролог-программы можно расширять, добавляя в них новые предложения. Прологовские предложения бывают трех типов: факты, правила и вопросы. Факты содержат утверждения, которые являются всегда, безусловно верными. Правила содержат утверждения, истинность которых зависит от некоторых условий. С помощью вопросов пользователь может спрашивать систему о том, какие утверждения являются истинными. Предложения Пролога состоят из головы и тела. Тело - это список целей, разделенных запятыми. Запятая понимается как конъюнкция. Факты - это предложения, имеющие пустое тело.
Вопросы имеют только тело. Правила имеют голову и (непустое) тело. По ходу вычислений вместо переменной может быть подставлен другой объект. Мы говорим в этом случае, что переменная конкретизирована. Предполагается, что на переменные действует квантор всеобщности, читаемый как "для всех...". Однако для переменных, появляющихся только в теле, возможны и другие формулировки. Например,
имеетребенка( X) :- родитель( X, Y).
можно прочитать двумя способами:
(а) Для всех X и Y,
если X - отец Y, то
X имеет ребенка.
(б) Для всех X,
X имеет ребенка, если
существует некоторый Y, такой, что
X - родитель Y.
Различные виды равенства
В каких случаях мы считаем, что два терма равны? До сих пор мы рассматривали три вида равенства в Прологе. Первый был связан с сопоставлением и записывался так:
Х = Y
Это равенство верно, если Х и Y сопоставимы. Следующий вид равенства записывался в виде
Х is E
Такое равенство выполняется, если Х сопоставим со значением арифметического выражения E. Мы также рассматривали равенства вида
Е1 =:= Е2
которые верны, если равны значения арифметических выражений Е1 и Е2. Наоборот, если значения двух арифметических выражений не равны, мы пишем
Е1 =/= Е2
Иногда нам может понадобиться более строгий вид равенства - буквальное равенство двух термов. Этот вид реализован еще одним встроенным предикатом, записываемым как инфиксный оператор '==':
Т1 == Т2
Это равенство выполняется, если термы Т1 и Т2 идентичны, т. е. имеют в точности одинаковую структуру, причем все соответствующие компоненты совпадают. В частности, должны совпадать и имена переменных. Отношение "не идентичны", дополнительное к данному, записывается так:
Tl \== T2
Приведем несколько примеров:
?- f( a, b) == f( а, b).
yes
?- f( a, b) == f( a, X).
nо
?- f( a, X) == f( a, Y).
no
?- X \== Y.
yes
?- t( X, f( a, Y) ) == t( X, f( a, Y) ).
yes
Давайте в качестве примера переопределим отношение
счетчик( Терм, Список, N)
из разд. 7.1. Пусть на этот раз N будет числом буквальных вхождений Терм'а в Список:
счетчик( _, [ ], 0).
счетчик( Терм, [Голова | L], N) :-
Терм == Голова, !,
счетчик( Терм, L, N1),
N is N1 + 1;
счетчик( Терм, L, N).
Назад | Содержание | Вперёд
Разработка оболочки
Если мы посмотрим на правила наших двух маленьких баз знаний рис. 14.5 и 14.7, мы сразу увидим, что они по своему смыслу эквивалентны правилам Пролога. Однако, с точки зрения синтаксиса Пролога, эти правила в том виде, как они написаны, соответствуют всего лишь фактам. Для того, чтобы заставить их работать, самое простое, что может прийти в голову, это переписать их в виде настоящих прологовских правил. Например:
Животное это млекопитающее :-
Животное имеет шерсть;
Животное 'кормит детенышей' молоком.
Животное это хищник :-
Животное это млекопитающее,
Животное ест мясо.
. . .
Теперь эта программа сможет подтвердить, что тигр по имени Питер - это действительно тигр, если мы добавим в нее некоторые из свойств Питера (в виде прологовских фактов):
питер имеет шерсть.
питер ленив.
питер большой.
питер имеет 'рыжевато-коричневый цвет'.
питер имеет 'черные полосы'.
питер ест мясо.
Тогда мы можем спросить:
?- питер это тигр.
yes
?- питер это гепард.
no
Хотя пролог-система и отвечает на вопросы, используя для этого нашу базу знаний, нельзя сказать, что ее поведение вполне соответствует поведению эксперта.
Это происходит по крайней мере по двум причинам:
(1) Мы не можем попросить систему объяснить свой ответ; например, как
она установила, что Питер это тигр, и почему
Питер это не гепард.
(2) Прежде, чем задать вопрос, нужно ввести в систему всю необходимую информацию (в виде прологовских фактов). Но тогда пользователь, возможно, введет какую-нибудь лишнюю информацию (как в нашем примере) или же упустит какую-нибудь информацию, имеющую решающее значение. В первом случае будет проделана ненужная работа, а во втором - система будет давать неверные ответы.
Для того, чтобы исправить эти два недостатка, мы нуждаемся в более совершенном способе взаимодействия между пользователем и системой во время и после завершения процесса рассуждений. Поставим себе целью добиться того, чтобы система взаимодействовала с пользователем так, как в следующем примере диалога (ответы пользователя даются полужирным шрифтом, реплики пролог-системы - курсивом):
Пожалуйста, спрашивайте:
питер это тигр.
Это правда: питер имеет шерсть?
да.
Это правда: питер ест мясо?
нет.
Это правда: питер имеет острые зубы?
да.
Это правда: питер имеет когти?
почему.
Чтобы проверить по прав3, что питер это хищник,
Чтобы проверить по прав5, что питер это тигр
Это был ваш вопрос
Это правда: питер имеет когти?
да.
Это правда: питер имеет глаза, направленные вперед?
да.
Это правда: питер имеет рыжевато-коричневый цвет?
да.
Это правда: питер имеет черные полосы?
да.
(питер это тигр) это правда
Хотите узнать, как?
да.
питер это тигр
было выведено по прав5 из
питер это хищник,
было выведено по прав3 из
питер это млекопитающее
было выведено по прав1 из
питер имеет шерсть
было сказано
и
питер имеет острые зубы
было сказано
и
питер имеет когти
было сказано
и
питер имеет глаза, направленные вперед
было сказано
и
питер имеет рыжевато-коричневый цвет
было сказано
и
питер имеет черные полосы
было сказано
Как видно из диалога, система задает пользователю вопросы, касающиеся "примитивной" информации, например:
Это правда: питер ест мясо?
Эту информацию нельзя отыскать в базе знаний или вывести из другой информации. На подобные вопросы пользователь может отвечать двумя способами:
(1) сообщив системе в качестве ответа на вопрос необходимую информацию или
(2) спросив систему, почему
эта информация необходима.
Последняя из двух возможностей полезна, поскольку она позволяет пользователю заглянуть внутрь системы и увидеть ее текущие намерения. Пользователь спросит "почему" в том случае, когда вопрос системы покажется ему не относящимся к делу либо когда ответ на вопрос системы потребует от него дополнительных усилий. Из объяснений системы пользователь поймет, стоит ли информация, которую запрашивает система, тех дополнительных усилий, которые необходимо приложить для ее приобретения.Предположим, например, что система спрашивает: "Это животное ест мясо?" Пользователь, не знающий ответа на этот вопрос, поскольку он никогда не видел, как это животное ело что-либо, может решить, что не стоит ждать, пока он застанет животное за едой и убедится, что оно действительно ест мясо.
Для того, чтобы заглянуть внутрь системы и до какой-то степени представить себе протекающий в ней процесс рассуждений, можно воспользоваться прологовскими средствами трассировки. Но эти средства в большинстве случаев окажутся недостаточно гибкими для наших целей. Поэтому, вместо того, чтобы воспользоваться собственным механизмом интерпретации Пролога, который не сможет справиться с нужным нам способом взаимодействия с пользователем, мы создадим свое средство интерпретации в виде специальной надстройки над пролог-системой. Этот новый интерпретатор будет включать в себя средства для взаимодействия с пользователем.
Reаd и write
Встроенный предикат read используется для чтения термов из текущего входного потока. Цель
read( X)
вызывает чтение следующего терма Т и сопоставление его с X. Если Х - переменная, то в результате Х конкретизируется и становится равным Т. Если сопоставление терпит неудачу, цель read( X) тоже терпит неудачу. Предикат read - детерминированный в том смысле, что в случае неуспеха не происходит возврата для ввода следующего терма. После каждого терма во входном файле должна стоять точка или пробел, или символ возврата каретки.
Если read( X) вычисляется в тот момент, когда достигнут конец текущего входного файла, тогда Х конкретизируется атомом end_of_file (конец файла).
Встроенный предикат write выводит терм. Поэтому цель
write( X)
выведет терм Х в текущий выходной файл. Х будет выведен в той же стандартной форме, в какой обычно пролог-система изображает на экране или распечатке значения переменных. Полезной особенностью Пролога является то, что процедура write "знает", как изображать любой терм, как бы сложен он не был.
Существуют дополнительные встроенные предикаты для форматирования вывода. Они вставляют пробелы в дополнительные строки в выходной поток. Цель
tab( N)
выводит N пробелов. Предикат nl (без аргументов) приводит к переходу на новую строку.
Следующие примеры иллюстрируют использование этих процедур.
Предположим, у нас есть процедура для вычисления кубов чисел:
куб( N, С) :-
С is N * N * N.
Предположим далее, что мы хотим применить ее для вычисления кубов элементов некоторой последовательности чисел. Это можно сделать с помощью последовательности вопросов:
?- куб( 2, X).
Х = 8
?- ку6( 5, Y).
Y = 125
?- куб( 12, Z).
Z = 1728
Для получения каждого результата нам придется набирать соответствующую цель. Давайте теперь изменим эту программу так, чтобы процедура куб
сама читала соответствующие данные. Теперь программа будет сама читать данные и выводить их кубы до тех пор, пока не будет прочитан атом стоп:
куб :-
read( X),
обработать( X).
обработать( стоп) :- !.
обработать( N) :-
С is N * N * N,
write( С),
куб.
Это был пример программы, декларативный смысл которой трудно сформулировать. В то же время ее процедурный смысл совершенно ясен: чтобы вычислить куб, сначала нужно считать X, а затем его обработать; если Х = стоп, то все сделано, иначе вывести Х3 и рекурсивно запустить процедуру куб для обработки остальных чисел.
С помощью этой новой процедуры таблица кубов чисел может быть получена таким образом:
?- куб.
2.
8
5.
125
12.
1728
стоп.
yes
Числа 2, 5 и 12 были введены пользователем с терминала, остальные числа были выведены программой.
Заметьте, что после каждого числа, введенного пользователем, должна стоять точка, которая сигнализирует о конце терма.
Может показаться, что приведённую процедуру куб
можно упростить. Однако следующая попытка такого упрощения является ошибочной:
куб :-
read( стоп), !.
куб :-
read( N),
С is N * N * N,
write( С),
куб.
Причина, по которой эта процедура работает неправильно, станет очевидной, если проследить, какие действия она выполняет с входным аргументом, скажем с числом 5. Цель read( стоп)
потерпит неудачу при чтении этого числа, и оно будет потеряно навсегда. Следующая цель read
введет следующий терм. С другой стороны может случиться, что сигнал стоп будет считан целью read( N), что приведет к попытке перемножить нечисловую информацию.
Процедура куб ведет диалог между пользователем и программой. В таких случаях обычно желательно, чтобы программа перед тем, как читать с терминала новые данные, дала сигнал пользователю о том, что она готова к приему информации, а также, возможно, и о том, какого вида информация ожидается. Это делается обычно путем выдачи "приглашения" перед чтением. Нашу процедуру куб можно для этого изменить, например, так:
куб :-
write( 'Следующее число, пожалуйста:'),
read( X),
обработать( X).
о6работать( стоп) :- !.
обработать( N) :-
С is N * N * N,
write( 'Куб'), write( N), write( 'равен').
write( С), nl,
куб.
Разговор с новой версией мог бы быть, например, таким:
?- куб.
Следующее число, пожалуйста: 5.
Куб 5 равен 125
Следующее число, пожалуйста: 12.
Куб 12 равен 1728
Следующее число, пожалуйста: стоп.
yes
В некоторых реализациях для того, чтобы приглашение появилось на экране перед чтением, необходимо выдать дополнительный запрос (такой, скажем, как ttyflush) после записи.
В последующих разделах мы увидим некоторые типичные примеры операций, в которых участвуют чтение и запись.
Реализация
Теперь мы приступим к реализации нашей оболочки, следуя тем идеям, которые обсуждались в предыдущем разделе. На рис. 14.9 показаны основные объекты, которыми манипулирует оболочка. Цель - это вопрос, подлежащий рассмотрению; Трасса - это цепочка, составленная из "целей-предков" и правил, находящихся между вершиной Цель и вопросом самого верхнего уровня; Ответ - решающее дерево типа И / ИЛИ для вершины Цель.

Рис. 14. 9. Отношение рассмотреть( Цель, Трасса, Ответ).
Ответ - это И / ИЛИ решающее дерево для целевого утверждения Цель.
Основными процедурами оболочки будут:
рассмотреть( Цель, Трасса, Ответ)
Эта процедура находит ответ Ответ на вопрос Цель. Процедура
ответпольз( Цель, Трасса, Ответ)
порождает решения для тех вопросов Цель, которые можно задавать пользователю. Она спрашивает пользователя об истинности утверждения Цель, а также отвечает на вопросы "почему". Процедура
выдать( Ответ)
выводит результат и отвечает на вопросы "как". Все эти процедуры приводятся в действие процедурой-драйвером эксперт.
Рекурсивное определение правил
Давайте добавим к нашей программе о родственных связях еще одно отношение - предок. Определим его через отношение родитель. Все отношение можно выразить с помощью двух правил. Первое правило будет определять непосредственных (ближайших) предков, а второе - отдаленных. Будем говорить, что некоторый является отдаленным предком некоторого Z, если между X и Z существует цепочка людей, связанных

Рис. 1. 5. Пример отношения предок:
(а) X - ближайший предок Z; (b) X - отдаленный предок Z.
между собой отношением родитель-ребенок, как показано на рис.1.5. В нашем примере на рис. 1.1 Том - ближайший предок Лиз и отдаленный предок Пат.
Первое правило простое и его можно сформулировать так:
Для всех X и Z,
X - предок Z, если
X - родитель Z.
Это непосредственно переводится на Пролог как
предок( X, Z) :-
родитель( X, Z).
Второе правило сложнее, поскольку построение цепочки отношений родитель может вызвать некоторые трудности. Один из способов определения отдаленных родственников мог бы быть таким, как показано на рис. 1.6. В соответствии с ним отношение предок определялось бы следующим множеством предложений:
предок( X, Z) :-
родитель( X, Z).
предок( X, Z) :-
родитель( X, Y),
родитель( Y, Z).
предок( X, Z) :-
родитель( X, Y1),
родитель( Yl, Y2),
родитель( Y2, Z).
предок( X, Z) :-
родитель( X, Y1),
родитель( Y1, Y2),
родитель( Y2, Y3),
родитель( Y3, Z).
. . .

Рис. 1. 6. Пары предок-потомок, разделенных разным числом поколений.
Эта программа длинна и, что более важно, работает только в определенных пределах. Она будет обнаруживать предков лишь до определенной глубины фамильного дерева, поскольку длина цепочки людей между предком и потомком ограничена длиной наших предложений в определении отношения.
Существует, однако, корректная и элегантная формулировка отношения предок - корректная в том смысле, что будет работать для предков произвольной отдаленности. Ключевая идея здесь - определить отношение предок через него самого. Рис 1.7 иллюстрирует эту идею:
Для всех X и Z,
X - предок Z, если
существует Y, такой, что
(1) X - родитель Y и
(2) Y - предок Z.
Предложение Пролога, имеющее тот же смысл, записывается так:
предок( X, Z) :-
родитель( X, Y),
предок( Y, Z).
Теперь мы построили полную программу для отношения предок, содержащую два правила: одно для ближайших предков и другое для отдаленных предков. Здесь приводятся они оба вместе:
предок( X, Z) :-
родитель( X, Z).
предок( X, Z) :-
родитель( X, Y),
предок( Y, Z).

Рис 1. 7. Рекурсивная формулировка отношения предок.
Ключевым моментом в данной формулировке было использование самого отношения предок в его определении. Такое определение может озадачить - допустимо ли при определении какого-либо понятия использовать его же, ведь оно определено еще не полностью. Такие определения называются рекурсивными. Логически они совершенно корректны и понятны; интуитивно это ясно, если посмотреть на рис. 1.7. Но будет ли в состоянии пролог-система использовать рекурсивные правила? Оказывается, что пролог-система очень легко может обрабатывать рекурсивные определения. На самом деле, рекурсия - один из фундаментальных приемов программирования на Прологе. Без рекурсии с его помощью невозможно решать задачи сколько-нибудь ощутимой сложности.
Возвращаясь к нашей программе, можно теперь задать системе вопрос: "Кто потомки Пам?" То есть: "Кто тот человек, чьим предком является Пам ?"
?- предок( пам, X).
X = боб;
X = энн;
X = пат;
X = джим
Ответы системы, конечно, правильны, и они логически вытекают из наших определений отношений предок и родитель. Возникает, однако, довольно важный вопрос: "Как в действительности система использует программу для отыскания этих ответов?"
Неформальное объяснение того, как система это делает, приведено в следующем разделе. Но сначала давайте объединим все фрагменты нашей программы о родственных отношениях, которая постепенно расширялась по мере того, как мы вводили в нее новые факты и правила. Окончательный вид программы показан на рис. 1.8.
При рассмотрении рис. 1.8 следует учесть два новых момента: первый касается понятия "процедура", второй - комментариев в программах. Программа, приведенная на рис. 1.8, определяет несколько отношений - родитель, мужчина, женщина, предок и т.д. Отношение предок, например, определено с помощью двух предложений. Будем говорить, что эти два предложения входят в состав отношения
line(); родитель( пам, боб). % Пам - родитель Боба
родитель( том, боб).
родитель( том, лиз).
родитель( бoб, энн).
родитель( боб, пат).
родитель( пат, джим).
женщина( пам). % Пам - женщина
мужчина( том). % Том - мужчина
мужчина( боб).
женщина( лиз).
женщина( энн).
женщина( пат).
мужчина( джим).
отпрыск( Y, X) :- % Y - отпрыск X, если
родитель( X, Y). % X - родитель Y
мать( X, Y) :- % X - мать Y, если
родитель( X, Y), % X - родитель Y и
женщина( X). % X - женщина
родительродителя( X, Z) :-
% X - родитель родителя Z, если
родитель( X, Y), % X - родитель Y и
родитель( Y, Z). % Y - родитель Z
сестра( X, Y) :- % X - сестра Y
родитель( Z, X),
родитель( Z, Y)
% X и Y имеют общего родителя
женщина( X, Y), % X - женщина и
различны( X, Y). % X отличается от Y
предок( X, Z) :- % Правило пр1: X - предок Z
родитель( X, Z).
предок( X, Z) :- % Правило пр2: X - предок Z
родитель( X, Y),
предок( Y, Z).
line(); Рис. 1. 8. Программа о родственных отношениях.
предок. Иногда бывает удобно рассматривать в целом все множество предложений, входящих в состав одного отношения. Такое множество называется процедурой.
На рис. 1.8 два предложения, входящие в состав отношения предок, выделены именами "пр1" и "пр2", добавленными в программу в виде комментариев. Эти имена будут использоваться в дальнейшем для ссылок на соответствующие правила. Вообще говоря, комментарии пролог-системой игнорируются. Они нужны лишь человеку, который читает программу. В Прологе комментарии отделяются от остального текста программы специальными скобками "/*" и "*/". Таким образом, прологовский комментарий выглядит так
/* Это комментарий */
Другой способ, более практичный для коротких комментариев, использует символ процента %. Все, что находится между % и концом строки, расценивается как комментарии:
% Это тоже комментарий
Решение числового ребуса с использованием nonvar
Известным примером числового ребуса является
| + | D O N A L D |
| G E R A L D | |
| R O B E R T |
Задача состоит в том. чтобы заменить буквы D, О, N и т.д. на цифры таким образом, чтобы вышеприведенная сумма была правильной. Разным буквам должны соответствовать разные цифры, иначе возможно тривиальное решение, например, все буквы можно заменить на нули.
Определим отношение
сумма( Nl, N2, N)
где Nl, N2 и N представляют три числа данного ребуса. Цель cyммa(Nl, N2, N) достигается, если существует такая замена букв цифрами, что N1+N2 = N.
Первым шагом к решению будет выбор представления чисел Nl, N2 и N в программе. Один из способов - представить каждое число в виде списка его цифр. Например, число 255 будет тогда представляться списком [2, 2, 5]. Поскольку значения цифр нам не известны заранее, каждая цифра будет обозначаться соответствующей неинициализированной переменной. Используя это представление, мы можем сформулировать задачу так:
[ D, O, N, A, L, D ]
+ [ G, E, R, A, L, D ]
= [ R, О, B, E, R, T ]
Теперь задача состоит в том. чтобы найти такую конкретизацию переменных D, О, N и т.д., для которой сумма верна. После того, как отношение сумма будет запрограммировано, задание для пролог-системы на решение ребуса будет иметь вид
?- сумма( [D, O, N, A, L, D], [G, E, R, A, L, D],
[R, O, В, Е, R, T ).
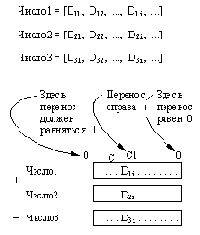
Рис. 7. 1. Поразрядное сложение. Отношения в показанном i-м
разряде такие: D3i = (C1 + D1i
+ D2i) mod 10; C = (C1 + D1i + D2i)
div 10 (div - целочисленное деление, mod - остаток от деления).
Для определения отношения сумма над списками цифр нам нужно запрограммировать реальные правила суммирования в десятичной системе счисления. Суммирование производится цифра за цифрой, начиная с младших цифр в сторону старших, всякий раз учитывая цифру переноса справа. Необходимо также сохранять множество допустимых цифр, т.е. цифр, которые еще не были использованы для конкретизации уже встретившихся переменных. Поэтому, вообще говоря, кроме трех чисел Nl, N2 и N в рассмотрении должна участвовать некоторая дополнительная информация, как показано на рис. 7.1: перенос перед сложением перенос после сложения множество цифр, доступных перед сложением оставшиеся цифры, не использованные при сложении Для формулировки отношения сумма мы снова воспользуемся принципом обобщения задачи: введем вспомогательное, более общее отношение сумма1. Это отношение будет иметь несколько дополнительных аргументов, соответствующих той дополнительной информации, о которой говорилось выше:
сумма1( Nl, N2, N, C1, С, Цифры1, Цифры)
Здесь Nl, N2 и N - наши три числа, как и в отношении сумма, С1 - перенос справа (до сложения Nl и N2), а С - перенос влево (после сложения). Пример:
?- сумма1( [H, E], [6, E], [U, S], l, l,
[1, 3, 4, 7, 8, 9], Цифры ).
Н = 8
Е = 3
S = 7
U = 4
Цифры = [1, 9]
Если Nl и N удовлетворяют отношению сумма, то, как показано на рис. 7.1, С1 и С должны быть равны 0. Цифры1 - список цифр, которые не были использованы для конкретизации переменных. Поскольку мы допускаем использование в отношении сумма любых цифр, ее определение в терминах отношения сумма1 выглядит так:
сумма( Nl, N2, N) :-
cyммa1( Nl, N2, N, 0, 0, [0, l, 2, 3, 4, 5, 6, 7, 8, 9], _ ).
Бремя решения задачи переложено теперь на отношение сумма1. Но это отношение является уже достаточно общим, чтобы можно было определить его рекурсивно. Без ограничения общности мы предположим, что все три списка, представляющие три числа, имеют одинаковую длину. Наш пример, конечно, удовлетворяет этому условию, но если это не так, то всегда можно приписать слева нужное количество нулей к более "короткому" числу.
Определение отношения сумма1 можно разбить на два случая:
(1) Все три числа представляются пустыми списками. Тогда
сумма1( [ ], [ ], [ ], 0, 0, Циф, Циф).
(2) Все три числа имеют какую-то самую левую цифру и справа от нее - остальные цифры. То есть, они имеют вид:
[D1 | Nl], [D2 | N2], [D | N]
В этом случае должны выполняться два условия:
(а) Оставшиеся цифры, рассматриваемые как три числа Nl, N2 и N, сами должны удовлетворять отношению сумма1, выдавая влево некоторый перенос С2 и оставляя некоторое подмножество неиспользованных цифр Циф2.
(b) Крайние левые цифры D1, D2 и D, а также перенос С2 должны удовлетворять отношению, показанному на рис. 7.1: С2, D1 и D2 складываются, давая в результате D и перенос влево. Это условие в нашей программе формулируется в виде отношения суммацифр.
Переводя это на Пролог, получаем:
сумма1( [D1 | N1], [D2 | N2], [D | N], С1, С, Циф1, Циф) :-
сумма1( Nl, N2, N, С1, С2, Циф1, Циф2),
суммацифр( D1, D2, С2, D, С, Циф2, Циф).
Осталось только описать на Прологе отношение суммацифр. В его определении есть одна тонкая деталь, касающаяся применения металогического предиката nonvar. D1, D2 и D должны быть десятичными цифрами. Если хоть одна из этих переменных еще не конкретизирована, ее нужно конкретизировать какой-нибудь цифрой из списка Циф2. Как только такая конкретизация произошла, эту цифру нужно удалить из множества доступных цифр. Если D1, D2 и D уже конкретизированы, тогда, конечно, ни одна из доступных цифр "потрачена" не будет. В программе эти действия реализуются при помощи недетерминированного вычеркивания элемента списка. Если этот элемент - не переменная, ничего не вычеркивается (конкретизации не было). Вот эта программа:
удалить( Элемент, Список, Список) :-
nonvar( Элемент), !.
удалить( Элемент, [Элемент | Список ], Список).
удалить(Элемент, [А | Список], [А | Список1]) :-
удалить( Элемент, Список, Список1).
Полная программа для решения арифметических ребусов приводится на рис. 7.2. В программу включены также определения двух ребусов. Вопрос к пролог-системе для ребуса про DONALD'a, GERALD'a и ROBERT'a с использованием этой программы выглядит так:
?- ребус1( N1, N2, N), сумма( N1, N2, N).
line(); % Решение числовых ребусов
сумма( N1, N2, N) :-
% Числа представлены в виде списков цифр
сумма1( N1, N2, N,
0, 0,
% Перенос справа и перенос влево равны 0
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9], _ ).
% Все цифры доступны
сумма1( [ ], [ ], [ ], 0, 0, Цифры, Цифры).
сумма1( [D1 | N1], [D2 | N2], [D | N], C1, С, Циф1, Циф) :-
сумма1( Nl, N2, N, C1, C2, Циф1, Циф2),
суммацифр( Dl, D2, C2, С, Циф2, Циф).
суммацифр( Dl, D2, C1, D, С, Циф1, Циф) :-
удалить( D1, Циф1, Циф2),
% Выбор доступной цифры для D1
удалить( D2, Циф2, Циф3),
% Выбор доступной цифры для D2
удалить( D, Циф3, Циф),
% Выбор доступной цифры для D
S is D1 + D2 + C1,
D is S mod 10,
С is S div 10.
удалить( A, L, L) :-
nonvar( A), !.
% Переменная А уже конкретизирована
удалить( А, [А | L], L).
удалить( А, [В | L], [В | L1]) :-
удалить( A, L, L1).
% Примеры ребусов
ребус1( [D, O, N, A, L, D],
[G, E, R, A, L, D],
[R, O, B, E, R, T].
ребус2( [0, S, E, N, D],
[0, M, O, R, E],
[M, O, N, E, Y].
line(); Рис. 7. 2. Программа для арифметических ребусов.
Иногда этот ребус упрощают, сообщая часть решения в виде дополнительного ограничения, например D равно 5. В такой форме ребус можно передать пролог-системе при помощи сумма1:
? - сумма1( [5, O, N, A, L, 5],
[G, E, R, A, L, 5],
[R, O, B, E, R, T],
0, 0, [0, 1, 2, 3, 4, 6, 7, 8, 9], _ ).
Интересно, что в обоих случаях существует только одно решение, т.е. только один способ заменить буквы цифрами.
в постановке вопросов, касающихся этих
Программирование на Прологе состоит в определении отношений и в постановке вопросов, касающихся этих отношений. Программа состоит из предложений. Предложения бывают трех типов: факты, правила и вопросы. Отношение может определяться фактами, перечисляющими n-ки объектов, для которых это отношение выполняется, или же оно может определяться правилами. Процедура - это множество предложений об одном и том же отношении. Вопросы напоминают запросы к некоторой базе данных. Ответ системы на вопрос представляет собой множество объектов, которые удовлетворяют запросу. Процесс, в результате которого пролог-система устанавливает, удовлетворяет ли объект запросу, часто довольно сложен и включает в себя логический вывод, исследование различных вариантов и, возможно, возвраты. Все это делается автоматически самой пролог-системой и по большей части скрыто от пользователя. Различают два типа смысла пролог-программ: декларативный и процедурный. Декларативный подход предпочтительнее с точки зрения программирования. Тем не менее, программист должен часто учитывать также и процедурные детали. В данной главе были введены следующие понятия:
предложение, факт, правило, вопрос
голова предложения, тело предложения
рекурсивное правило
рекурсивное определение
процедура
атом, переменная
конкретизация переменной
цель
цель достижима, цель успешна
цель недостижима,
цель имеет неуспех, цель терпит неудачу
возврат
декларативный смысл, процедурный смысл.
Сбалансированные или приближенно сбалансированные деревья
2-3 деревья и AVL-деревья, представленные в настоящей главе, - это примеры сбалансированных деревьев. Сбалансированные или приближенно сбалансированные деревья гарантируют эффективное выполнение трех основных операций над деревьями: поиск, добавление и удаление элемента. Время выполнения этих операций пропорционально log n, где n - число вершин дерева.
Пространство состояний есть формализм для
Пространство состояний есть формализм для представления задач. Пространство состояний - это направленный граф, вершины которого соответствуют проблемным ситуациям, а дуги - возможным ходам. Конкретная задача определяется стартовой вершиной и целевым условием. Решению задачи соответствует путь в графе. Таким образом, решение задачи сводится к поиску пути в графе. Оптимизационные задачи моделируются приписыванием каждой дуге пространства состояний некоторой стоимости. Имеются две основных стратегии поиска в пространстве состояний - поиск в глубину и поиск в ширину. Поиск в глубину программируется наиболее легко, однако подвержен зацикливаниям. Существуют два простых метода предотвращения зацикливания: ограничить глубину поиска и не допускать дублирования вершин. Реализация поиска в ширину более сложна, поскольку требуется сохранять множество кандидатов. Это множество может быть с легкостью представлено списком списков, но более экономное представление - в виде дерева. Поиск в ширину всегда первым обнаруживает самое короткое решение, что не верно в отношении стратегии поиска в глубину. В случае обширных пространств состояний существует опасность комбинаторного взрыва. Обе стратегии плохо приспособлены для борьбы с этой трудностью. В таких случаях необходимо руководствоваться эвристиками. В этой главе были введены следующие понятия:
пространство состояний
стартовая вершина, целевое условие,
решающий путь
стратегия поиска
поиск в глубину, поиск в ширину
эвристический поиск.
Для оценки степени удаленности некоторой
Для оценки степени удаленности некоторой вершины пространства состояний от ближайшей целевой вершины можно использовать эвристическую информацию. В этой главе были рассмотрены численные эвристические оценки. Эвристический принцип поиска с предпочтением направляет процесс поиска таким образом, что для продолжения поиска всегда выбирается вершина, наиболее перспективная с точки зрения эвристической оценки. В этой главе был запрограммирован алгоритм поиска, основанный на указанном принципе и известный в литературе как А*-алгоритм. Для того, чтобы решить конкретную задачу при помощи А*-алгоритма, необходимо определить пространство состояний и эвристическую функцию. Для сложных задач наиболее трудным моментом является подбор хорошей эвристической функции. Теорема о допустимости помогает установить, всегда ли А*-алгоритм, использующий некоторую конкретную эвристическую функцию, находит оптимальное решение.
это формальный аппарат для представления
И / ИЛИ-граф - это формальный аппарат для представления задач. Такое представление является наиболее естественным и удобным для задач, которые разбиваются на независимые подзадачи. Примером могут служить игры. Вершины И / ИЛИ-графа бывают двух типов: И- вершины и ИЛИ-вершины. Конкретная задача определяется стартовой вершиной и целевым условием. Решение задачи представляется решающим деревом. Для моделирования оптимизационных задач в И / ИЛИ-граф можно ввести стоимости дуг и вершин. Процесс решения задачи, представленной И / ИЛИ-графом, включает в себя поиск в графе. Стратегия поиска в глубину предусматривает систематический просмотр графа и легко программируется. Однако эта стратегия может привести к неэффективности из-за комбинаторного взрыва. Для оценки трудности задач можно применить эвристики, а для управления поиском - принцип эвристического поиска с предпочтением. Эта стратегия более трудна в реализации. В данной главе были разработаны прологовские программы для поиска в глубину и поиска с предпочтением в И / ИЛИ-графах. Были введены следующие понятия:
И / ИЛИ-графы
И-дуги, ИЛИ-дуги
И-вершины, ИЛИ-вершины
решающий путь, решающее дерево
стоимость дуг и вершин
эвристические оценки в И / ИЛИ-графах
"возвращенные" оценки
поиск в глубину в И / ИЛИ-графах
поиск с предпочтением в И / ИЛИ-графах
Обычно от экспертных систем требуют
Обычно от экспертных систем требуют выполнения следующих функций:
решение задач в заданной предметной области,
объяснение процесса решения задач,
работа с неопределенной и неполной информацией.
Удобно считать, что экспертная система со стоит из двух модулей: оболочки и базы знаний. Оболочка в свою очередь состоит из механизма логического вывода и интерфейса с пользователем. При создании экспертной системы необходимо принять решения о выборе формального языка представления знаний, механизма логического вывода, средств взаимодействия с пользователем и способа работы в условиях неопределенности. "Если-то"-правила, или продукции являются наиболее часто применяемой формой представ ления знаний в экспертных системах. Оболочка, разработанная в данной главе, интерпретирует "если-то"-правила, обеспечивает выдачу объяснений типа "как" и "почему" и запрашивает у пользователя необходимую информацию. Машина логического вывода была расширена для работы с неопределенной информацией. В данной главе были обсуждены следующие понятия:
экспертные системы
база знаний, оболочка,
машина логического вывода
"если-то"-правила, продукции
объяснения типа "как" и "почему"
категорические знания, неопределенные знания
сеть вывода,
распространение оценок достоверности по сети
Игры двух лиц поддаются формальному
Игры двух лиц поддаются формальному представлению в виде И / ИЛИ-графов. Поэтому процедуры поиска в И / ИЛИ-графах применимы для поиска в игровых деревьях. Простой алгоритм поиска в глубину в игровых деревьях легко программируется, но для игр, представляющих интерес, он не эффективен. Более реалистичный подход - минимаксный принцип в сочетании с оценочной функцией и поиском, ограниченным по глубине. Альфа-бета алгоритм является эффективной реализацией минимаксного принципа. Эффективность альфа-бета алгоритма зависит от порядка, в котором просматриваются варианты ходов. Применение альфа-бета алгоритма приводит, в лучшем случае, к уменьшению коэффициента ветвления дерева поиска, соответствующему извлечению из него квадратного корня. В альфа-бета алгоритм можно внести ряд усовершенствований. Среди них: продолжение поиска за пределы ограничения по глубине вплоть до спокойных позиций, последовательное углубление и эвристическое отсечение ветвей. Численная оценка позиций является весьма ограниченной формой представления знаний о конкретной игре. Более богатый по своим возможностям метод представления знаний должен предусматривать внесение в программу знаний о типовых ситуациях. Язык Советов (Advice Language) реализует такой подход. На этом языке знания представляются в терминах целей и средств для их достижения. В даннной главе мы составили следующие программы: программная реализация минимаксного принципа и альфа-бета процедуры, интерпретатор языка AL0 и таблица советов для окончания "король и ладья против короля". Были введены и обсуждены следующие понятия:
игры двух лиц с полной информацией
игровые деревья
оценочная функция, минимаксный принцип
статические оценки, рабочие оценки
альфа-бета алгоритм
последовательное углубление,
эвристическое отсечение,
эвристики для обнаружения спокойных позиций
Языки Советов
цели, ограничения, элементарные советы,
таблица советов
хорошо приспособлена для решения многих
Архитектура, ориентированная на типовые конфигурации (образцы), хорошо приспособлена для решения многих задач искусственного интеллекта. Программа, управляемая образцами, состоит из модулей, запускаемых при возникновении в базе данных тех или иных конфигураций. Прологовские программы можно рассматривать как частный случай систем, управляемых образцами. Параллельная реализация - наиболее естественный способ реализации систем, управляемых образцами. Реализация на последовательной машине требует разрешения конфликтов между модулями, содержащимися в конфликтном множестве. В этой главе был реализован простой интерпретатор для программ, управляемых образцами. Он был затем применен к задаче автоматического доказательства теорем пропозициональной логики. Были рассмотрены следующие понятия:
системы, управляемые образцами
архитектуры, ориентированные на образцы
программирование в терминах образцов
модули, управляемые образцами
конфликтное множество, разрешение конфликтов
принцип резолюции
автоматическое доказательство теорем на
основе принципа резолюции
К настоящему моменту мы изучили
К настоящему моменту мы изучили нечто вроде базового Пролога, который называют еще "чистый Пролог". Он "чист", потому что довольно точно соответствует формальной логике. Расширения, преследующие цель приспособить язык к некоторым практическим нуждам, будут изучены дальше (гл. 3, 5, 6. 7). Важными моментами данной главы являются следующие: Простые объекты в Прологе - это атомы, переменные и числа. Структурные объекты, или структуры, используются для представления объектов, которые состоят из нескольких компонент. Структуры строятся посредством функторов. Каждый функтор определяется своими именем и арностью. Тип объекта распознается исключительно по его синтаксической форме. Область известности (лексический диапазон) переменных - одно предложение. Поэтому одно и то же имя в двух предложениях обозначает две разные переменные. Структуры могут быть естественным образом изображены в виде деревьев. Пролог можно рассматривать как язык обработки деревьев. Операция сопоставление берет два терма и пытается сделать их идентичными, подбирая соответствующую конкретизацию переменных в обоих термах. Сопоставление, если оно завершается успешно, в качестве результата выдает наиболее общую конкретизацию переменных. Декларативная семантика Пролога определяет, является ли целевое утверждение истинным, исходя из данной программы, и если оно истинно, то для какой конкретизации переменных. Запятая между целями означает их конъюнкцию. Точка с запятой между целями означает их дизъюнкцию. Процедурная семантика Пролога - это процедура достижения списка целей в контексте данной программы. Процедура выдает истинность или ложность списка целей и соответствующую конкретизацию переменных. Процедура осуществляет автоматический возврат для перебора различных вариантов. Декларативный смысл программ на "чистом Прологе" не зависит от порядка предложений и от порядка целей в предложениях. Процедурный смысл существенно зависит от порядка целей и предложений. Поэтому порядок может повлиять на эффективность программы; неудачный порядок может даже привести к бесконечным рекурсивным вызовам. Имея декларативно правильную программу, можно улучшить ее эффективность путем изменения порядка предложений и целей при сохранении ее декларативной правильности. Переупорядочивание - один из методов предотвращения зацикливания. Кроме переупорядочивания существуют и другие, более общие методы предотвращения зацикливания, способствующие получению процедурно правильных программ. В данной главе обсуждались следующие понятия:
объекты данных:
атом, число, переменная, структура
терм
функтор, арность функтора
главный функтор терма
сопоставление термов
наиболее общая конкретизация
декларативная семантика
конкретизация предложений,
вариант предложения
процедурная семантика
вычисление целевого утверждения
