Формирование оптимального пространства признаков

В типичной ситуации набор выходных, прогнозируемых, переменных фиксирован, и требуется подобрать наилучшую комбинацию ограниченного числа входных величин. Оценка значимости входов позволяет построить процедуру систематического предварительного подбора входных переменных - до этапа обучения нейросети. Для иллюстрации опишем две возможные стратеги автоматического формирования признакого пространства.

Формирование признакого пространства методом ортогонализации

Следующая систематическая процедура способна итеративно выделять наиболее значимые признаки, являющиеся линейными комбинациями входных переменных:

(подмножество входов является частным случаем линейной комбинации, т.е. формально можно найти лучшее решение, чем то, что доступно путем отбора наиболее значимых комбинаций входов).

Рис. 7.15.  Выбор наиболее значимых линейных комбинаций входных переменных

Для определения значимости каждой входной компоненты будем использовать каждый раз индивидуальную значимость этого входа:

.

Подсчитав индивидуальную значимость входов, находим направление в исходном входном пространстве, отвечающее наибольшей (нелинейной) чувствительности выходов к изменению входов. Это градиентное направление определит первый вектор весов, дающий первую компоненту пространства признаков:

Следующую компоненту будем искать аналогично первой, но уже в пространстве перпендикулярном выбранному направлению, для чего спроектируем все входные вектора в это пространство:

В этом пространстве можно опять подсчитать "градиент" предсказуемости, определив индивидуальную значимость спроектированных входов, и так далее. На каждом следующем этапе подсчитывается индивидуальная значимость

для проекции входов , что не требует повышения размерности box-counting анализа. Таким образом, описанная выше процедура позволяет формировать пространство признаков произвольной размерности - без потери точности.

Индивидуальная нормировка данных

Приведение данных к единичному масштабу обеспечивается нормировкой каждой переменной на диапазон разброса ее значений. В простейшем варианте это - линейное преобразование:

в единичный отрезок:

. Обобщение для отображения данных в интервал , рекомендуемого для входных данных тривиально.

Линейная нормировка оптимальна, когда значения переменной

плотно заполняют определенный интервал. Но подобный "прямолинейный" подход применим далеко не всегда. Так, если в данных имеются относительно редкие выбросы, намного превышающие типичный разброс, именно эти выбросы определят согласно предыдущей формуле масштаб нормировки. Это приведет к тому, что основная масса значений нормированной переменной сосредоточится вблизи нуля: .

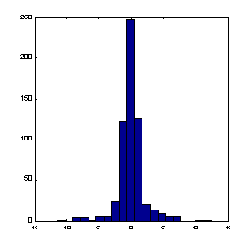
Рис. 7.2.  Гистограмма значений переменной при наличии редких, но больших по амплитуде отклонений от среднего

Гораздо надежнее, поэтому, ориентироваться при нормировке не на экстремальные значения, а на типичные, т.е. статистические характеристики данных, такие как среднее и дисперсия:

В этом случае основная масса данных будет иметь единичный масштаб, т.е. типичные значения всех переменных будут сравнимы (см. рисунок 7.2).

Однако, теперь нормированные величины не принадлежат гарантированно единичному интервалу, более того, максимальный разброс значений

. заранее не известен. Для входных данных это может быть и не важно, но выходные переменные будут использоваться в качестве эталонов для выходных нейронов. В случае, если выходные нейроны - сигмоидные, они могут принимать значения лишь в единичном диапазоне. Чтобы установить соответствие между обучающей выборкой и нейросетью в этом случае необходимо ограничить диапазон изменения переменных.

Линейное преобразование, как мы убедились, неспособно отнормировать основную массу данных и одновременно ограничить диапазон возможных значений этих данных. Естественный выход из этой ситуации - использовать для предобработки данных функцию активации тех же нейронов. Например, нелинейное преобразование

нормирует основную массу данных одновременно гарантируя, что (см. рисунок 7.3).


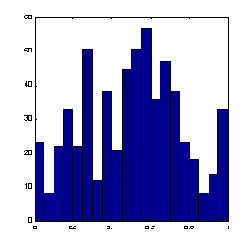
Рис. 7.3.  Нелинейная нормировка, использующая логистическую функцию активации

Как видно из приведенного выше рисунка, распределение значений после такого нелинейного преобразования гораздо ближе к равномерному.

До сих пор мы старались максимизировать энтропию каждого входа (выхода) по отдельности. Но, вообще говоря, можно добиться гораздо большего максимизируя их совместную энтропию. Рассмотрим эту технику на примере совместной нормировки входов, подразумевая, что с таким же успехом ее можно применять и для выходов а также для всей совокупности входов-выходов.

Кодирование категориальных переменных

В принципе, категориальные переменные также можно закодировать описанным выше способом, пронумеровав их произвольным образом. Однако, такое навязывание несуществующей упорядоченности только затруднит решение задачи. Оптимальное кодирование не должно искажать структуры соотношений между классами. Если классы не упорядоченны, такова же должна быть и схема кодирования.

Наиболее естественной выглядит и чаще всего используется на практике двоичное кодирование типа

, когда имена категорий кодируются значениями бинарных нейронов, причем первая категория кодируется как , вторая, соответственно - и т.д. вплоть до -ной: . (Можно использовать биполярную кодировку, в которой нули заменяются на ). Легко убедиться, что в такой симметричной кодировке расстояния между всеми векторами-категориями равны.

Такое кодирование, однако, неоптимально в случае, когда классы представлены существенно различающимся числом примеров. В этом случае, функция распределения значений переменной крайне неоднородна, что существенно снижает информативность этой переменной. Тогда имеет смысл использовать более компактный, но симметричный код

, когда имена классов кодируются -битным двоичным кодом. Причем, в новой кодировке активность кодирующих нейронов должна быть равномерна: иметь приблизительно одинаковое среднее по примерам значение активации. Это гарантирует одинаковую значимость весов, соответствующих различным нейронам.

В качестве примера рассмотрим ситуацию, когда один из четырех классов (например, класс

) некой категориальной переменной представлен гораздо большим числом примеров, чем остальные: . Простое кодирование привело бы к тому, что первый нейрон активировался бы гораздо чаще остальных. Соответственно, веса оставшихся нейронов имели бы меньше возможностей для обучения. Этой ситуации можно избежать, закодировав четыре класса двумя бинарными нейронами следующим образом: , обеспечивающим равномерную "загрузку" кодирующих нейронов.

Кодирование ординальных переменных

Ординальные переменные более близки к числовой форме, т.к. числовой ряд также упорядочен. Соответственно, для кодирования таких переменных остается лишь поставить в соответствие номерам категорий такие числовые значения, которые сохраняли бы существующую упорядоченность. Естественно, при этом имеется большая свобода выбора - любая монотонная функция от номера класса порождает свой способ кодирования. Какая же из бесконечного многообразия монотонных функций - наилучшая?

В соответствии с изложенным выше общим принципом, мы должны стремиться к тому, чтобы максимизировать энтропию закодированных данных. При использовании сигмоидных функций активации все выходные значения лежат в конечном интервале - обычно

или . Из всех статистических функций распределения, определенных на конечном интервале, максимальной энтропией обладает равномерное распределение.

Применительно к данному случаю это подразумевает, что кодирование переменных числовыми значениями должно приводить, по возможности, к равномерному заполнению единичного интервала закодированными примерами. (Захватывая заодно и этап нормировки.) При таком способе "оцифровки" все примеры будут нести примерно одинаковую информационную нагрузку.

Исходя из этих соображений, можно предложить следующий практический рецепт кодирования ординальных переменных. Единичный отрезок разбивается на отрезков - по числу классов - с длинами пропорциональными числу примеров каждого класса в обучающей выборке:

, где - число примеров класса , а , как обычно, общее число примеров. Центр каждого такого отрезка будет являться численным значением для соответствующего ординального класса (см. рисунок 7.1).

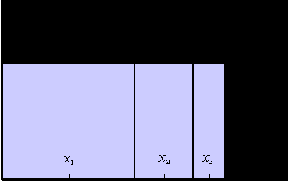
Рис. 7.1.  Илюстрация способа кодирования кардинальных переменных с учетом количества примеров каждой категории

Кодирование входов-выходов

В отличие от обычных компьютеров, способных обрабатывать любую символьную информацию, нейросетевые алгоритмы работают только с числами, ибо их работа базируется на арифметических операциях умножения и сложения. Именно таким образом набор синаптических весов определяет ход обработки данных.

Между тем, не всякая входная или выходная переменная в исходном виде может иметь численное выражение. Соответственно, все такие переменные следует закодировать - перевести в численную форму, прежде чем начать собственно нейросетевую обработку. Рассмотрим, прежде всего основной руководящий принцип, общий для всех этапов предобработки данных.

Квантование входов

Более распространенный вид нейросетевой предобработки данных - квантование входов, использующее слой соревновательных нейронов (см. рисунок 7.9).

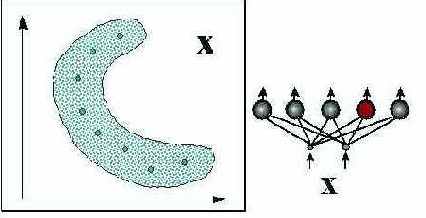
Рис. 7.9.  Понижение разнообразия входов методом квантования (кластеризации)

Нейрон-победитель является прототипом ближайших к нему входных векторов. Квантование входов обычно не сокращает, а наоборот, существенно увеличивает число входных переменных. Поэтому его используют в сочетании с простейшим линейным дискриминатором - однослойным персептороном. Получающаяся в итоге гибридная нейросеть, предложенная Нехт-Нильсеном в 1987 году, обучается послойно: сначала соревновательный слой кластеризует входы, затем выходным весам присваиваются значения выходной функции, соответствующие данному кластеру. Такие сети позволяют относительно быстро получать грубое - кусочно-постоянное - приближение аппроксимируемой функции (см. рисунок 7.10).

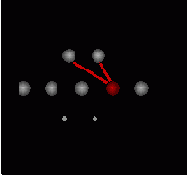
Рис. 7.10.  Гибридная сеть с соревновательным слоем, дающая кусочно-постоянное приближение функций

Особенно полезны кластеризующие сети для восстановления пропусков в массиве обучающих данных. Поскольку работа соревновательного слоя основана на сравнении расстояний между данными и прототипами, осутствие у входного вектора

некоторых компонент не препятствует нахождению прототипа-победителя: сравнение ведется по оставшимся компонентам :

При этом все прототипы

находятся в одинаковом положении. Рисунок 7.11 иллюстрирует эту ситуацию.

Рис. 7.11.  Наличие пропущенных компонент не препятствует нахождению ближайшего прототипа по оставшимся компонентам входного вектора

Таким образом, слой квантующих входные данные нейронов нечувствителен к пропущенным компонентам, и может служить "защитным экраном" для минимизации последствий от наличия пропусков в обучающей базе данных.

Линейная значимость входов

Легче всего оценить значимость входов в линейной модели, предполагающей линейную зависимость выходов от входов:

Матрицу весов

можно получить, например, обучением простейшего - однослойного персептрона с линейной функцией активации. Допустим теперь, что при определении выходов мы опускаем одну, для определенности - -ю компоненту входов, заменяя ее средним значением этой переменной. Это приведет к огрублению модели, т.е. возрастании ошибки на величину:

(Полагая, что данные нормированны на их дисперсию.) Таким образом, значимость

-го входа определяется суммой квадратов соответствующих ему весов.

Особенно просто определить значимость выбеленных входов. Для достаточно просто вычислить взаимную корреляцию входов и выходов:

Действительно, при линейной зависимости между входами и выходами имеем:

Таким образом, в общем случае для получения матрицы весов требуется решить систему линейных уравнений. Но для предварительно выбеленных входов имеем:

, так что в этом случае матрица кросс-корреляций просто совпадает с матрицей весов обученного линейного персептрона: .

Резюмируя, значимость входов в предположении о приблизительно линейной зависимости между входными и выходными переменными для выбеленных входов пропорциональна норме столбцов матрицы кросс-корреляций:

.

Не следует, однако, обольщаться существованием столь простого рецепта определения значимости входов. Линейная модель может быть легко построена и без привлечения нейросетей. Реальная сила нейроанализа как раз и состоит в возможности находить более сложные нелинейные зависимости. Более того, для облегчения собственно нелинейного анализа рекомендуется заранее освободиться от тривиальных линейных зависимостей - т.е. в качестве выходов при обучении подавать разность между выходными значениями и их линейным приближением. Это увеличит "разрешающую способность" нейросетевого моделирования (см. рисунок 7.12).

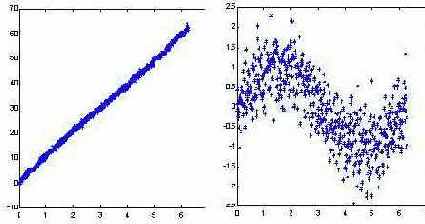
Рис. 7.12.  Выявление нелинейной составляющей функции после вычитания линейной зависимости . ( Здесь - гауссовый случайный шум)

Для определения "нелинейной" значимости входов - после вычитания линейной составляющей, изложенный выше подход неприменим. Здесь надо привлекать более изощренные методики. К описанию одной из них, алгоритмам box-counting, мы и переходим.

Максимизация энтропии как цель предобработки

Допустим, что в результате перевода всех данных в числовую форму и последующей нормировки все входные и выходные переменные отображаются в единичном кубе. Задача нейросетевого моделирования - найти статистически достоверные зависимости между входными и выходными переменными. Единственным источником информации для статистического моделирования являются примеры из обучающей выборки. Чем больше бит информации принесет каждый пример - тем лучше используются имеющиеся в нашем распоряжения даные.

Рассмотрим произвольную компоненту нормированных (предобработанных) данных:

. Среднее количество информации, приносимой каждым примером , равно энтропии распределения значений этой компоненты . Если эти значения сосредоточены в относительно небольшой области единичного интервала, информационное содержание такой компоненты мало. В пределе нулевой энтропии, когда все значения переменной совпадают, эта переменная не несет никакой информации. Напротив, если значения переменной равномерно распределены в единичном интервале, информация такой переменной максимальна.

Общий принцип предобработки данных для обучения, таким образом, состоит в максимизации энтропии входов и выходов. Этим принципом следует руководствоваться и на этапе кодирования нечисловых переменных.

Нелинейная значимость входов. Box-counting алгоритмы

Алгортимы box-counting, как следует из самого их названия, основаны на подсчете чисел заполнения примерами

ячеек (boxes), на которые специально для этого разбивается пространство переменных . Эти числа заполнения используются для оценки плотности вероятности распределения примеров по ячейкам. Набор вероятностей дает возможность рассчитать любую статистическую характеристику набора данных обучающей выборки.

Для определения значимости входов нам потребуется оценить предсказуемость выходов, обеспечиваемую данным набором входных переменных. Чем выше эта предсказуемость - тем лучше соответствующий набор входов. Таким образом, метод box-counting предоставляет в наше распоряжение технологию отбора наиболее значимых признаков для нейросетевого моделирования, технологию оптимизации входного пространства признаков.

Согласно общим положениям теории информации, мерой предсказуемости случайной величины

является ее энтропия, , определяемая как среднее значение ее логарифма. В методике box-counting энтропия приближенно оценивается по набору чисел заполнения ячеек, на которые разбивается интервал ее возможных значений: . Качественно, энтропия есть логарифм эффективного числа заполненных ячеек (см. рисунок 7.13). Чем больше энтропия переменной, тем менее предсказуемо ее значение. Когда все значения примеров сосредоточены в одной ячейке - их энтропия равна нулю, т.к. положение данных определено (с данной степенью точности). Равномерному заполнению ячеек соответствует максимальная энтропия - наибольший разброс возможных значений переменной.

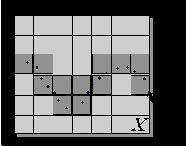
Рис. 7.13.  Смысл энтропии - эффективное число заполненных данными ячеек

Предсказуемость случайного вектора

, обеспечиваемое знанием другой случайной величины , дается кросс-энтропией:

Качественно, кросс-энтропия равна логарифму отношения типичного разброса значений переменной

к типичному разбросу этой переменной, но при известном значении переменной (см. рисунок 7.14):

Рис. 7.14.  Иллюстрация к понятию кросс-энтропии: - полное число ячеек в объединенном пространстве , - число проекций ячеек на пространство , - характерный разброс по оси при фиксированном , - характерный разброс всех данных по jcb

Чем больше кросс-энтропия, тем больше определенности вносит знание значения в предсказание значения переменной .

Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными. Таким образом, данная методика дает наиболее общий рецепт определения значимости входов, позволяя также оценивать степень предсказуемости выходов.

В принципе, качество предсказаний и, соответственно, значимость входной информации определяется, в конечном итоге, в результате обучения нейросети, которая, к тому же, дает решение в явном виде. Однако, как мы знаем, обучение нейросети - довольно сложная вычислительная задача (требующая операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с вычислительной сложностью ), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу предварительного отбора входной информации на этапе предобработки данных.




Чем больше кросс-энтропия, тем больше определенности вносит знание значения в предсказание значения переменной .

Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными. Таким образом, данная методика дает наиболее общий рецепт определения значимости входов, позволяя также оценивать степень предсказуемости выходов.

В принципе, качество предсказаний и, соответственно, значимость входной информации определяется, в конечном итоге, в результате обучения нейросети, которая, к тому же, дает решение в явном виде. Однако, как мы знаем, обучение нейросети - довольно сложная вычислительная задача (требующая операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с вычислительной сложностью ), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу предварительного отбора входной информации на этапе предобработки данных.

Необходимые этапы нейросетевого анализа

Теперь, после знакомства с базовыми принципами нейросетевой обработки, можно приступать к практическим применениям полученных знаний для решения конкретных задач. Первое, с чем сталкивается пользователь любого нейропакета - это необходимость подготовки данных для нейросети. До сих пор мы не касались этого, вообще говоря, непростого вопроса, молчаливо предполагая, что данные для обучения уже имеются и представлены в виде, доступном для нейросети. На практике же именно предобработка данных может стать наиболее трудоемким элементом нейросетевого анализа. Причем, знание основных принципов и приемов предобработки данных не менее, а может быть даже более важно, чем знание собственно нейросетевых алгоритмов. Последние как правило, уже "зашиты" в различных нейроэмуляторах, доступных на рынке. Сам же процесс решения прикладных задач, в том числе и подготовка данных, целиком ложится на плечи пользователя. Данная лекция призвана заполнить этот пробел в описании технологии нейросетевого анализа.

Для начала выпишем с небольшими комментариями всю технологическую цепочку, т.е. необходимые этапы нейросетевого анализа: 1)

Кодирование входов-выходов: нейросети могут работать только с числами. Нормировка данных: результаты нейроанализа не должны зависеть от выбора единиц измерения. Предобработка данных: удаление очевидных регулярностей из данных облегчает нейросети выявление нетривиальных закономерностей. Обучение нескольких нейросетей с различной архитектурой: результат обучения зависит как от размеров сети, так и от ее начальной конфигурации. Отбор оптимальных сетей: тех, которые дадут наименьшую ошибку предсказания на неизвестных пока данных. Оценка значимости предсказаний: оценка ошибки предсказаний не менее важна, чем само предсказанное значение.

Если до сих пор мы ограничивали наше рассмотрение, в основном, последними этапами, связанными с обучением собственно нейросетей, то в этой лекции мы сосредоточимся на первых этапах нейросетевого анализа - предобработке данных. Хотя перобработка не связана непосредственно с нейросетями, она является одним из ключевых элементов этой информационной технологии. Успех обучения нейросети может решающим образом зависеть от того, в каком виде представлена информация для ее обучения.

В этой лекции мы рассмотрим предобработку данных для обучения с учителем и постараемся, главным образом, выделить и проиллюстрировать на конкретных примерах основной принцип такой предобработки: увеличение информативности примеров для повышения эффективности обучения.

Нормировка и предобработка данных

Как входами, так и выходами нейросети могут быть совершенно разнородные величины. Очевидно, что результаты нейросетевого моделирования не должны зависеть от единиц измерения этих величин. А именно, чтобы сеть трактовала их значения единообразно, все входные и выходные величины должны быть приведены к единому - единичному - масштабу. Кроме того, для повышения скорости и качества обучения полезно провести дополнительную предобработку данных, выравнивающую распределение значений еще до этапа обучения.

Отбор наиболее значимых входов

До сих пор мы старались лишь представить имеющуюся входную информацию наилучшим - наиболее информативным - образом. Однако, рассмотренные выше методы предобработки входов никак не учитывали зависимость выходов от этих входов. Между тем, наша задача как раз и состоит в выборе входных переменных, наиболее значимых для предсказаний. Для такого более содержательного отбора входов нам потребуются методы, позволяющие оценивать значимость входов.

Отличие между входными и выходными переменными

В заключении данного раздела отметим одно существенное отличие способов кодирования входных и выходных переменных, вытекающее из определения градиента ошибки:

. А именно, входы участвуют в обучении непосредственно, тогда как выходы - лишь опосредованно - через ошибку верхнего слоя. Поэтому при кодировании категорий в качестве выходных нейронов можно использовать как логистическую функцию активации , определенную на отрезке , так и ее антисимметричный аналог для отрезка , например: . При этом кодировка выходных переменных из обучающей выборки будет либо , либо . Выбор того или иного варианта никак не скажется на обучении.

В случае со входными переменными дело обстоит по-другому: обучение весов нижнего слоя сети определяется непосредственно значениями входов: на них умножаются невязки, зависящие от выходов. Между тем, если с точки зрения операции умножения значения

равноправны, между 0 и 1 имеется существенная асимметрия: нулевые значения не дают никакого вклада в градиент ошибки. Таким образом, выбор схемы кодирования входов влияет на процесс обучения. В силу логической равноправности обоих значений входов, более предпочтительной выглядит симметричная кодировка: , сохраняющая это равноправие в процессе обучения.

Понижение размерности входов

Сильной стороной нейроанализа является возможность получения предсказаний при минимуме априорных знаний. Поскольку заранее обычно неизвестно насколько полезны те или иные входные переменные для предсказания значений выходов, возникает соблазн увеличивать число входных параметров, в надежде на то, что сеть сама определит какие из них наиболее значимы. Однако, как это уже обсуждалось в лекции 3, сложность обучения персептронов быстро возрастает с ростом числа входов (а именно - как куб размерности входных данных

). Еще важнее, что с увеличением числа входов страдает и точность предсказаний, т.к. увеличение числа весов в сети снижает предсказательную способность последней (согласно предыдущим оценкам: ).

Таким образом, количество входов приходится довольно жестко лимитировать, и выбор наиболее информативных входных переменных представляет важный этап подготовки данных для обучения нейросетей. Лекция 4 специально посвящена использованию для этой цели самих нейросетей, обучаемых без учителя. Не стоит, однако, пренебрегать и традиционными, более простыми и зачастую весьма эффективными методами линейной алгебры.

Один из наиболее простых и распространенных методов понижения размерности - использование главных компонент входных векторов. Этот метод позволяет не отбрасывая конкретные входы учитывать лишь наиболее значимые комбинации их значений.

Понижение размерности входов методом главных компонент

Собственные числа матрицы ковариаций

, фигурировавшие в предыдущем разделе, являются квадратами дисперсий вдоль ее главных осей. Если между входами существует линейная зависимость, некоторые из этих собственных чисел стремятся к нулю. Таким образом, наличие малых свидетельствует о том, что реальная размерность входных данных объективно ниже, чем число входов. Можно задаться некоторым пороговым значением и ограничиться лишь теми главными компонентами, которые имеют . Тем самым, достигается понижение размерности входов, при минимальных потерях точности представления входной информации.

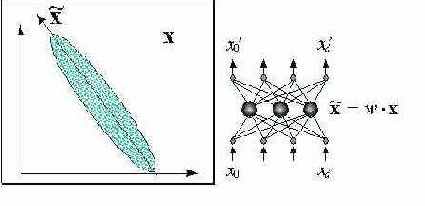
Рис. 7.5.  Понижение размерности входов методом главных компонент

Понижение размерности входов с помощью нейросетей

Для более глубокой предобработки входов можно использовать все богатство алгоритмов самообучающихся нейросетей, о которых шла речь ранее. В частности, для оптимального понижения размерности входов можно воспользоваться методом нелинейных главных компонент (см. рисунок 7.7).

Рис. 7.7.  Понижение размерности входов методом нелинейных главных компонент

Такие сети с узким горлом также можно использовать для восстановления пропущенных значений - с помощью итерационной процедуры, обобщающей линейный вариант метода главных компонент (см. рисунок 7.8).

Рис. 7.8.  Восстановление пропущенных компонент данных с помощью нелинейных главных компонент

Однако, такую глубокую "предобработку" уже можно считать самостоятельной нейросетевой задачей. И мы не будем дале углубляться в этот вопрос.

Последовательное добавление наиболее значимых входов

Один из наиболее очевидных способов формирования пространства признаков с учетом реальной значимости входов - постепенный подбор наиболее значимых входов в качестве очередных признаков. В качестве первого признака выбирается вход с наибольшей индивидуальной значимостью:

Вторым признаком становится вход, обеспечивающий наибольшую предсказуемость в паре с уже выбранным:

и так далее. На каждом следующем этапе добавляется вход, наиболее значимый в компании с выбранными ранее входами:

Такая процедура не гарантирует нахождения наилучшей комбинации входов, т.е. дает субоптимальный набор признаков, т.к. реально рассматривается лишь очень малая доля от полного числа комбинаций входов, и значимость каждого нового признака зависит от сделанного прежде выбора. Полный перебор, однако, практически неосуществим: выбор оптимальной комбинации входов при полном их числе

требует перебора комбинаций.

Другим недостатком описанного выше подхода является необходимость подсчета кросс-энтропии в пространстве все более высокой размерности по мере увеличения числа отобранных признаков. Ниже описана процедура, свободная от этого недостатка, основанная на применении методики box-counting лишь в низкоразмерных пространствах (а именно - с размерностью

).

Совместная нормировка: выбеливание входов

Если два входа статистически не независимы, то их совместная энтропия меньше суммы индивидуальных энтропий:

. Поэтому добившись статистической независимости входов мы, тем самым, повысим информационную насыщенность входной информации. Это, однако, потребует более сложной процедуры совместной нормировки входов.

Вместо того, чтобы использовать для нормировки индивидуальные дисперсии, будем рассматривать входные данные в совокупности. Мы хотим найти такое линейное преобразование, которое максимизировало бы их совместную энтропию. Для упрощения задачи вместо более сложного условия статистической независимости потребуем, чтобы новые входы после такого преобразования были декоррелированы . Для этого рассчитаем средний вектор и ковариационную матрицу данных по формулам:

Затем найдем линейное преобразование, диагонализующее ковариационную матрицу. Соответствующая матрица составлена из столбцов - собственных векторов ковариационной матрицы:

Легко убедиться, что линейное преобразование, называемое выбеливанием (whitening)

превратит все входы в некоррелированные величины с нулевым средним и единичной дисперсией.

Если входные данные представляют собой многомерный эллипсоид, то графически выбеливание выглядит как растяжение этого эллипсоида по его главным осям ( рисунок 7.4).

Рис. 7.4.  Выбеливание входной информации: повышение информативности входов за счет выравнивания функции распределения

Очевидно, такое преобразование увеличивает совместную энтропию входов, т.к. оно выравнивает распределение данных в обучающей выборке.

Типы нечисловых переменных

Можно выделить два основных типа нечисловых переменных: упорядоченные (называемые также ординальными - от англ. order - порядок) и категориальные. В обоих случаях переменная относится к одному из дискретного набора классов

. Но в первом случае эти классы упорядочены - их можно ранжировать: , тогда как во втором такая упорядоченность отсутствует. В качестве примера упорядоченных переменных можно привести сравнительные категории: плохо - хорошо - отлично, или медленно - быстро. Категориальные переменные просто обозначают один из классов, являются именами категорий. Например, это могут быть имена людей или названия цветов: белый, синий, красный.

Восстановление пропущенных компонент данных

Главные компоненты оказываются удобным инструментом и для восстановления пропусков во входных данных. Действительно, метод главных компонент дает наилучшее линейное приближение входных данных меньшим числом компонент:

(Здесь мы, как и прежде, для учета постоянного члена включаем фиктивную нулевую компоненту входов, всегда равную единице - см. рисунок 7.5, где справа показана нейросетевая интерпретация метода главных компонент. Таким образом, - это матрица размерности ). Восстановленные по главным компонентам данные из обучающей выборки имеют наименьшее среднеквадратичное отклонение от своих прототипов . Иными словами, при отсутствии у входного вектора компонент, наиболее вероятное положение этого вектора - на гиперплоскости первых главных компонент. Таким образом, для восстановленного вектора имеем: , причем для известных компонент .

Пусть, например, у вектора

неизвестна всего одна, -я координата. Ее значение находится из оставшихся по формуле:

где в числителе учитываются лишь известные компоненты входного вектора

.

В общем случае восстановить неизвестные компоненты (с индексами из множества

) можно с помощью следующей итеративной процедуры (см. рисунок 7.6):

Рис. 7.6.  Восстановление пропущенных значения с помощью главных компонент. Пунктир - возможные значения исходного вектора с неизвестными координатами. Наиболее вероятное его значение - на пересечении с первыми главными компонентами

описанными выше методиками не исчерпывается

Конечно, описанными выше методиками не исчерпывается все разнообразие подходов к ключевой для нейро-анализа проблеме формирования пространства признаков. Мы не упомянули, в частности, генетические алгоритмы, которые в совокупностью с методикой box-counting являются весьма перспективным инструментом. Ничего не было сказано также о методике разделения независимых компонент (blind signal separation), расширяющей анализ главных компонент. Необъятного не объять. Главное, чтобы за деталями не затерялся основополагающий принцип предобработки данных: снижение существующей избыточности всеми возможными способами. Это повышает информативность примеров и, тем самым, качество нейропредсказаний.

Формирование пространства признаков

Ключевым для повышения качества предсказаний является эффективное кодирование входной информации. Это особенно важно для труднопредсказуемых финансовых временных рядов. Все рекомендации, описанные в лекции о предобработке данных, применимы и здесь. Имеются, однако, и специфичные именно для финансовых временных рядов способы предобработки данных, на которых мы подробно остановимся в данном разделе.

Формирование входного пространства признаков

Как иллюстрирует рисунок 8.5, увеличение ширины окна погружения ряда приводит в конце концов к понижению предсказуемости - когда повышение размерности входов уже не компенсируется увеличением их информативности. В этом случае, когда размерность лагового пространства слишком велика для данного количества примеров, приходится применять специальные методики формирования пространства признаков с меньшей размерностью. Способы выбора признаков и/или увеличения числа доступных примеров, специфичные для финансовых временных рядов будут описаны ниже.

Использование комитетов сетей

Из-за случайности в выборе начальных значений синаптических весов, предсказания сетей, обученных на одной и той же выборке, будут, вообще говоря, разниться. Этот недостаток (элемент неопределенности) можно превратить в достоинство, организовав комитет нейро-экспертов, состоящий из различных нейросетей. Разброс в предсказаниях экспертов даст представление о степени уверенности этих предсказаний, что можно использовать для правильного выбора стратегии игры.

Легко показать, что среднее значений комитета должно давать лучшие предсказания, чем средний эксперт из этого же комитета. Пусть ошибка

-ого эксперта для значения входа равна . Средняя ошибка комитета всегда меньше среднеквадратичной ошибки отдельных экспертов в силу неравенства Коши:

Причем, снижение ошибки может быть довольно заметным. Так, если ошибки отдельных экспертов не коррелируют друг с другом, т.е.

, то среднеквадратичная ошибка комитета из экспертов в раз меньше, чем средняя индивидуальная ошибка одного эксперта!

Поэтому, в предсказаниях всегда лучше опираться на средние значения всего комитета. Иллюстрацией этого факта служит рисунок 8.12.

Рис. 8.12.  Норма прибыли на последних 100 значениях ряда sp500 при предсказании комитетом из 10 сетей. Выигрыш комитета (кружки) выше, чем выигрыш среднего эксперта. Счет угаданных знаков для комитета 59:41

Как видно из приведенного выше рисунка, в данном случае выигрыш комитета даже выше, чем выигрыш каждого из экспертов. Таким образом, метод комитетов может существенно повысить качество прогнозирования. Обратите внимание на абсолютное значение нормы прибыли: капитал комитета возрос в 3.25 раза при 100 вхождениях в рынок (Естественно, эта норма будет ниже при учете транзакционных издержек).

Предсказания получены при обучении сети на 30 последовательных экспоненциальных скользящих средних (EMA1 … EMA30) ряда приращений индекса. Предсказывался знак приращения на следующем шаге.

В этом эксперименте ставка была зафиксирована на уровне

, близком к оптимальному при данной точности предсказаний (59 угаданных знаков против 41 ошибки) т.е. .
На следующем же рисунке приведены результаты более рискованной игры по тем же предсказаниям, а именно - с .
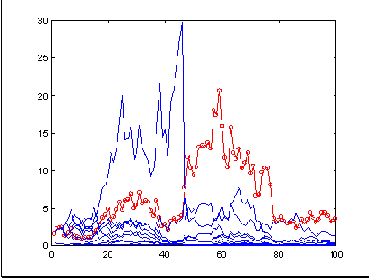
Рис. 8.13.  Норма прибыли на последних 100 значениях ряда sp500 при тех же предсказаниях комитета из 10 сетей, но по более рискованной стратегии

Выигрыш комитета в целом остался на прежнем уровне (чуть увеличился), поскольку данное значение риска так же близко к оптимуму, как и предыдущее. Однако, для большинства сетей, предсказания которых хуже, чем у комитета в целом, такие ставки оказались слишком рискованными, что привело к практически полному их разорению.

Приведенные выше примеры показывают как важно уметь правильно оценить качество предсказания и как можно использовать эту оценку для увеличения прибыльности от одних и тех же предсказаний.

Можно пойти еще дальше и вместо среднего использовать взвешенное мнение сетей-экспертов. Веса выбираются адаптивно максимизируя предсказательную способность комитета на обучающей выборке. В итоге, хуже обученные сети из комитета вносят меньший вклад и не портят предсказания.

Возможности этого пути иллюстрирует приведенное ниже сравнение предсказаний двух типов комитетов из 25 экспертов (см. рисунки 8.14,8.15). Предсказания проводились по одной и той же схеме: в качестве входов использовались экспоненциальные скользящие средние приращений ряда с периодами равными первым 10 числам Фибоначчи. По результатам 100 экспериментов взвешенное предсказание дает в среднем превышение правильно угаданных знаков над ошибочным равное примерно 15, тогда как среднее - около 12. Заметим, что общее число повышений курса над понижением за указанный период как раз равно 12. Следовательно, учет общей тенденции к повышению в виде тривиального постоянного предсказания знака "+" дает такой же результат для процента угаданных знаков, что и взвешенное мнение 25 экспертов.
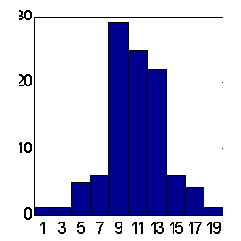
Рис. 8.14.  Гистограмма сумм угаданных знаков при средних предсказаниях 25 экспертов. Среднее по 100 комитетам = 11.7 при стандартном отклонении 3.2


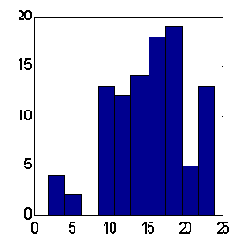
Рис. 8.15.  Гистограмма сумм угаданных знаков при взвешенных предсказаниях тех же 25 экспертов. Среднее по 100 комитетам = 15.2 при стандартном отклонении 4.9

Измерение качества предсказаний

Хотя предсказание финансовых рядов и сводится к задаче аппроксимации многомерной функции, оно имеет свои особенности как при формировании входов, так и при выборе выходов нейросети. Первый аспект, касающийся входов, мы уже обсудили. Теперь коснемся особенностей выбора выходных переменных. Но прежде ответим на главный вопрос: как измерить качество финансовых предсказаний. Это поможет определить наилучшую стратегию обучения нейросети.

Эмпирические свидетельства предсказуемости финансовых рядов

Метод погружения позволяет количественно измерить предсказуемость реальных финансовых инструментов, т.е. проверить или опровергнуть гипотезу эффективности рынка. Согласно последней, разброс точек по всем координатам лагового пространства одинаков (если они - одинаково распределенные независимые случайные величины). Напротив, хаотическая динамика, обеспечивающая определенную предсказуемость, должна приводить к тому, что наблюдения будут группироваться вблизи некоторой гиперповерхности

, т.е. экспериментальная выборка формирует некоторое множество размерности меньшей, чем размерность всего лагового пространства.

Для измерения размерности можно воспользоваться следующим интуитивно понятным свойством: если множество имеет размерность

, то при разбиении его на все более мелкие покрытия кубиками со стороной , число таких кубиков растет как . На этом факте основывается определение размерности множеств уже знакомым нам методом box-counting. Размерность множества точек определяется по скорости возрастания числа ячеек (boxes), содержащих все точки

множества. 1)

Для ускорения алгоритма размеры

берут кратными 2, т.е. масштаб разрешения измеряется в битах.

В качестве примера типичного рыночного временного ряда возьмем такой известный финансовый инструмент, как индекс котировок акций 500 крупнейших компаний США, S&P500, отражающий среднюю динамику цен на Нью-Йоркской бирже. рисунок 8.3 показывает динамику индекса на протяжении 679 месяцев. Размерность (информационная) приращений этого ряда, подсчитанная методом box-counting, показана на следующем рисунке ( рисунок 8.4).

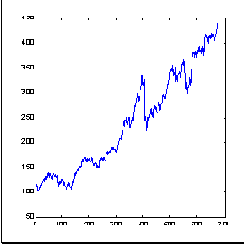
Рис. 8.3.  Временной ряд 679 значений индекса S&P500, используемый на протяжении данной лекции в качестве примера

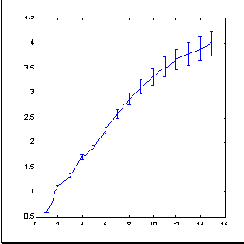
Рис. 8.4.  Информационая размерность приращений ряда S&P500

Как следует из последнего рисунка, в 15-мерном пространстве погружения экспериментальные точки формируют множество размерности примерно 4. Это значительно меньше, чем 15, что мы получили бы исходя из гипотезы эффективного рынка, считающей ряд приращений независимыми случайными величинами.

Таким образом, эмпирические данные убедительно свидетельствуют о наличии некоторой предсказуемой составляющей в финансовых временных рядах, хотя здесь и нельзя говорить о полностью детерминированной хаотической

динамике. 2)

Значит попытки применения нейросетевого анализа для предсказания рынков имеют под собой веские основания.

Заметим, однако, что теоретическая предсказуемость вовсе не гарантирует достижимость практически значимого уровня предсказаний. Количественную оценку предсказуемости конкретных рядов дает измерение кросс-энтропии, также возможное с помощью методики box-counting. Для примера приведем измерения предсказуемости приращений индекса S&P500 в зависимости от глубины

погружения. 3)Кросс-энтропия , график которой приведен ниже ( рисунок 8.5), измеряет дополнительную информацию о следующем значении ряда, обеспеченную знанием прошлых значений этого ряда.
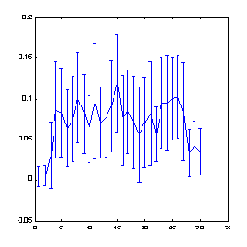
Рис. 8.5.  Предсказуемость знака приращений ряда индекса S&P500 в зависимости от глубины погружения (ширины "окна"). Увеличение глубины погружения свыше 25 сопровождается снижением предсказуемости

Далее в этой лекции мы оценим какой доход в принципе способен обеспечить такой уровень предсказуемости.



Таким образом, эмпирические данные убедительно свидетельствуют о наличии некоторой предсказуемой составляющей в финансовых временных рядах, хотя здесь и нельзя говорить о полностью детерминированной хаотической

динамике. 3)

Значит попытки применения нейросетевого анализа для предсказания рынков имеют под собой веские основания.

Заметим, однако, что теоретическая предсказуемость вовсе не гарантирует достижимость практически значимого уровня предсказаний. Количественную оценку предсказуемости конкретных рядов дает измерение кросс-энтропии, также возможное с помощью методики box-counting. Для примера приведем измерения предсказуемости приращений индекса S&P500 в зависимости от глубины

погружения. 4)Кросс-энтропия , график которой приведен ниже ( рисунок 8.5), измеряет дополнительную информацию о следующем значении ряда, обеспеченную знанием прошлых значений этого ряда.
Рис. 8.5.  Предсказуемость знака приращений ряда индекса S&P500 в зависимости от глубины погружения (ширины "окна"). Увеличение глубины погружения свыше 25 сопровождается снижением предсказуемости

Далее в этой лекции мы оценим какой доход в принципе способен обеспечить такой уровень предсказуемости.

Кому нужно предсказывать рынок?

Предсказание финансовых временных рядов - необходимый элемент любой инвестиционной деятельности. Сама идея инвестиций - вложения денег сейчас с целью получения дохода в будущем - основывается на идее прогнозирования будущего. Соответственно, предсказание финансовых временных рядов лежит в основе деятельности всей индустрии инвестиций - всех бирж и небиржевых систем торговли ценными бумагами.

Приведем несколько цифр, иллюстрирующих масштаб этой индустрии предсказаний (Шарп, 1997). Дневной оборот рынка акций только в США превышает $10 млрд. Депозитарий DTC (Depositary Trust Company) в США, где зарегистрировано ценных бумаг на сумму $11 трлн (из общего объема $18 трлн), регистрирует в день сделок примерно на $250 млрд. Еще более активно идет торговля на мировом валютном рынке FOREX. Его дневной оборот превышает $1000 млрд. Это примерно 1/50 всего совокупного капитала человечества.

Известно, что 99% всех сделок - спекулятивные, т.е. направлены не на обслуживание реального товарооборота, а заключены с целью извлечения прибыли по схеме "купил дешевле - продал дороже". Все они основаны на предсказаниях изменения курса участниками сделки. Причем, что немаловажно, предсказания участников каждой сделки противоположны друг

другу 1)

Так что объем спекулятивных операций характеризует степень различий в предсказаниях участников рынка, т.е реально - степень непредсказуемости финансовых временных рядов.

Метод искусственных примеров (hints)

Одним из самых "больных мест" в финансовых предсказаниях является дефицит примеров для обучения нейросети. Финансовые рынки, вообще говоря, не стационарны (особенно российские). Появляются новые финансовые инструменты, для которых еще не накоплена история, изменяется характер торговли на прежних рынках. В этих условиях длина доступных для обучения нейросети временных рядов весьма ограничена.

Однако, можно повысить число примеров, используя для этого те или иные априорные соображения об инвариантах динамики временного ряда. Это еще одно физико-математическое понятие, способное значительно улучшить качество финансовых предсказаний. Речь идет о генерации искусственных примеров, получаемых из уже имеющихся применением к ним различного рода преобразований.

Поясним основную мысль на примере. Психологически оправдано следующее предположение: игроки обращают внимание, в основном, на форму кривой цен, а не на конкретные значения по осям. Поэтому если немного растянуть по оси котировок весь временной ряд, то полученный в результате такого преобразования ряд также можно использовать для обучения наряду с исходным. Мы, таким образом, удвоили число примеров за счет использования априорной информации, вытекающей из психологических особенностей восприятия временных рядов участниками

рынка. 1)

Более того, мы не просто увеличили число примеров, но и ограничили класс функций, среди которых ищется решение, что также повышает качество предсказаний (если, конечно, использованный инвариант соответствует действительности).

Приведенные ниже результаты вычисления предсказуемости индекса S&P500 методом box-counting (см. рисунки 8.7, 8.8) иллюстрируют роль искусственных примеров. Пространство признаков в данном случае формировалось методом ортогонализации, описанным в лекции о способах предобработки данных. В качестве входных переменных использовались 30 главных компонент в 100-мерном лаговом пространстве. Из этих главных компонент были выбраны 7 признаков - наиболее значимые ортогональные линейные комбинации.
Как видно из этих рисунков, лишь применение искусственных примеров оказалось способным в данном случае обеспечить заметную предсказуемость.

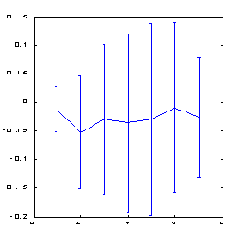
Рис. 8.7.  Предсказуемость знака изменения котировок индекса S&P500


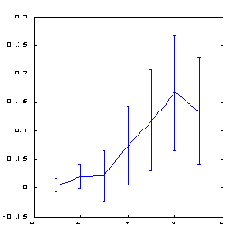
Рис. 8.8.  Предсказуемость знака изменения котировок индекса S&P500 после учетверения числа примеров методом растяжения по оси цен

Обратите внимание, что использование ортогонального пространства признаков привело к некоторому повышению предсказуемости по сравнению с обычным способом погружения: с 0.12 бит ( рисунок 8.5) до 0.17 бит (рисунок 8.8). Чуть позже, когда пойдет речь о влиянии предсказуемости на прибыль, мы покажем, что за счет этого норма прибыли может увеличиться почти в полтора раза.

Другой, менее тривиальный, пример удачного использования такого рода подсказок (hints) для нейросети в каком направлении искать решение - использование скрытой симметрии в валютной торговле. Смысл этой симметрии в том, что валютные котировки могут рассмматриваться с двух "точек зрения", например как ряд DM/$ или как ряд $/DM. Возрастание одного из них соответствует уменьшению другого. Это свойство можно использовать для удвоения числа примеров: каждому примеру вида можно добавить его симметричный аналог . Эксперименты по нейросетевому предсказанию показали, что для основных валютных рынков учет симметрии поднимает норму прибыли примерно в два раза, конкретно - с 5% годовых до 10% годовых, с учетом реальных транзакционных издержек (Abu-Mostafa, 1995).

Метод погружения. Теорема Такенса

Начнем с этапа погружения. Как мы сейчас убедимся, несмотря на то, что предсказания, казалось бы, являются экстраполяцией данных, нейросети, на самом деле, решают задачу интерполяции, что существенно повышает надежность решения. Предсказание временного ряда сводится к типовой задаче нейроанализа - аппроксимации функции многих переменных по заданному набору примеров - с помощью процедуры погружения ряда в многомерное пространство (Weigend, 1994). Например,

-мерное лаговое пространство ряда состоит из значений ряда в последовательные моменты времени: .

Для динамических систем доказана следующая теорема Такенса. Если временной ряд порождается динамической системой, т.е. значения

есть произвольная функция состояния такой системы, существует такая глубина погружения

(примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда (Sauer, 1991). Таким образом, выбрав достаточно большое можно гарантировать однозначную зависимость будущего значения ряда от его предыдущих значений: , т.е. предсказание временного ряда сводится к задаче интерполяции функции многих переменных. Нейросеть далее можно использовать для восстановления этой неизвестной функции по набору примеров, заданных историей данного временного ряда.

Напротив, для случайного ряда знание прошлого ничего не дает для предсказания будущего. Поэтому, согласно теории эффективного рынка, разброс предсказываемых значений ряда на следующем шаге при погружении в лаговое пространство не изменится.

Отличие хаотической динамики от стохастической (случайной), проявляющееся в процессе погружения, иллюстрирует рисунок 8.2.

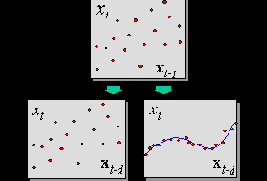
Рис. 8.2.  Проявляющееся по мере погружения ряда различие между случайным процессом и хаотической динамикой

Методика предсказания временных рядов

Для начала обрисуем общую схему нейросетевого предсказания временных рядов (рисунок 8.1).

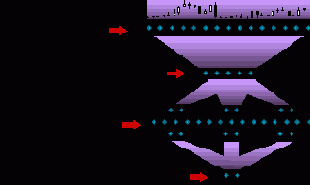
Рис. 8.1.  Схема технологического цикла предсказаний рыночных временных рядов

Далее в этой лекции мы кратко обсудим все этапы этой технологической цепочки. Хотя общие принципы нейро-моделирования применимы к данной задаче в полном объеме, предсказание финансовых временных рядов имеет свою специфику. Именно эти отличительные черты и будут в большей мере затронуты в этой лекции.

Можно ли предсказывать рынок?

Это важнейшее свойство рыночных временных рядов легло в основу теории "эффективного" рынка, изложенной в диссертации Луи де Башелье (L.Bachelier) в 1900 г. Согласно этой доктрине, инвестор может надеяться лишь на среднюю доходность рынка, оцениваемую с помощью индексов, таких как Dow Jones или S&P500 для Нью-Йоркской биржи. Всякий же спекулятивный доход носит случайный характер и подобен азартной игре на деньги. В основе непредсказуемости рыночных кривых лежит та же причина, по которой деньги редко валяются на земле в людных местах: слишком много желающих их поднять.

Теория эффективного рынка не разделяется, вполне естественно, самими участниками рынка (которые как раз и заняты поиском "упавших" денег). Большинство из них уверено, что рыночные временные ряды, несмотря на кажущуюся стохастичность, полны скрытых закономерностей, т.е в принципе хотя бы частично предсказуемы. Такие скрытые эмпирические закономерности пытался выявить в 30-х годах в серии своих статей основатель технического анализа Эллиот (R.Elliott).

В 80-х годах неожиданную поддержку эта точка зрения нашла в незадолго до этого появившейся теории динамического хаоса. Эта теория построена на противопоставлении хаотичности и стохастичности (случайности). Хаотические ряды только выглядят случайными, но, как детерминированный динамический процесс, вполне допускают краткосрочное прогнозирование. Область возможных предсказаний ограничена по времени горизонтом прогнозирования, но этого может оказаться достаточно для получения реального дохода от предсказаний (Chorafas, 1994). И тот, кто обладает лучшими математическими методами извлечения закономерностей из зашумленных хаотических рядов, может надеяться на большую норму прибыли - за счет своих менее оснащенных собратьев.

В этой лекции мы приведем конкретные факты, подтверждающие частичную предсказуемость финансовых временных рядов, и даже оценим эту предсказуемость численно.

Обучение нейросетей

Основная специфика предсказания временных рядов лежит в области предобработки данных. Процедура обучения отдельных нейросетей стандартна. Как всегда, имеющиеся примеры разбиваются на три выборки: обучающая, валидационная и тестовая. Первая используется для обучения, вторая - для выбора оптимальной архитектуры сети и/или для выбора момента остановки обучения. Наконец, третья, которая вообще не использовалась в обучении, служит для контроля качества прогноза обученной нейросети.

Однако, для сильно зашумленных финансовых рядов существенный выигрыш в надежности предсказаний способно дать использование комитетов сетей. Обсуждением этой методики мы и закончим данную лекцию.

В литературе имеются свидетельства улучшения качества предсказаний за счет использования нейросетей с обратными связями. Такие сети могут обладать локальной памятью, сохраняющей информацию о более далеком прошлом, чем то, что в явном виде присутствует во входах. Рассмотрение таких архитектур, однако, увело бы нас слишком далеко от основной темы, тем более, что существуют альтернативные способы эффективного расширения "горизонта" сети, за счет специальных способов погружения ряда, рассмотренных ниже.

Понижение размерности входов: признаки

Подобного рода сжатие информации является примером извлечения из непомерно большого числа входных переменных наиболее значимых для предсказания признаков. Способы систематического извлечения признаков уже были описаны в прошлых лекциях. Их можно (и нужно) с успехом применять и к предсказанию временных рядов.

Важно только, чтобы способ представления входной информации по возможности облегчал процесс извлечения признаков. Вейвлетное представление являет собой пример удачного, с точки зрения извлечения признаков, кодирования (Kaiser, 1995). Например, на следующем рисунке ( рисунок 8.6) изображен отрезок из 50 значений ряда вместе с его реконструкцией по 10 специальным образом отобранным вейвлет-коэффициентов. Обратите внимание, что несмотря на то, что для этого потребовалось в пять раз меньше даных, непосредственное прошлое ряда восстановлено точно, а более далекое - лишь в общих чертах, хотя максимумы и минимумы отражены верно. Следовательно, можно с приемлемой точностью описывать 50-мерное окно всего лишь 10-мерным входным вектором.

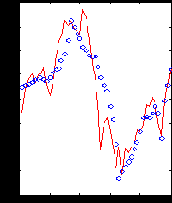
Рис. 8.6.  Пример 50-мерного окна (сплошная линия) и его реконструкции по 10 вейвлет-коэффициентам (о)

Еще один возможный подход - использование в качестве возможных кандидатов в пространство признаков различного рода индикаторов технического анализа, которые автоматически подсчитываются в соответствующих программных пакетах (таких как MetaStock или Windows On Wall Street). Многочисленность этих эмпирических признаков (Colby, 1988) затрудняет пользование ими, тогда как каждый из них может оказаться полезным в применении к данному ряду. Описанные ранее методы позволят отобрать наиболее значимую комбинацию технических индикаторов, которую и следует затем использовать в качестве входов нейросети.

Способы погружения временного ряда

Начнем с того, что в качестве входов и выходов нейросети не следует выбирать сами значения котировок, которые мы обозначим

. Действительно значимыми для предсказаний являются изменения котировок. Поскольку эти изменения, как правило, гораздо меньше по амплитуде, чем сами котировки, между последовательными значениями курсов имеется большая корреляция - наиболее вероятное значение курса в следующий момент равно его предыдущему значению: . Между тем, как это уже неоднократно подчеркивалось, для повышения качества обучения следует стремиться к статистической независимости входов, то есть к отсутствию подобных корреляций.

Поэтому в качестве входных переменных логично выбирать наиболее статистически независимые величины, например, изменения котировок

или логарифм относительного приращения . Последний выбор хорош для длительных временных рядов, когда уже заметно влияние инфляции. В этом случае простые разности в разных частях ряда будут иметь различную амплитуду, т.к. фактически измеряются в различных единицах. Напротив, отношения последовательных котировок не зависят от единиц измерения, и будут одного масштаба несмотря на инфляционное изменение единиц измерения. В итоге, большая стационарность ряда позволит использовать для обучения большую историю и обеспечит лучшее обучение.

Отрицательной чертой погружения в лаговое пространство является ограниченный "кругозор" сети. Технический анализ же, напротив, не фиксирует окно в прошлом, и пользуется подчас весьма далекими значениями ряда. Например, утверждается, что максимальные и минимальные значения ряда даже в относительно далеком прошлом оказывают достаточно сильное воздействие на психологию игроков, и, следовательно, должны быть значимы для предсказания. Недостаточно широкое окно погружения в лаговое пространство не способно предоставить такую информацию, что, естественно, снижает эффективность предсказания. С другой стороны, расширение окна до таких значений, когда захватываются далекие экстремальные значения ряда, повышает размерность сети, что в свою очередь приводит к понижению точности нейросетевого предсказания - уже из-за разрастания размера сети.1)

Выходом из этой, казалось бы, тупиковой ситуации являются альтернативные способы кодирования прошлого поведения ряда. Интуитивно понятно, что чем дальше в прошлое уходит история ряда, тем меньше деталей его поведения влияет на результат предсказаний. Это обосновано психологией субъективного восприятия прошлого участниками торгов, которые, собственно, и формируют будущее. Следовательно, надо найти такое представление динамики ряда, которое имело бы избирательную точность: чем дальше в прошлое - тем меньше деталей, при сохранении общего вида кривой. Весьма перспективным инструментом здесь может оказаться т.н. вейвлетное разложение (wavelet decomposition). Оно эквивалентно по информативности лаговому погружению, но легче допускает такое сжатие информации, которое описывает прошлое с избирательной точностью.

Связь предсказуемости с нормой прибыли

Особенностью предсказния финансовых временных рядов является стремление к получению максимальной прибыли, а не минимизации среднеквадратичного отклонения, как это принято в случае аппроксимации функций.

В простейшем случае ежедневной торговли прибыль зависит от верно угаданого знака изменения котировки. Поэтому нейросеть нужно ориентировать именно на точность угадывания знака, а не самого значения. Найдем как связана норма прибыли с точностью определения знака в простейшей постановке ежедневного вхождения в рынок ( рисунок 8.9).

Рис. 8.9.  Ежедневное вхождение в рынок

Обозначим на момент

: полный капитал игрока , относительное изменение котировки , а в качестве выхода сети возьмем степень ее уверенности в знаке этого изменения . Такая сеть с выходной нелинейностью вида обучается предсказывать знак изменения и выдает прогноз знака с амплитудой пропорциональной его вероятности. Тогда возрастание капитала на шаге запишется в виде:

где

- доля капитала, "в игре". Выигрыш за все время игры:

нам и предстоит максимизировать, выбрав оптимальный размер ставок

. Пусть в среднем игрок угадывает долю знаков и, соответственно, ошибается с вероятностью . Тогда логарифм нормы прибыли,

а следовательно и сама прибыль, будет максимальным при значении

и составит в среднем:

Здесь мы ввели коэффициент

. Например, для Гауссова распределения . Степень предсказуемости знака напрямую связана с кросс-энтропией, которую можно оценить a priory методом box-counting. Для бинарного выхода (см. рисунок 8.10):

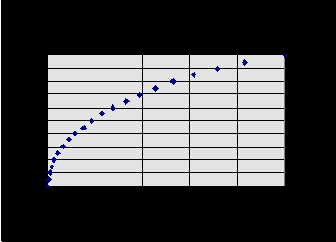
Рис. 8.10.  Доля правильно угаданных направлений изменений ряда как функция кросс-энтропии знака выхода при известных входах

В итоге получаем следующую оценку нормы прибыли при заданной величине предсказуемости знака

, выраженной в битах:

То есть, для ряда с предсказуемостью

в принципе возможно удвоить капитал за вхождений в рынок. Так, например, измеренная выше предсказуемость временного ряда S&P500, равная (см.
рисунок 8.8) предполагает удвоение капитала в среднем за вхождений в рынок. Таким образом, даже небольшая предсказуемость знака изменения котировок способна обеспечить весьма заметную норму прибыли.

Подчеркнем, что оптимальная норма прибыли требует достаточно аккуратной игры, когда при каждом вхождении в рынок игрок рискует строго определенной долей капитала:

где - типичная при данной волатильности рынка величина выигрыша или

проигрыша. 1) Как меньшие, так и большие значения ставок уменьшают прибыль. Причем, чересчур рискованная игра может привести к проигрышу при любой предсказательной способности. Этот факт иллюстрирует рисунок 8.11.


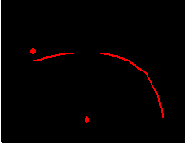
Рис. 8.11.  Зависимость средней нормы прибыли от выбора доли капитала "на кону"

Поэтому приведенные выше оценки дают представление лишь о верхнем пределе нормы

прибыли. 2)

Более тщательный анализ с учетом влияния флуктуаций, выходит за рамки нашего изложения. Качественно понятно, однако, что выбор оптимального размера контрактов требует оценки точности предсказаний на каждом шаге.

Технический анализ и нейронные сети

В последнее десятилетие наблюдается устойчивый рост популярности технического анализа - набора эмпирических правил, основанных на различного рода индикаторах поведения рынка. Технический анализ сосредотачивается на индивидуальном поведении данного финансового инструмента, вне его связи с остальными ценными бумагами (Pring, 1991).

Такой подход психологически обоснован сосредоточенностью брокеров именно на том инструменте, с которым они в данный момент работают. Согласно Александру Элдеру (A.Elder), известному специалисту по техническому анализу (по своей предыдущей специальности - психотерапевту), поведение рыночного сообщества имеет много аналогий с поведением толпы, характеризующимся особыми законами массовой психологии. Влияние толпы упрощает мышление, нивелирует индивидуальные особенности и рождает формы коллективного, стадного поведения, более примитивного, чем индивидуальное. В частности, стадные инстинкты повышают роль лидера, вожака. Ценовая кривая, по Элдеру, как раз и является таким лидером, фокусируя на себе коллективное сознание рынка. Такая психологическая трактовка поведения рыночной цены обосновывает применение теории динамического хаоса. Частичная предсказуемость рынка обусловлена относительно примитивным коллективным поведением игроков, которые образуют единую хаотическую динамическую систему с относительно небольшим числом внутренних степеней свободы.

Согласно этой доктрине, для предсказания рыночных кривых необходимо освободиться от власти толпы, стать выше и умнее ее. Для этого предлагается выработать систему игры, апробированную на прошлом поведении временного ряда и четко следовать этой системе, не поддаваясь влиянию эмоций и циркулирующих вокруг данного рынка слухов. Иными словами, предсказания должны быть основаны на алгоритме, т.е. их можно и даже должно перепоручить компьютеру (LeBeau, 1992). За человеком остается лишь создание этого алгоритма, для чего в его распоряжении имеются многочисленные программные продукты, облегчающие разработку и дальнейшее сопровождение компьютерных стратегий на базе инструментария технического анализа.

Следуя этой логике, почему бы не использовать компьютер и на этапе разработки стратегии, причем не в качестве ассистента, рассчитывающего известные рыночные индикаторы и тестирующего заданные стратегии, а для извлечения оптимальных индикаторов и нахождения оптимальных стратегий по найденным индикаторам. Такой подход - с привлечением технологии нейронных сетей - завоевывает с начала 90-х годов все больше приверженцев (Beltratti, 1995, Бэстенс, 1997), т.к. обладает рядом неоспоримых достоинств.

Во-первых, нейросетевой анализ, в отличие от технического, не предполагает никаких ограничений на характер входной информации. Это могут быть как индикаторы данного временного ряда, так и сведения о поведении других рыночных инструментов. Недаром нейросети активно используют именно институциональные инвесторы (например, крупные пенсионные фонды), работающие с большими портфелями, для которых особенно важны корреляции между различными рынками.

Во-вторых, в отличие от теханализа, основанного на общих рекомендациях, нейросети способны находить оптимальные для данного инструмента индикаторы и строить по ним оптимальную опять же для данного ряда стратегию предсказания. Более того, эти стратегии могут быть адаптивны, меняясь вместе с рынком, что особенно важно для молодых активно развивающихся рынков, в частности, российского.

Нейросетевое моделирование в чистом виде базируется лишь на данных, не привлекая никаких априорных соображений. В этом его сила и одновременно - его ахиллесова пята. Имеющихся данных может не хватить для обучения, размерность потенциальных входов может оказаться слишком велика. Далее в этой лекции мы покажем как для преодоления этих типичных в области финансовых предсказаний трудностей можно воспользоваться опытом, накопленным техническим анализом.

Возможная норма прибыли нейросетевых предсказаний

До сих пор результаты численных экспериментов формулировались нами в виде процента угаданных знаков. Зададимся теперь вопросом о реально достижимой норме прибыли при игре с помощью нейросетей. Полученные выше без учета влияния флуктуаций верхние границы нормы прибыли вряд ли достижимы на практике, тем более, что до сих пор мы не учитывали транзакционных издержек, которые могут свести на нет достигнутую степень предсказуемости.

Действительно, учет комиссионных приводит к появлению отрицательного члена в показателе экспоненты:

Причем, в отличае от степени предсказуемости

, комиссия входит не квадратично, а линейно. Так, в приведенном выше примере типичные значения предсказуемости не смогут "пересилить" комиссию свыше .

Чтобы дать читателю представление о реальных возможностях нейросей в этой области, приведем результаты автоматического неросетевого трейдинга на трех финансовых инструментах, с различными характерными временами: значения индекса S$P500 с месячными интервалами между отсчетами, дневные котировки немецкой марки DM/$ и часовые отсчеты фьючерсов на акции Лукойл на Российской бирже. Статистика предсказаний набиралась на 50 различных нейросистемах (содержащих комитеты из 50 нейросетей каждая). Сами ряды и результаты по предсказанию знаков на тестовой выборке из 100 последних значений каждого ряда приведены на следующем рисунке.

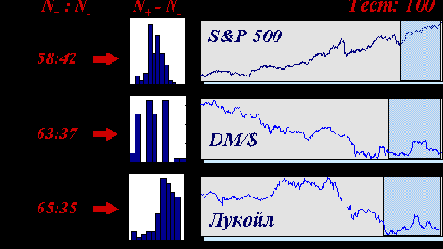
Рис. 8.16. 

Эти результаты подтверждают интуитивно понятную закономерность: ряды тем более предсказуемы, чем меньше времени проходит между его отсчетами. Действительно, чем больше временной масштаб между последовательными значениями ряда, тем больше внешней по отношению к его динамике информации доступно участникам рынка, и, соответственно меньше информации о будущем содержится в самом ряде.

Далее полученные выше предсказания использовались для игры на тестовой выборке. При этом, размер контракта на каждом шаге выбирался пропорциональным степени уверенности предсказания, а значение глобального параметра

оптимизировалось по обучающей выборке.
Кроме того, в зависимости от своих успехов, каждая сеть в комитете имела свой плавающий рейтинг, и в предсказаниях на каждом шаге использовалась лишь "лучшая" в данный момент половина сетей. Результаты таких нейро-трейдеров показаны на следующем рисунке (рисунок 8.17).
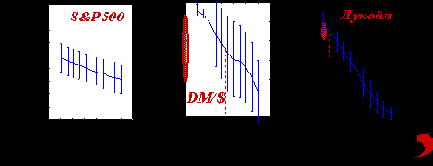
Рис. 8.17.  Статистика выигрышей по 50 реализациям в зависимости от величины комиссионных. Реалистичные значения комиссионных, показанные пунктиром, определяют область реально достижимых норм прибыли


Итоговый выигрыш (как и сама стратегия игры), естественно, зависит от величины комиссионных. Эта зависимость и изображена приведенных выше графиках. Там, где реалистичные значения комиссионных в выбранных единицах измерений были известны авторам, они отмечены на рисунке. Уточним, что в этих экспериментах не учитывалась "квантованность" реальной игры, т.е. то, что величина сделок должна равняться целому числу типовых контрактов. Этот случай соответствует игре на большом капитале, когда типичные сделки содержат много контрактов. Кроме того, подразумевалась залоговая форма игры, т.е. норма прибыли исчислялась к залоговому капиталу, гораздо меньшему, чем масштабы самих контрактов.

Приведенные выше результаты свидетельствуют о перспективности нейросетевого трейдинга, по крайней мере на "коротких" временных масштабах. Более того, в силу самоподобия финансовых временных рядов (Peters, 1994), норма прибыли за единицу времени будет тем выше, чем меньше характерное время трейдинга. Таким образом, автоматические нейросетевые трейдеры оказываются наиболее эффективны при торговле в реальном времени, где как раз наиболее заметны их преимущества над обычными брокерами: неутомляемость, неподверженность эмоциям, потенциально гораздо более высокая скорость реагирования. Обученная нейросеть, подсоединенная к электронной системе торгов, может принимать решения еще до того, как брокер-человек успеет распознать изменения графика котировок на своем терминале.



Кроме того, в зависимости от своих успехов, каждая сеть в комитете имела свой плавающий рейтинг, и в предсказаниях на каждом шаге использовалась лишь "лучшая" в данный момент половина сетей. Результаты таких нейро-трейдеров показаны на следующем рисунке (рисунок 8.17).
Рис. 8.17.  Статистика выигрышей по 50 реализациям в зависимости от величины комиссионных. Реалистичные значения комиссионных, показанные пунктиром, определяют область реально достижимых норм прибыли


Итоговый выигрыш (как и сама стратегия игры), естественно, зависит от величины комиссионных. Эта зависимость и изображена приведенных выше графиках. Там, где реалистичные значения комиссионных в выбранных единицах измерений были известны авторам, они отмечены на рисунке. Уточним, что в этих экспериментах не учитывалась "квантованность" реальной игры, т.е. то, что величина сделок должна равняться целому числу типовых контрактов. Этот случай соответствует игре на большом капитале, когда типичные сделки содержат много контрактов. Кроме того, подразумевалась залоговая форма игры, т.е. норма прибыли исчислялась к залоговому капиталу, гораздо меньшему, чем масштабы самих контрактов.

Приведенные выше результаты свидетельствуют о перспективности нейросетевого трейдинга, по крайней мере на "коротких" временных масштабах. Более того, в силу самоподобия финансовых временных рядов (Peters, 1994), норма прибыли за единицу времени будет тем выше, чем меньше характерное время трейдинга. Таким образом, автоматические нейросетевые трейдеры оказываются наиболее эффективны при торговле в реальном времени, где как раз наиболее заметны их преимущества над обычными брокерами: неутомляемость, неподверженность эмоциям, потенциально гораздо более высокая скорость реагирования. Обученная нейросеть, подсоединенная к электронной системе торгов, может принимать решения еще до того, как брокер-человек успеет распознать изменения графика котировок на своем терминале.

Предсказание как вид бизнеса

В этой лекции рассмотрено одно из самых популярных практических приложений нейросетей - предсказание рыночных временных рядов. В этой области предсказания наиболее тесно связаны с доходностью, и могут рассматриваться как один из видов бизнеса.

Выбор функционала ошибки

Для обучения нейросети недостаточно сформировать обучающие наборы входов-выходов. Необходимо также определить ошибку предсказаний сети. Среднеквадратичная ошибка, используемая по умолчанию в большинстве нейросетевых приложений, не имеет большого "финансового смысла" для рыночных рядов. Поэтому в отдельном разделе мы рассмотрим специфичные для финансовых временных рядов функции ошибки и покажем их связь с возможной нормой прибыли.

Например, для выбора рыночной позиции надежное определение знака изменения курса более важно, чем понижение среднеквадратичного отклонения. Хотя эти показатели и связаны между собой, сети оптимизированные по одному из них будут давать худшие предсказания другого. Выбор адекватной функции ошибки, как мы покажем далее в этой лекции, должен опираться на некую идеальную стратегию и диктоваться, например, максимизацией прибыли (или минимизацией возможных убытков).

Для обучения нейросети недостаточно сформировать обучающие наборы входов-выходов. Необходимо также определить ошибку предсказаний сети. Среднеквадратичная ошибка, используемая по умолчанию в большинстве нейросетевых приложений, не имеет большого "финансового смысла" для рыночных рядов. Поэтому в отдельном разделе мы рассмотрим специфичные для финансовых временных рядов функции ошибки и покажем их связь с возможной нормой прибыли.

Например, для выбора рыночной позиции надежное определение знака изменения курса более важно, чем понижение среднеквадратичного отклонения. Хотя эти показатели и связаны между собой, сети оптимизированные по одному из них будут давать худшие предсказания другого. Выбор адекватной функции ошибки, как мы покажем далее в этой лекции, должен опираться на некую идеальную стратегию и диктоваться, например, максимизацией прибыли (или минимизацией возможных убытков).

Если принять, что целью предсказаний финансовых временных рядов является максимизация прибыли, логично настраивать нейросеть именно на этот конечный результат. Например, при игре по описанной выше схеме для обучения нейросети можно выбрать следующую функцию ошибки обучения, усредненную по всем примерам из обучающей выборки:

Здесь доля капитала в игре введена в качестве дополнительного выхода сети, настраиваемого в процессе обучения. При таком подходе, первый нейрон,

, с функцией активации даст вероятность возрастания или убывания курса, в то время как второй выход сети даст рекомендованную долю капитала в игре на данном шаге.

Поскольку, однако, в соответствии с предыдущим анализом, эта доля должна быть пропорциональна степени уверености предсказания, можно заменить два выхода сети - одним, положив

, и ограничиться оптимизацией всего одного глобального параметра минимизирующего ошибку:

Тем самым, появляется возможность регулировать ставку в соответствии с уровнем риска, предсказываемым сетью. Игра с переменными ставками приносит большую прибыль, чем игра с фиксированными ставками. Действительно, если зафиксировать ставку, определив ее по средней предсказуемости, то скорость роста капитала будет пропорциональна

, тогда как если определять оптимальную ставку на каждом шаге, то - пропорциональна .

по крайней мере некоторые) рыночные

Подытожим результаты этой лекции. Во-первых, мы показали, что ( по крайней мере некоторые) рыночные временные ряды частично предсказуемы. Как и любой другой вид нейроанализа, предсказание временных рядов требует достаточно сложной и тщательной предобработки данных. Однако, работа с временными рядами имеет свою специфику, которую можно использовать для увеличения прибыли. Это касается как выбора входов (использование специальных способов представления данных), так и выбора выходов и использования специфических функционалов ошибки. Наконец, мы показали, насколько выгоднее может быть использование комитетов нейро-экспертов по сравнению с отдельными нейросетями, и представили данные о реальных нормах прибыли на нескольких реальных финансовых инструментах.

Исправление данных

Итак, перед извлечением правил из нейронной сети производится ее обучение и прореживание. Упомянем еще об одной процедуре, которая иногда осуществляется при извлечении знаний из нейронных сетей - исправление (очищении). Подобная операция была предложена Вайгендом и коллегами и по сути используется параллельно с обучением (Weigend, Zimmermann, & Neuneier 1996). Гибридное использование обучения и исправления данных носит название CLEARNING (CLEARING+LEARNING). Данная процедура включает восходящий процесс обучения, при котором данные изменяют связи в нейронной сети и нисходящий процесс, в котором нейронная сеть изменяет данные, на которых производится обучение. Ее достоинствами являются выявление и удаление информационных записей, выпадающих из общей структуры обучающей выборки, а также замена искаженных данных и данных с лакунами на исправленные величины. При использовании данной процедуры происходит торг между доверием к данным и доверием к нейросетевой модели, обучаемой на этих данных. Эта конкур енция составляет существо так называемой дилеммы наблюдателя и наблюдений.

2Способность работать с неточными данными является одним из главных достоинств нейронных сетей. Но она же парадоксальным образом является и их недостатком. Действительно, если данные не точны, то сеть в силу своей гибкости и адаптируемости будет подстраиваться к ним, ухудшая свои свойства обобщения. Эта ситуация особенно важна при работе с финансовыми данными. В последнем случае существует множество источников погрешности. Это и ошибки при вводе числовых значений или неправильная оценка времени действия ценных бумаг (например, они уже не продаются). Кроме того, если даже данные и введены правильно, они могут быть слабыми индикаторами основополагающих экономических процессов, таких как промышленное производство или занятость. Наконец, возможно, что многие важные параметры не учитываются при обучении сети, что эффективно может рассматриваться как введение дополнительного шума. Данные, далеко выпадающие из общей тенденции, забирают ресурсы нейронной сети.
Некоторые из нейронов скрытого слоя могут настраива ться на них. При этом ресурсов для описания регулярных слабо зашумленных областей может и не хватить. Множество попыток применения нейронных сетей к решению финансовых задач выявило важное обстоятельство: контроль гибкости нейросетевой модели является центральной проблемой. Изложим кратко существо процедуры обучения сети, объединенной с исправлением данных. Для простоты рассмотрим сеть с одним входом и одним выходом. В этом случае минимизируемой величиной является сумма двух слагаемых (Weigend & Zimmermann, 1996):

Первый член описывает обычно минимизируемое в методе обратного распространения ошибки квадратичное отклонение выхода нейронной сети от желаемого значения . Второе слагаемое представляет собой квадратичное отклонение исправленного входного значения от реального его значения . Соответственно, для весов сети и для исправленных входных значений получаются два правила их модификации. Для весов оно такое же, как и в стандартном методе обратного распространения ошибки, а для исправленного входа имеет вид

где индекс определяет номер итерации данного входа. Представляя в виде суммы подлинного начального входного значения и поправки , получим для последней следующее уравнение итерационного изменения



Это уравнение включает

экспоненциальное затухание : в отсутствие нового входа стремится к нулю со скоростью пропорциональной . член, пропорциональный ошибке выходного значения : аналогичная пропорциональность свойственна и обычному соотношению для модификации весов - чем больше ошибка, тем больше ее влияние на исправление входного значения. Этот член также пропорционален чувствительности выхода ко входу - .

3Вайгенд и его коллеги предложили наглядную механическую интерпретацию минимизируемой функции, а также отношению скоростей обучения и исправления (см. рисунок 9.4).


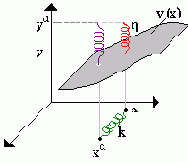
Рис. 9.4.  Механическая аналогия конкуренции между обучением и исправлением данных. К реальному входу присоединяется пружина и растягивается другим концом до точки , что сопровождается увеличением энергии в пружине на .


Но при этом энергия, запасенная в пружине, связывающей реальное и желаемое значения выхода сети, может уменьшиться (растяжение правой пружины меньше, чем левой) так, что суммарная энергия двух пружин уменьшается

При обычном обучении (без исправления входного вектора) данные располагаются в пространстве вход-выход. Наблюдаемое выходное значение состояния выходного нейрона может рассматриваться как поверхность над пространством входов. Точки, изображающие данные обучающего набора вертикально прижимаются к этой поверхности пружинами, которые запасают некоторую энергию сжатия. Сложность нейронной сети определяется в конкуренции между жесткостью поверхности и жесткостью пружин. В одном из предельных случаев, бесконечно мягкая сеть (поверхность) пройдет как раз через все точки, определяемые данными. В противоположном случае, чрезмерно эластичные пружины не будут оказывать воздействия на поверхность и менять нейронную сеть.

Введение механизма исправления данных соответствует добавлению пружин в пространстве входов - между каждой точкой данных и исправленным значением . Энергия, запасенная в этих пружинах составляет . Минимизация суммарной функции ошибки соответствует минимизации полной энергии, запасенной в обеих типах пружин. Отношение описывает конкуренцию между важностью ошибок выхода и важностью ошибок входа.

Извлечение правил

Даже если параметры, описывающие признаки классифицируемых объектов, представляют собой непрерывные величины, для их представления можно использовать бинарные нейроны и принцип кодирования типа термометра. При таком способе кодирования область изменения параметра делится на конечное число

интервалов и для представления всех значений, ле-жащих в m-м интервале используется следующее состояние бинарных нейронов: .

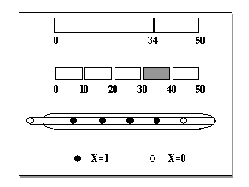
Рис. 9.1.  . Пример кодировки непрерывной величины с помощью бинарных нейронов и принципа термометра. Интервал (0, 50) разбит на 5 равных частей. Значение 34.0 попадает в 4-й интервал. При этом состояния первых 4 из 5 кодирующих бинарных нейронов равно единице, а 5-го - нулю.

При наличии многих непрерывных входов число заменяющих их бинарных нейронов может стать весьма большим. Однако, прореживание связей приводит к получению относительно ком-пактной сети. Но и для нее выделение классификационных правил представляет проблему. Если нейрон имеет d входов, то число различных бинарных векторов, которые он может обра-ботать составляет

, а это большая величина даже при малом d. Далее, состояния нейрона скрытого слоя являются непрерывными, что также является препятствием для извлечения пра-вил. Для его устранения все значения, которые принимают нейроны скрытого слоя кластеризу-ются и заменяются значениями, определяющими центры кластеров. Число таких кластеров выбирается небольшим. После такой дискретизации активностей промежуточных нейронов производится проверка точности классификации объектов сетью. Если она остается приемле-мой, то подготовка к извлечению правил заканчивается. Приведем формальное описание алго-ритма дискретизации значений активности нейронов скрытого слоя

Алгоритм дискретизации

Выбирается значение параметра

, управляющего числом кластеров активности нейрона скрытого слоя. Пусть - активность этого нейрона при предъявлении сети первого вектора обучающего набора. Положим число кластеров , положение кластера . Для всех векторов обучающего набора определяется активность нейрона скрытого слоя если существует индекс такой что

и



то иначе





Заменить на среднее значение активаций нейрона, объединенных в один и тот же кластер: . Проверить точность классификации объектов сетью при замене истинных значений активации нейрона скрытого слоя на . Если точность классификации оказалась ниже заданного значения, то уменьшить значение и вернуться к шагу 1.

Рассмотрим приведенный в (Lu, Setiono and Liu, 1995) пример, в котором прореженная сеть содержала три нейрона скрытого слоя, дискретизация активности которых была проведена при значении параметра . Ее результаты отражены в таблице 9.1.



Таблица 9.1. Дискретизация состояний нейронов скрытого слоя нейрон скрытого слоячисло кластеровдискретное значение активности

1	3	(-1,0,1)
2	2	(0, 1)
3	3	(-1, 0.24, 1)

В этой работе решалась задача разбиения объектов на два класса. На ее примере мы и рассмотрим последовательность извлечения правил. После дискретизации значений активности нейронов скрытого слоя, передача их воздействий выходным классифицирующим нейронам описывалась параметрами, приведенными в таблице 9.2.



Таблица 9.2. Связь дискретных значений активности нейронов скрытого и выходного слоев. h1h2h3o1o2

-1	1	-1	0.92	0.08
-1	1	1	0.00	1.00
-1	1	0.24	0.01	0.99
-1	0	-1	1.00	0.00
-1	0	1	0.11	0.89
-1	0	0.24	0.93	0.07
1	1	-1	0.00	1.00
1	1	1	0.00	1.00
1	1	0.24	0.00	1.00
1	0	-1	0.89	0.11
1	0	1	0.00	1.00
1	0	0.24	0.00	1.00
0	1	-1	0.18	0.82
0	1	1	0.00	1.00
0	1	0.24	0.00	1.00
0	0	-1	1.00	0.00
0	0	1	0.00	1.00
0	0	0.24	0.18	0.82

Исходя из значений, приведенных в этой таблице, после замены значений выходных нейронов ближайшими к ним нулями или единицами, легко получить следующие правила, связывающие активности нейронов скрытого слоя с активностями классифицирующих нейронов

правило 1 если h2=0,h3=-1, то o1=1, o2=0 (объект класса А) правило 2 если h1=-1,h2=1,h3=-1, то o1=1, o2=0 (объект класса А) правило 3 если h1=-1,h2=0,h3=0.24, то o1=1, o2=0 (объект класса А) правило 4 в остальных случаях o1=1, o2=0 (объект класса В)

Эти правила являются вспомогательными, поскольку нам необходимо связать значения состояний классифицирующих выходных нейронов со входами нейронной сети. Структура данной сети после прореживания связей и нейронов изображена на следующем рисунке.




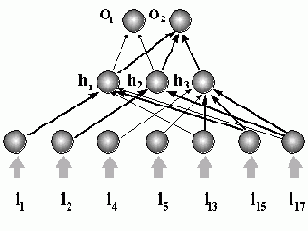
Рис. 9.2.  Двухслойная сеть после прореживания связей и входных нейронов. Положительные связи выделены.

Связь между активностями входных бинарных нейронов и нейронов скрытого слоя для данной сети определяется следующими правилами:

Для первого нейрона скрытого слоя:




Для второго нейрона скрытого слоя:





Для третьего нейрона скрытого слоя:







Комбинируя эти связи с правилами, связывающими активности нейронов скрытого слоя с ак-тивностями выходных нейронов, получим окончательные классифицирующие правила.









Приведенные выше правила определяют принадлежность объекта первому классу (А). Некото-рые из них могут оказаться нереализуемыми, если учесть, что состояния бинарных нейронов кодируют соответствующие непрерывные величины с помощью принципа термометра.

Количество правил, полученных в данном случае, невелико. Однако, иногда даже после проце-дуры прореживания некоторые нейроны скрытого слоя могут иметь слишком много связей с входными нейронами. В этом случае извлечение правил становится нетривиальным, а если оно и осуществлено, то полученные правила не так просто понять. Для выхода из этой ситуации для каждого из "проблемных" нейронов скрытого слоя можно использовать вспомогательные двух-слойные нейронные сети. Во вспомогательной сети количество выходных нейронов равно чис-лу дискретных значений соответствующего "проблемного" нейрона скрытого слоя, а входными нейронами являются те, которые в исходной прореженной сети связаны с данным нейроном скрытого слоя.


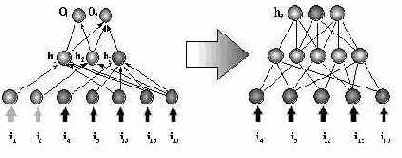
Рис. 9.3.  . Третий нейрон скрытого слоя связан с максимальным числом входов. Число дискретных значений его активности равно 3. Для облегчения процедуры выделения классифицирующих правил этот нейрон может быть заменен вспомогательной сетью с тремя выходными нейронами, кодирующими дискретные значения активности.

Обучающие примеры для вспомогательной сети группируются согласно их дискретизованным значениям активации "проблемного" нейрона.


Для дискретных значений всем обучающим примерам, соответствующим уровню активации , ставится в соответствие -мерный целевой вектор, состоящий из нулей и одной единицы в -й позиции. Вспомогательная сеть содержит свой слой скрытых нейронов. Она обучается и прореживается тем же способом, что и основная нейронная сеть. Метод извлечения правил применяется к каждой вспомогатель-ной сети, для того чтобы связать значения входов с дискретными значениями активации про-блемных нейронов скрытого слоя оригинальной сети. Подобный процесс осуществляется ре-курсивно для всех скрытых нейронов с большим числом входов до тех пор пока это число не станет достаточно малым или же новая вспомогательная сеть уже не сможет быть далее упро-щена.

Извлечение правил из нейронных сетей

Рассмотрим один из методов извлечения правил из нейронных сетей, обученных решению задачи классификации (Lu, Setiono and Liu, 1995). Этот метод носит название NeuroRule. Задача состоит в классификации некоторого набора данных с помощью многослойного персептрона и последующего анализа полученной сети с целью нахождения классифицирующих правил, описывающих каждый из классов. Пусть A обозначает набор из N свойств A1,A2...AN , а {a} - множество возможных значений, которое может принимать свойство Ai. Обозначим через С множество классов c1,c2...cN. Для обучающей выборки известны ассоциированные пары векторов входных и выходных значений (a1...am,ck), где ck

C. Алгоритм извлечения классифицирующих правил включает три этапа:

Обучение нейронной сети. На этом первом шаге двухслойный персептрон тренируется на обучающем наборе вплоть до получения достаточной точности классификации. Прореживание (pruning) нейронной сети. Обученная нейронная сеть содержит все возможные связи между входными нейронами и нейронами скрытого слоя, а также между последними и выходными нейронами. Полное число этих связей обычно столь велико, что из анализа их значений невозможно извлечь обозримые для пользователя классифицирующие правила. Прореживание заключается в удалении излишних связей и нейронов, не приводящем к увеличению ошибки классификации сетью. Результирующая сеть обычно содержит немного нейронов и связей между ними и ее функционирование поддается исследованию. Извлечение правил. На этом этапе из прореженной нейронной сети извлекаются правила, имеющие форму если (a1

q1) и (a2 q2) и ... и (an qn), то , где - константы, - оператор отношения ( ). Предполагается, что эти правила достаточно очевидны при проверке и легко применяются к большим базам данных.

Рассмотрим все эти шаги более подробно

Извлечение знаний

В последние годы созданы огромные базы данных, в которых хранится информация научного, экономического, делового и политического характера. В качестве примера можно привести GenBank, содержащий террабайты данных о последовательностях ДНК живых организмов. Для работы с подобными базами разработаны компьютерные технологии, позволяющие хранить, сортировать и визуализировать данные, осуществлять быстрый доступ к ним, осуществлять их статистическую обработку. Значительно меньшими являются, однако, достижения в разработке методов и программ, способных обнаружить в данных важную, но скрытую информацию. Можно сказать, что информация находится к данным в таком же отношении, как чистое золото к бедной золотоносной руде. Извлечение этой информации может дать критический толчок в бизнесе, в научных исследованиях и других областях. Подобное нетривиальное извлечение неявной, прежде неизвестной и потенциально полезной информации из больших баз данных и называется Разработкой Данных (Data Mining) или же Открытием Знаний (Knowledge Discovery). Мы будем использовать далее для описания этой области информатики более явный синтетический термин - извлечение знаний. Извлечение знаний использует концепции, разработанные в таких областях как машинное обучение (Machine Learning), технология баз данных (Database Technology), статистика и других.

Главными требованиями, предъявляемыми к методам извлечения знаний, являются эффективность и масштабируемость. Работа с очень большими базами данных требует эффективности алгоритмов, а неточность и, зачастую, неполнота данных порождают дополнительные проблемы для извлечения знаний. Нейронные сети имеют здесь неоспоримое преимущество, поскольку именно они являются наиболее эффективным средством работы с зашумленными данными. Действительно, заполнение пропусков в базах данных - одна из прототипических задач, решаемых нейросетями. Однако, главной претензией к нейронным сетям всегда было отсутствие объяснения. Демонстрация того, что нейронные сети действительно можно использовать для получения наглядно сформулированных правил было важным событием конца 80-х годов.
В 1989 году один из авторов настоящего курса поинтересовался у Роберта Хехт-Нильсена, главы одной из наиболее известных американских нейрокомпьютерных фирм Hecht-Nielsen Neurocomputers, где можно узнать подробности о нейроэкспертных си стемах, информация о которых тогда носила только рекламный характер. Хехт-Нильсен ответил в том смысле, что она не доступна. Но уже через 2-3 месяца после этого в журнале Artificial Intelligence Expert была опубликована информация о том, что после долгих и трудных переговоров Хехт-Нильсен и крупнейший авторитет в области экспертных систем Гэллант запатентовали метод извлечения правил из обученных нейронных сетей и метод автоматической нейросетевой генерации экспертных систем.

Извлечение правил из нейронных сетей подразумевает их предварительное обучение. Поскольку эта процедура требует много времени для больших баз данных, то естественна та критика, которой подвергается использование нейротехнологии для извлечения знаний. Другим поводом для такой критики является трудность инкорпорации в нейронные сети некоторых имеющихся априорных знаний. Тем не менее, главным является артикуляция правил на основе анализа структуры нейронной сети. Если эта задача решается, то низкая ошибка классификации и робастность нейронных сетей дают им преимущества перед другими методами извлечения знаний.

Обучение нейронной сети

Предположим, что обучающий набор данных необходимо расклассифицировать на два класса A и B. В этом случае сеть должна содержать N входных и 2 выходных нейрона. Каждому из классов будут соответствовать следующие активности выходных нейронов (1,0) и (0,1). Подходящее количество нейронов в промежуточном слое, вообще говоря, невозможно определить заранее - слишком большое их число ведет к переобучению, в то время как малое не обеспечивает достаточной точности обучения. Тем не мене, как уже отмечалось ранее, все методы адаптивного поиска числа нейронов в промежуточном слое делятся на два класса, в соответствии с тем, с малого или большого числа промежуточных нейронов стартует алгоритм. В первом случае по мере обучения в сеть добавляются дополнительные нейроны, в противоположном - после обучения происходит уничтожение излишних нейронов и связей. NeuroRule использует последний подход, так что число промежуточных нейронов выбирается достаточно большим. Заметим, что NeuroRule уничтожает также и избыточные входные нейроны, влияние которых на классификацию мало.

В качестве функции активации промежуточных нейронов используется гиперболический тан-генс, так что их состояния изменяются в интервале

. В то же время, функцией активации выходных нейронов является функция Ферми (состояния в интервале ). Обозначим через - состояния выходных нейронов при предъявлении на вход сети вектора признаков -го объекта . Будем считать, что этот объект правильно классифицирован сетью, если

где:

если и если , а . В остальных случаях .

Минимизируемая функция ошибки должна не только направлять процесс обучения в сторону правильной классификации всех объектов обучающей выборки, но и делать малыми значения многих связей в сети, чтобы облегчить процесс их прореживания. Подобную технологию - путем добавления к функции ошибки специально подобранных штрафных членов - мы уже разбирали в лекции 3. В методе NeuroRule функция о шибка включает два слагаемых

где

функция взаимной энтропии, минимизация которой происходит быстрее, чем минимизация среднеквадратичной ошибки.
Штрафная функция

уже фигурировала в лекции 3.

Здесь - число нейронов в скрытом слое, - величина связи, между -м входным и -м скрытым нейронами - вес связи между -м скрытым и -м выходным нейронами.

Использование регуляризирующего члена приводит к дифференциации весов по величи-нам, уменьшая большинство, но сохраняя значения некоторых из них. Обучение сети произво-дится методом обратного распространения ошибки.

Прореживание нейронной сети

Полное число связей в обученной сети составляет

. Можно показать, что связь между входным и промежуточным нейроном можно удалить без снижения точности клас-сификации сетью при выполнении условий и . Аналогичным образом, удаление связи не влияет на качество классификации если .

---

---