Алгоритм Кохонена
В 1982 году финский ученый Тойво Кохонен (Kohonen, 1982) предложил ввести в базовое правило соревновательного обучения информацию о расположении нейронов в выходном слое. Для этого нейроны выходного слоя упорядочиваются, образуя одно- или двумерные решетки. Т.е. теперь положение нейронов в такой решетке маркируется векторным индексом



Функция соседства





В отличае от "газо-подобной" динамике обучения при индивидуальной подстройке прототипов (весов нейронов), обучение по Кохонену напоминает натягивание эластичной сетки прототипов на массив данных из обучающей выборки. По мере обучения эластичность сети постепенно увеличивается, чтобы не мешать окончательной тонкой подстройке весов.
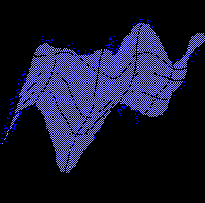
Рис. 4.12. Двумерная топографическая карта набора трехмерных данных. Каждая точка в трехмерном пространстве попадает в свою ячейку сетки имеющую координату ближайшего к ней нейрона из двумерной карты
В результате такого обучения мы получаем не только квантование входов, но и упорядочивание входной информации в виде одно- или двумерной карты. Каждый многомерный вектор имеет свою координату на этой сетке, причем чем ближе координаты двух векторов на карте, тем ближе они и в исходном пространстве. Такая топографическая карта дает наглядное представление о структуре данных в многомерном входном пространстве, геометрию которого мы не в состоянии представить себе иным способом. Визуализация многомерной информации является главным применением карт Кохонена.
Заметим, что в согласии с общим житейским принципом "бесплатных обедов не бывает", топографические карты сохраняют отношение близости лишь локально: близкие на карте области близки и в исходном пространстве, но не наоборот (рисунок 4.13). В общем случае не существует отображения, понижающего размерность и сохраняющего отношения близости глобально.
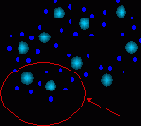
Рис. 4.13. Пример одномерной карты двумерных данных. Стрелкой показана область нарушения непрерывности отображения: близкие на плоскости точки отображаются на противоположные концы карты
Удобным инструментом визуализации данных является раскраска топографических карт, аналогично тому, как это делают на обычных географических картах. Каждый признак данных порождает свою раскраску ячеек карты - по величине среднего значения этого признака у данных, попавших в данную ячейку.

Рис. 4.14. Раскраска топографической карты, индуцированная i-ой компонентой входных данных
Собрав воедино карты всех интересующих нас признаков, получим топографический атлас, дающий интегральное представление о структуре многомерных данных. Далее в этой книге мы рассмотрим практическое применение этой методики к анализу балансовых отчетов и предсказанию банкротств.
Алгоритм обучения соревновательного слоя нейронов
Базовый алгоритм обучения соревновательного слоя остается неизменым:

поскольку задача сети также осталась прежней - как можно точнее отразить входную информацию в выходах сети. Отличае появляется лишь из-за нового способа кодирования выходной информации. В соревновательном слое лишь один нейрон - победитель имеет ненулевой (единичный) выход. Соответственно, в согласии с выписанным выше правилом, лишь его веса корректируются по предъявлении данного примера, причем для победителя правило обучения имеет вид:

Описанный выше базовый алгоритм обучения на практике обычно несколько модифицируют, т.к. он, например, допускает существование т.н. мертвых нейронов, которые никогда не выигрывают, и, следовательно, бесполезны. Самый простой способ избежать их появления - выбирать в качестве начальных значений весов случайно выбранные в обучающей выборке входные вектора.
Такой способ хорош еще и тем, что при достаточно большом числе прототипов он способствует равной "нагрузке" всех нейронов-прототипов. Это соответствует максимизации энтропии выходов в случае соревновательного слоя. В идеале каждый из нейронов соревновательного слоя должен одинаково часто становились победителем, чтобы априори невозможно было бы предсказать какой из них победит при случайном выборе входного вектора из обучающей выборки.
Наиболее быструю сходимость обеспечивает пакетный (batch) режим обучения, когда веса изменяются лишь после предъявления всех примеров. В этом случае можно сделать приращения не малыми, помещая вес нейрона на следующем шаге сразу в центр тяжести всех входных векторов, относящихся к его ячейке. Такой алгоритм сходится за O(1) итераций.
Аппроксиматоры с локальным базисом
Сеть радиального базиса напоминают персептрон с одним скрытым слоем, осуществляя нелинейное отображение




Как тот, так и другой набор базисных функций обеспечивают возможность аппроксимации любой непрерывной функции с произвольной точностью. Основное различие между ними в способе кодирования информации на скрытом слое. Если персепторны используют глобальные переменные (наборы бесконечных гиперплоскостей), то сети радиального базиса опираются на компактные шары, окружающие набор опорных центров (рисунок 4.15).

Рис. 4.15. Глобальная (персептроны) и локальная (сети радиального базиса) методы аппроксимации
В первом случае в аппроксимации в окрестности любой точки участвуют все нейроны скрытого слоя, во втором - лишь ближайшие. Как следствие такой неэффективности, в последнем случае количество опорных функций, необходимых для аппроксимации с заданной точностью, возрастает экспоненциально с размерностью пространства. Это основной недостаток сетей радиального базиса. Основное же их преимущество над персептронами - в простоте обучения.
Автоассоциативные сети
Весьма общим подходом к понижению размерности является использование нелинейных автоассоциативных сетей. В общем случае они должны содержать как минимум три скрытых слоя нейронов. Средний слой - узкое горло, будет в результате обучения выдавать сжатое представление данных . Первый скрытый слой нужен для осуществления произвольного нелинейного кодирования, а последний - для нахождения соответствующего декодера (рисунок 4.8).
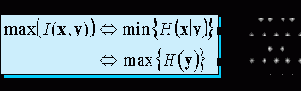
Рис. 4.8. Понижение размерности с помощью автоассоциативных сетей. Минимизация ошибки воспроизведения сетью своих входов эквивалентна оптимальному кодированию в узком горле сети
Задачей автоассоциативных сетей, как уже говорилось, является воспроизведение на выходе сети значений своих входов. Вторая половина сети - декодер - при этом опирается лишь на кодированную информацию в узком горле сети. Качество воспроизведения данных по их кодированному представлению измеряется условной энтропией


Действительно, механическая процедура кодирования не вносит дополнительной неопределенности, так что совместная энтропия входов и их кодового представления равна энтропии самих входов

Привлекательной чертой такого подхода к сжатию информации является его общность. Однако многочисленные локальные минимумы и трудоемкость обучения существенно снижают его практическую ценность.
Более компактные схемы сжатия обеспечивает метод предикторов.
Целевая функция
Наглядной демонстрацией полезности нелинейного анализа главных компонент является следующий простой пример (см. рисунок 4.7).
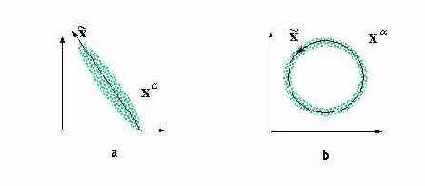
Рис. 4.7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (a). Он не способен, однако, выявить одномерный характер распределения данных в случае (b). Для их одномерной параметризации нужны нелинейные координаты
Он показывает, что в общем случае нас интересует нелинейное преобразование





Гибридное обучение
Относительная автономность базисных функций позволяет разделить обучение на два этапа. На первом этапе обучается первый - соревновательный - слой сети, осуществляя квантование данных. На втором этапе происходит быстрое обучение второго слоя матричными методами, т.к. нахождение коэффициентов второго слоя представляет собой линейную задачу.
Подобная возможность раздельного обучения слоев является основным достоинством сетей радиального базиса. В целом же, области применимости персептронов и сетей радиального базиса коррелируют с найденными выше областями эффективности квантования и понижения размерности (см. рисунок 4.11).
Кластеризация и квантование
Записав правило соревновательного обучения в градиентном виде:


Иными словами, сеть осуществляет кластеризацию данных: находит такие усредненные прототипы, которые минимизируют ошибку огрубления данных. Недостаток такого варианта кластеризации очевиден - "навязывание" количества кластеров, равного числу нейронов. В идеале сеть сама должна находить число кластеров, соответствующее реальной кластеризации векторов в обучающей выборке. Адаптивный подбор числа нейронов осуществляют несколько более сложные алгоритмы, такие, например, как растущий нейронный газ.
Идея последнего подхода состоит в последовательном увеличении числа нейронов-прототипов путем их "деления". Общую ошибку сети можно записать как сумму индивидуальных ошибок каждого нейрона:

Естественно предположить, что наибольшую ошибку будут иметь нейроны, окруженные слишком большим числом примеров и/или имеющие слишком большую ячейку. Такие нейроны и являются, в первую очередь, кандидатами на "почкование" (см. рисунок 4.10).
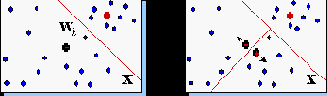
Рис. 4.10. Деление нейрона с максимальной ошибкой в "растущем нейронном газе"
Соревновательные слои нейронов широко используются для квантования данных (vector quantization), отличающегося от кластеризации лишь большим числом прототипов. Это весьма распространенный на практике метод сжатия данных. При достаточно большом числе прототипов, плотность распределения весов соревновательного слоя хорошо аппроксимирует реальную плотность распределения многомерных входных векторов. Входное пространство разбивается на ячейки, содержащие вектора, относящиеся к одному и тому же прототипу. Причем эти ячейки (называемые ячейками Дирихле или ячейками Вороного) содержат примерно одинаковое количество обучающих примеров. Тем самым одновременно минимизируется ошибка огрубления и максимизируется выходная информация - за счет равномерной загрузки нейронов.
Сжатие данных в этом случае достигается за счет того, что каждый прототип можно закодировать меньшим числом бит, чем соответствующие ему вектора данных. При наличии прототипов для идентификации любого из них достаточно лишь

Латеральные связи
Предикторы вводят связи между признаками, обеспечивающие их статистическую независимость. В частном случае линейных предикторов дополнительные сети вырождаются в латеральные связи между нейронами последнего слоя. Эти связи обучаются таким образом, чтобы выходы нейронов этого слоя были некоррелированы.
Между тем, можно предложить и такую схему латеральных связей, которая, наоборот, обеспечивает максимальную коррелированность выходов. Допустим, например, что выход каждого нейрона подается на его вход с положительным весом, а на вход остальных нейронов слоя - с отрицательным. Тем самым, каждый нейрон будет усиливать свой выход и подавлять активность остальных. При логистической функции активации, препятствующей бесконечному росту, победителем в этой борьбе выйдет нейрон с максимальным первоначальным значением выхода. Его значение возрастет до единицы, а активность остальных нейронов затухнет до нуля.
Такие соревновательные слои нейронов также можно использовать для сжатия информации, но это сжатие будет основано на совершенно других принципах.
Нейрон - индикатор
Рассмотрим какие возможности по адаптивной обработке данных имеет единичный нейрон, и как можно сформулировать правила его обучения. В силу локальности нейросетевых алгоритмов, это базовое правило можно будет потом легко распространить и на сети из многих нейронов.
Необходимость взаимодействия нейронов
Если мы просто поместим несколько нейронов в выходной слой и будем обучать каждый из них независимо от других, мы добьемся лишь многократного дублирования одного и того же выхода. Очевидно, что для получения нескольких содержательных признаков на выходе исходное правило обучения должно быть каким-то образом модифицировано - за счет включения взаимодействия между нейронами.
Обобщение данных. Прототипы задач
В этой лекции рассматривается новый тип обучения нейросетей - обучение без учителя (или для краткости - самообучение), когда сеть самостоятельно формирует свои выходы, адаптируясь к поступающим на ее входы сигналам. Как и прежде, такое обучение предполагает минимизацию некоторого целевого функционала. Задание такого функционала формирует цель, в соответствии с которой сеть осуществляет преобразование входной информации.
В отсутствие внешней цели, "учителем" сети могут служить лишь сами данные, т.е. имеющаяся в них информация, закономерности, отличающие входные данные от случайного шума. Лишь такая избыточность позволяет находить более компактное описание данных, что, согласно общему принципу, изложенному в предыдущей лекции, и является обобщением эмпирических данных. Сжатие данных, уменьшение степени их избыточности, использующее существующие в них закономерности, может существенно облегчить последующую работу с данными, выделяя действительно независимые признаки. Поэтому самообучающиеся сети чаще всего используются именно для предобработки "сырых" данных. Практически, адаптивные сети кодируют входную информацию наиболее компактным при заданных ограничениях кодом.
Длина описания данных пропорциональна, во-первых, разрядности данных



Понижение размерности данных с минимальной потерей информации. (Сети, например, способны осуществлять анализ главных компонент данных, выделять наборы независимых признаков.) Уменьшение разнообразия данных за счет выделения конечного набора прототипов, и отнесения данных к одному из таких типов. (Кластеризация данных, квантование непрерывной входной информации.)
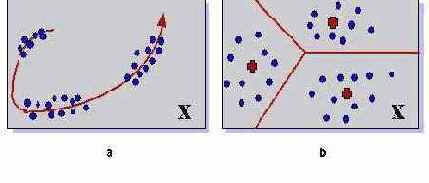
Рис. 4.1. Два типа сжатия информации. Понижение размерности (a) позволяет описывать данные меньшим числом компонент. Кластеризация или квантование (b) позволяет снизить разнообразие данных, уменьшая число бит, требуемых для описания данных
Возможно также объединение обоих типов кодирования. Например, очень богат приложениями метод топографических карт (или самоорганизующихся карт Кохонена - по имени предложившего их финского ученого), когда сами прототипы упорядочены в пространстве низкой размерности. Например, входные данные можно отобразить на упорядоченную двумерную сеть прототипов так, что появляется возможность визуализации многомерных данных.
Как и в случае с персептронами начать изучение нового типа обучения лучше с простейшей сети, состоящей из одного нейрона.
Оценка вычислительной сложности обучения
В этой лекции мы рассмотрели два разных типа обучения, основанные на разных принципах кодирования информации выходным слоем нейронов. Логично теперь сравнить их по степени вычислительной сложности и выяснить когда выгоднее применять понижение размерности, а когда - квантование входной информации.
Как мы видели, алгоритм обучения сетей, понижающих размерность, сводится к обычному обучению с учителем, сложность которого была оценена ранее. Такое обучение требует









Кластеризация или квантование требуют настройки гораздо большего количества весов - из-за неэффективного способа кодирования. Зато такое избыточное кодирование упрощает алгоритм обучения. Действительно, квадратичная функция ошибки в этом случае диагональна, и в принципе достижение минимума возможно за





При одинаковой степени сжатия, отношение сложности квантования к сложности данных снижения размерности запишется в виде:

Рисунок 4.11 показывает области параметров, при которых выгоднее применять тот или иной способ сжатия информации.
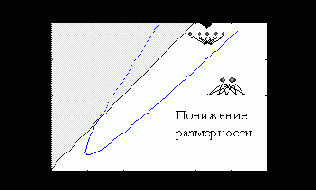
Рис. 4.11. Области, где выгоднее использовать понижение размерности или квантование
Наибольшее сжатие возможно методом квантования, но из-за экспоненциального роста числа кластеров, при большой размерности данных выгоднее использовать понижение размерности. Максимальное сжатие при понижении размерности равно



В качестве примера рассмотрим типичные параметры сжатия изображений в формате JPEG.
При этом способе сжатия изображение разбивается на квадраты со стороной





размерности. 3)
Однако, при увеличении размеров элементарного блока, появляется область высоких степеней сжатия, достижимых лишь с использованием квантования. Скажем, при




Победитель забирает не все
Один из вариантов модификации базового правила обучения соревновательного слоя состоит в том, чтобы обучать не только нейрон-победитель, но и его "соседи", хотя и с меньшей скоростью. Такой подход - "подтягивание" ближайших к победителю нейронов - применяется в топографических картах Кохонена. В силу большой практической значимости этой нейросетевой архитектуры, остановимся на ней более подробно.
Победитель забирает все
В Хеббовском и производных от него алгоритмах обучения активность выходных нейронов стремится быть по возможности более независимой друг от друга. Напротив, в соревновательном обучении, к рассмотрению которого мы приступаем, выходы сети максимально скоррелированы: при любом значении входа активность всех нейронов, кроме т.н. нейрона-победителя одинакова и равна нулю. Такой режим функционирования сети называется победитель забирает все.
Нейрон-победитель (с индексом





Количество нейронов в соревновательном слое определяет максимальное разнообразие выходов и выбирается в соответствии с требуемой степенью детализации входной информации. Обученная сеть может затем классифицировать входы: нейрон-победитель определяет к какому классу относится данный входной вектор.
В отличае от обучения с учителем, самообучение не предполагает априорного задания структуры классов. Входные векторы должны быть разбиты по категориям (кластерам) согласуясь с внутренними закономерностями самих данных. В этом и состоит задача обучения соревновательного слоя нейронов.
Постановка задачи
В простейшей постановке нейрон с одним выходом и d входами обучается на наборе d-мерных данных



Рис. 4.2. Сжатие информации линейным нейроном
Амплитуда этого выхода после соответствующего обучения (т.е. выбора весов по набору примеров

В простейшей постановке нейрон с одним выходом и d входами обучается на наборе d-мерных данных



Рис. 4.2. Сжатие информации линейным нейроном
Амплитуда этого выхода после соответствующего обучения (т.е. выбора весов по набору примеров

Итак, пусть теперь на том же наборе d-мерных данных


Рис. 4.5. Слой линейных нейронов
Мы хотим, чтобы амплитуды выходных нейронов были набором независимых индикаторов, максимально полно отражающих информацию о многомерном входе сети.
Правило обучения Хебба
Правило обучения отдельного нейрона-индикатора по-необходимости локально, т.е. базируется только на информации непосредственно доступной самому нейрону - значениях его входов и выхода. Это правило, носящее имя канадского ученого Хебба, играет фундаментальную роль в нейрокомпьютинге, ибо содержит как в зародыше основные свойства самоорганизации нейронных сетей.
Согласно Хеббу (Hebb, 1949), изменение весов нейрона при предъявлении ему примера пропорционально его входам и выходу:

или в векторном виде:

Если сформулировать обучение как задачу оптимизации, мы увидим, что обучающийся по Хеббу нейрон стремится увеличить амплитуду своего выхода:

где усреднение проводится по обучающей выборке

Указанное различие в целях обучения носит принципиальный характер, т.к. минимум ошибки

Правило обучения Ойа
От этого недостатка, однако, можно довольно просто избавиться, добавив член, препятствующий возрастанию весов. Так, правило обучения Ойа:

или в векторном виде:

максимизирует чувствительность выхода нейрона при ограниченной амплитуде весов. В этом легко убедиться, приравняв среднее изменение весов нулю. Умножив затем правую часть на w, видим, что в равновесии:


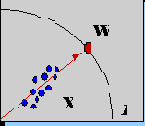
Рис. 4.3. При обучении по правилу Ойа, вектор весов нейрона располагается на гипер-сфере в направлении, максимизирующем проекцию входных векторов
Отметим, что это правило обучения по существу эквивалентно дельта-правилу, только обращенному назад - от входов к выходам (т.е. при замене

Эту же ситуацию можно описать и по-другому. Представим себе персептрон с одним (здесь - линейным) нейроном на скрытом слое, в котором число входов и выходов совпадает, причем веса с одинаковыми индексами в обоих слоях одинаковы. Будем учить этот персептрон воспроизводить в выходном слое значения своих выходов. При этом, дельта-правило обучения верхнего (а тем самым и нижнего) слоя примет вид правила Ойа:


Рис. 4.4. Автоассоциативная сеть с узким горлом - аналог правила обучения Ойа
Таким образом, существует определенная параллель между самообучающимися сетями и т.н. автоассоциативными сетями, в которых учителем для выходов являются значения входов. Подобного рода нейросети с узким горлом также способны осуществлять сжатие информации.
Предикторы
Условие максимизации совместной энтропии выходов можно переписать в виде:

Условные вероятности, входящие в это выражение, характеризуют разброс предсказаний каждого выхода, основанного на знании других выходов, стоящих справа от горизонтальной черты. Предположим, что мы используем дополнительные сети-предикторы, по одной для каждого выхода, специально обучаемые такому предсказанию (рисунок 4.9).

Рис. 4.9. Выделение независимых компонент с использованием предикторов
Обозначим



Отталкиваясь от значений


Таким образом, в заимном соревновании основная и дополнительные сети обеспечивают постепенное выявление статистически независимых признаков, осуществляющих оптимальное кодирование.
Размер сетей-предикторов определяется количеством выходов сети m, так что их суммарный объем, как правило, много меньше, чем размер декодера в автоассоциативной сети, определяемый числом входов d. В этом и состоит основное преимущества данного подхода.
Самообучающийся слой
В нашей трактовке правила обучения отдельного нейрона, последний пытается воспроизвести значения своих входов по амплитуде своего выхода. Обобщая это наблюдение, логично было бы предложить правило, по которому значения входов восстанавливаются по всей выходой информации. Следуя этой линии рассуждений получаем правило Ойа для однослойной сети:

или в векторном виде:

Такое обучение эквивалентно сети с узким горлом из скрытых линейных нейронов, обученной воспроизводить на выходе значения своих входов.

Рис. 4.6. Автоассоциативная сеть с узким горлом - аналог правила обучения Ойа
Скрытый слой такой сети, так же как и слой Ойа, осуществляет оптимальное кодирование входных данных, и содержит максимально возможное при данных ограничениях количество информации.
Сети радиального базиса
Самообучающиеся сети, рассмотренные в этой лекции, широко используются для предобработки данных, например при распознавании образов в пространстве очень большой размерности. В этом случае для того, чтобы процедура обучения с учителем была эффективна, требуется сначала сжать входную информацию тем или иным способом: либо выделить значимые признаки, понизив размерность, либо произвести квантование данных. Первый путь просто понижает число входов персептрона. Второй же способ требует отдельного рассмотрения, поскольку лежит в основе очень популярной архитектуры - сетей радиального базиса (radial basis functions - RBF).
Соревнование нейронов: кластеризация
В начале данной лекции мы упомянули два главных способа уменьшения избыточности: снижение размерности данных и уменьшение их разнообразия при той же размерности. До сих пор речь шла о первом способе. Обратимся теперь к второму. Этот способ подразумевает другие правила обучения нейронов.
Сравнение с традиционным статистическим анализом
Вывод о способности нейронных сетей самостоятельно выделять наиболее значимые признаки в потоках информации, обучаясь по очень простым локальным правилам, важен с общенаучной точки зрения. Изучение этих механизмов помогает глубже понять как функционирует мозг. Однако есть ли в описанных выше нейроалгоритмах какой-нибудь практический смысл?
Действительно, для этих целей существуют хорошо известные алгоритмы стандартного статистического анализа. В частности, анализ главных компонент также выделяет основные признаки, осуществляя оптимальное линейное сжатие информации. Более того, можно показать, что сжатие информации слоем Ойа эквивалентно анализу главных компонент . Это и не удивительно, поскольку оба метода оптимальны при одних и тех же ограничениях.
Однако стандартный анализ главных компонент дает решение в явном виде, через последовательность матричных операций, а не итерационно, как в случае нейросетевых алгоритмов. Так что при отсутствии высокопараллельных нейроускорителей на практике удобнее пользоваться матричными методами, а не обучать нейросети. Есть ли тогда практический смысл в изложенных выше итеративных нейросетевых алгоритмах?
Конечно же есть, по крайней мере по двум причинам:
Во-первых, иногда обучение необходимо проводить в режиме on-line, т.е. на ходу адаптироваться к меняющемуся потоку данных. Примером может служить борьба с нестационарными помехами в каналах связи. Итерационные методы идеально подходят в этой ситуации, когда нет возможности собрать воедино весь набор примеров и произвести необходимые матричные операции над ним. Во-вторых, и это, видимо, главное, нейроалгоритмы легко обобщаются на случай нелинейного сжатия информации, когда никаких явных решений уже не существует. Никто не мешает нам заменить линейные нейроны в описанных выше сетях - нелинейными. С минимальными видоизменениями нейроалгоритмы будут работать и в этом случае, всегда находя оптимальное сжатие при наложенных нами ограничениях. Таким образом, нейроалгоритмы представляют собой удобный инструмент нелинейного анализа, позволяющий относительно легко находить способы глубокого сжатия информации и выделения нетривиальных признаков.
Иногда,даже простая замена линейной функции активации нейронов на сигмоидную в найденном выше правиле обучения:

приводит к новому качеству (Oja, et al, 1991). Такой алгоритм, в частности, с успехом применялся для разделения смешанных неизвестным образом сигналов (т.н. blind signal separation). Эту задачу каждый из нас вынужден решать, когда хочет выделить речь одного человека в шуме общего разговора.
Однако нас здесь интересуют не конкретные алгоритмы, а, скорее, общие принципы выделения значимых признаков, на которых имеет смысл остановиться несколько более подробно.
Упорядочение нейронов: топографические карты
До сих пор нейроны выходного слоя были неупорядочены: положение нейрона-победителя в соревновательном слое не имело ничего общего с координатами его весов во входном пространстве. Оказывается, что небольшой модификацией соревновательного обучения можно добиться того, что положение нейрона в выходном слое будет коррелировать с положением прототипов в многомерном пространстве входов сети: близким нейронам будут соответствовать близкие значения входов. Тем самым, появляется возможность строить топографические карты чрезвычайно полезные для визуализации многомерной информации. Обычно для этого используют соревновательные слои в виде двумерных сеток. Такой подход сочетает квантование данных с отображением, понижающим размерность. Причем это достигается с помощью всего лишь одного слоя нейронов, что существенно облегчает обучение.
В этой лекции мы познакомились
В этой лекции мы познакомились со вторым из двух главных типов обучения - обучением без учителя. Этот режим обучения чрезвычайно полезен для предобработки больших массивов информации, когда получить экспертные оценки для обучения с учителем не представляется возможным. Самообучающиеся сети способны выделять оптимальные признаки, формируя относительно малоразмерное пространство признаков, без чего иногда невозможно качественное распознавание образов. Таким образом, оба типа обучения удачно дополняют друг друга. Кроме того, как мы убедились на примере сетей с узким горлом, между этими типами обучения существует тесная взаимосвязь: если посмотреть на ситуацию под определенным углом зрения, соответствующие правила обучения подчас просто совпадают.
Взаимодействие нейронов: анализ главных компонент
Единственный нейрон осуществляет предельное сжатие многомерной информации, выделяя лишь одну скалярную характеристику многомерных данных. Каким бы оптимальным ни было сжатие информации, редко когда удается полностью охарактеризовать многомерные данные всего одним признаком. Однако, наращиванием числа нейронов можно увеличить выходную информацию. В этом разделе мы обобщим найденное ранее правило обучения на случай нескольких нейронов в самообучающемся слое, опираясь на отмеченную выше аналогию с автоассоциативными сетями.
Активная кластеризация
Итак, мы установили, что преобразование информации рекуррентными нейронными сетями минимизирующими энергию может приводить к появлению в их пространстве состояний аттракторов, далеких по форме от образов внешнего для сети окружения. Таким образом, в отличие от рассмотренной в прошлой лекции кластеризации, осуществляемой сетями без обратных связей, появляется возможность использовать рекуррентные сети для активной кластеризации, при которой сеть "творчески" относится к входным векторам, осуществляя нетривиальные обобщения поступающих на ее вход сигналов.
Теоретическим основанием такой активной кластеризации является отмеченное выше наблюдение, что все устойчивые состояния сети Хопфилда могут быть проинтерпретированы единым образом, как локально наилучшие версии одного сообщения, переданного через канал с шумом. Если предъявить сети эти сообщения, использованные для формирования ее связей, в качестве начальных состояний, она расклассифицирует их, отнеся к той или иной версии прототипа. (Такая классификация при асинхронной динамике будет в общем случае нечеткой - одно и то же начальное состояние в разных попытках может эволюционировать к разным аттракторам).
Однако, если исследовать все пространство состояний сети, предъявляя ей не ранее заучиваемые, а случайно сгенерированные векторы, то в нем могут обнаружиться такие аттракторы, которые не притягивают ни одного вектора из заучиваемого набора. Подобные аттракторы можно назвать пустыми классами, сформированными сетью. Понятие пустого класса не совпадает с понятием ложного состояний памяти. Последние не всегда описывает пустой класс. Например, когда в сети на основе слегка искаженных сообщений генерируется единственная версия сообщения, не совпадающая ни с одним из них (ложное состояние), но притягивающее все полученные сообщения (не пустой класс).
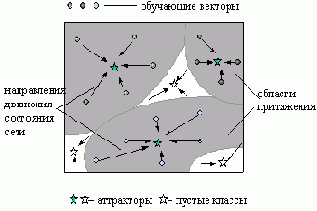
Рис. 5.8. Пространство состояний сети с пустыми классами
Аттракторы, являющиеся центрами притяжения состояний, относящихся к пустым классам, предоставляют нам совершенно новую информацию. Действительно, они предсказывают существование новых классов объектов, которые не имеют своих представителей в полученных сетью сообщениях.
Известным примером такой предсказательной категоризации является периодическая система элементов Менделеева, в которой изначально были определены три пустые клетки для впоследствии обнаруженных новых химических элементов. Итак, минимизирующие энергию нейронные сети типа сети Хопфилда могут использоваться для предсказания существования новых классов объектов.
Анализ голосований
В качестве иллюстрации приведем результаты кластеризации данных по голосованиям в ООН в 1969-1970гг. В данном примере анализировались голосования по 14 резолюциям для 19 стран. Сеть, производившая кластеризацию стран по степени схожести их голосований, состоит из нейронов, состояния которых представляют картину голосования одного из участников по отобранным 14 резолюциям (да и нет соотносились с бинарными состояниями нейронов). Этой сети предъявлялись результаты голосований 19 стран - членов ООН, которые сформировали матрицу связей сети по правилу Хебба. Результаты категоризации входных векторов (а тем самым - и соответствующих стран), этой нейронной приведены в таблице:
| США | 0 | Югославия | 2 | Болгария | 4 | ??? | 0 |
| Новая Зеландия | 2 | Кения | 2 | СССР | 5 | ||
| Великобритания | 3 | ОАР | 2 | Сирия | 6 | ||
| Албания | 4 | Дагомея | 9 | Танзания | 7 | ||
| Бразилия | 5 | Сенегал | 9 | ||||
| Норвегия | 5 | ||||||
| Мексика | 6 | ||||||
| Швеция | 7 | ||||||
| Венесуэла | 8 | ||||||
| Франция | 9 |
Все используемые при обучении страны разделились на три легко интерпретируемых класса (условно: "капиталистические", "неприсоединившиеся" и "социалистические"), то есть кодирующие их голосования векторы-состояния эволюционируют к одному из трех стационарных состояний (локально наилучших версий прототипа "страна - член ООН"). Хэммингово расстояние от соответствующих состояний до притягивающих их аттракторов приведено в колонках "ранг".
У сети, однако, имеется и четвертое стационарное состояние, не притягивающее ни один из 19 образов, используемых при построении матрицы связей сети. Это состояние может рассматриваться как описывающее совершенно новую группу стран, в которую не входят ни одна из рассматриваемых. Мы можем описать эту группу, изучив вид соответствующего аттрактора - центра пустого четвертого класса. Действительно, такое изучение легко выявляет тот факт, что представители этого нового класса должны были бы иметь по сравнению с учтенными странами совершенно особое мнение при голосовании по корейскому вопросу. Учитывая то, что ни Южная, ни Северная Корея до сих пор не представлены в ООН, интерпретация этого класса является прозрачной. Очевидно, что подобный подход может использоваться при анализе экономических, социологических, демографических и других данных. В частности он может использоваться для поиска новых потенциальных и свободных мест на рынках, в политическом спектре и пр.
Учитывая то, что ни Южная, ни Северная Корея до сих пор не представлены в ООН, интерпретация этого класса является прозрачной. Очевидно, что подобный подход может использоваться при анализе экономических, социологических, демографических и других данных. В частности он может использоваться для поиска новых потенциальных и свободных мест на рынках, в политическом спектре и пр.
 |
 |
 |
Вообще говоря, еще задолго до этого, в 1954г. Крэгг и Темперли указали на аналогию между стационарной активностью нейронных сетей и коллективными состояниями в системах магнитных диполей, а в 1974 году Литтл также провел аналогию между нейронными сетями и спиновыми системами и указал на аналогию шума и температуры. Но ряд обстоятельств, в частности, связанных с другим характером динамики нейронов, другим типом возникающих в сети аттракторов и, главным образом, недостаточно четкая физическая аналогия, не позволили этим исследователям оказать на развитие теории нейронных сетей того влияния, какое оказала на него работа Хопфилда.
2)
Ранее мы определяли обучение по Хеббу как такое, при котором изменение веса

3)
Всего существует 402 типа булевых функций четырех переменных, к которым сводится все множество из 65536 функций.


Асинхронная динамика
Нейроны в модели Хопфилда, подобно спиновым переменным, могут принимать два состояния



При выполнении условия


В другом варианте - последовательной динамике - перебор нейронов производится не случайным образом а циклически, но в каждый момент времени также может изменяться состояние лишь одного нейрона. Эти два варианта качественно отличаются от параллельной динамики, подразумевающей одновременное изменение состояний всех тех нейронов, для которых выполняется условие

В отличие от многослойных сетей, в которых входные и выходные нейроны пространственно разделены в модели Хопфилда все нейроны одновременно являются и входными, и скрытыми, и выходными. Роль входа в таких сетях выполняет начальная конфигурация активностей нейронов, а роль выхода - конечная стационарная конфигурация их активностей.
Ассоциативная память
Аттракторами сети Хопфилда являются стационарные состояния. Если начальная конфигурация






Важным свойством такой памяти, представленной набором аттракторов сети, является ее распределеннсть. Это означает, что все нейроны сети участвуют в кодировании всех состояний памяти. Поэтому небольшие искажения значений отдельных весов не сказываются на содержании памяти, что повышает устойчивость памяти к помехам.
Конечно, ассоциативная память может быть реализована и без использования нейронных сетей. Для достаточно с помощью обычного компьютера осуществить последовательное сравнение внешнего стимула со всеми предварительно запомненными образами, выбрав из них тот, для которого Хэммингово расстояние до входного сигнала минимально. Однако, сеть Хопфилда позволяет исключить перебор состояний памяти и осуществить эту процедуру параллельным способом, при котором время выборки из памяти не увеличивается с ростом числа запомненных образов.
Исторический поворот в 1982 году
В 1982 году в докладах Американской академии наук была опубликована статья американского физика, специалиста в области физики твердого тела из Калифорнийского Технологического Института, Джона Хопфилда (Hopfield, 1982a). С этой работы начался бурный процесс возрождения интереса к искусственным нейронным сетям, на который так негативно повлияла в конце шестидесятых книга Минского и Пейперта. В работе Хопфилда впервые было обращено внимание на аналогию, которая существует между сетями с симметричными связями и давно известными физикам объектами - спиновыми стеклами. Кроме того, стало ясно, что такие сети служат прекрасной основой для построения моделей содержательно-адресованной памяти. И наконец, обнаружилось, что нейронные сети могут быть успешно исследованы с помощью методов теоретической физики, в частности, статистической механики. Результатом этого обстоятельства явилось массовое внедрение физиков и физических методов в эту новую область знания. 1)
Энергия состояния
Нетрудно показать, что описанная выше асинхронная динамика сети сопровождается уменьшением энергии сети, которая определяется следующим образом:

Действительно, при изменении состояния одного -го нейрона его вклад в энергию изменяется с



В случае, когда нейрон имеют ненулевые пороги активации


Поскольку число нейронов в сети конечно, функционал энергии ограничен снизу. Это означает, что эволюция состояния сети должна закончиться в стационарном состоянии, которому будет соответствовать локальный минимум энергии. В Хопфилдовской модели стационарные конфигурации активностей нейронов являются единственным типом аттракторов в пространстве состояний сети. Мы можем представить динамику сети, сопоставив ее состояние с шариком, движущимся с большим трением в сложном рельефе со множеством локальных минимумов. Сами эти минимумы будут устойчивыми состояниями памяти, а окружающие точки на склонах - переходными состояниями.

Рис. 5.4. Поведение состояния в сети Хопфилда аналогично движению шарика, скатывающегося со склона в ближайшую лунку. Начальное состояние шарика соответствует вектору, содержащему неполную информацию об образе памяти, которому отвечает дно лунки
Такая динамика определяет главное свойство сети Хопфилда - способность восстанавливать возмущенное состояние равновесия - "вспоминать" искаженные или потерянные биты информации. Восстановление полной информации по какой-либо ее части - вспоминание по ассоциации - наделяет модель Хопфилда свойством ассоциативной памяти. (Далее в этой лекции мы продемонстрируем, и более общие возможности сети Хопфилда.)
Метод Кинцеля. Уничтожение фрустрированных связей.
"Ложная память" имеет интересный нетривиальный смысл и в случае использования других правил обучения, минимизирующих энергию нейронных сетей.
Одно из них было предложено в 1985 году Кинцелем, который основывал свои рассуждения на реальном наблюдении, согласно которому у ребенка в первые несколько лет жизни отмирает большое число синапсов, хотя именно в это время он учится и усваивает огромное количество информации (Kinzel, 1985). Подобное явление подсказало Кинцелю следующий метод обучения. Возьмем полностью неорганизованную сеть нейронов




Требование нефрустрированности каждой связи для всех запоминаемых векторов, конечно, очень сильное. Для слабо коррелированных образов приходится уничтожать так много межнейронных соединений, что в полученной слабосвязанной сети почти все состояния оказываются стабильными, т.е. появляется большое число "ложных" образов. (Если нейроны вообще не связаны -

метода уничтожения фрустрированных связей, который стартует с сети, у которой величины всех синаптических связей положительны и равны между собой, и не уничтожает, а инвертирует знак связи, фрустрированной во всех запоминаемых состояний. В примере, иллюстрируемом приводимым ниже рисунком,
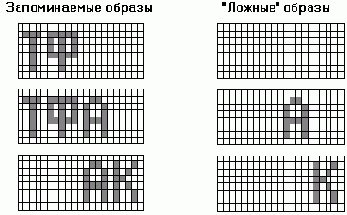
Рис. 5.5. Слева - состояния, запоминаемые в сети Кинцеля . Справа - "ложные" образы
в сети из 168 нейронов, организованных в двумерную структуру, запоминаются три образа: (ТФ__) (ТФА_) и (__АК). "Ложными" образами для сети с минимальной памятью будут при этом: пустое поле (____); (__А_); (___К) и их негативы. Невозможно раздельное появление в образе памяти (Т___) и (_Ф__), так как им соответствует один вектор минимального базиса. Невозможно также появление стационарного состояния (ТФ_К), так как в заучиваемых образах присутствие (ТФ__) исключает присутствие (___К) и наоборот.
Метрика пространства состоянний
Расстояние между состояниями сети можно измерять в т.н. метрике Хэмминга. Если два вектора






В случае спиновых переменных,






Минимальный базис
Состояния ложной памяти могут иметь и другие, не менее интересные формы. Рассмотрим, например, вариант модели Хопфилда, в котором состояния нейронов принимают значения 0 или 1. Подобная модель легко переформулируется в оригинальную, для которой состояниями являются спиновые переменные


Рассмотрим следующий набор векторов:





сети Хопфилда. Если найти все аттракторы этой сети (что нетрудно сделать в виду небольшой размерности пространства его состояний 27=128 ), то обнаружится, что помимо векторов ,







Векторы




Векторы


Кроме того, все стационарные состояния сети, в Хеббовские связи которых записаны векторы


Используя векторы минимального базиса можно получить новый вид недиагональных элементов Хеббовской матрицы связей

где

С помощью этого представления можно получить необходимые условия стационарности состояний сети. В частности, условие того, что сеть будет генерировать в качестве аттракторов векторы минимального базиса, легко формулируется в терминах матричных элементов





Для рассмотренного нами выше примера эта матрица имеет вид

Модель Крика - Митчисона. Разобучение
В 1983 году в журнале Nature одновременно появились две публикации (Hopfield, Feinstein & Palmer 1983 и Crick & Mitchison, 1983), в которых была описана процедура уменьшения доступа к состояниям ложной памяти и ее возможная биологическая интерпретация. Эта процедура, названная разобучением, применяется к уже обученной сети, в пространстве которой есть ложные состояния. Она предполагает многократное предъявление сети в качестве начальных состояний случайно сгенерированных векторов и прослеживание их эволюции вплоть до стационарного состояния



Хопфилд с коллегами установили, что применение такой процедуры к сети, обученной по правилу Хебба на наборе случайных векторов, приводит к увеличению и выравниванию доступности состояний, соответствующих запоминаемым образам, и снижению доступности состояний ложной памяти. Эти явления они объяснили тем, что в рассматриваемом случае состояниям ложной памяти соответствуют гораздо более "мелкие" энергетические минимумы, чем состояниям, соответствующим запоминаемым образом. Поэтому ложные состояния сильнее подвержены разобучению, которое выражается в "закапывании" энергетических минимумов, в которые попадает система. Выравнивание доступности состояний памяти объясняется тем, что состояния с большими областями притяжения чаще притягивают случайный стимул и их область притяжения уменьшается быстрее, чем у состояний с меньшими сферами притяжения.
Крик и Митчисон, кроме того, предположили, что процесс, аналогичный разобучению, происходит в мозгу человека и животных во время фазы быстрого (парадоксального) сна, для которого характерны фантастические сюжеты (составленные из аналогов ложных образов). В этот период кора головного мозга постоянно возбуждается случайными воздействиями ствола мозга, и возникающие картины далеки от тех, которые дает сенсорный опыт. Разобучение при этом эффективно приводит к забыванию подобных парадоксальных картин и к увеличению доступа к образам, соответствующим объектам внешнего мира.
Гипотеза о роли быстрого сна была сформулирована Криком и Митчисоном в виде афоризма: "Мы грезим, чтобы забыть".
Идея разобучения затем была развита другими исследователями. В одном из ее вариантов в качестве начальных состояний сети предъявляются не случайные стимулы, а зашумленные случайным шумом запоминаемые образы. При этом, помимо разобучения сети финальным аттрактором, она слегка подучивается запоминаемым образом


То есть, если образ памяти восстанавливается без ошибки, синаптические связи не модифицируются. Подобная модификация процедуры разобучения может существенно увеличить емкость памяти (с


Неустранимость ложной памяти. Запрещенные наборы
Мы рассмотрели Хеббовское и Кинцелевское правила построения синаптических связей и убедились, что соответствующие сети демонстрируют нетривиальное отображение множества заучиваемых образов на множество аттракторов сети. В частности, ряд аттракторов далеки от заучиваемых образов и квалифицируются как ложная память. Возникает естественный вопрос о существовании такого метода обучения, который вообще бы устранял дополнительную память.
Оказывается, что ответ на него в общем случае отрицательный. Имеются такие наборы образов, что какую бы матрицу синаптических связей и пороги нейронов, гарантирующие их стационарность, мы не выбрали, в сети с неизбежностью возникнут иные аттракторы.
В частности, уже в сети из трех нейронов невозможно обеспечить стационарность только следующих четырех состояний: (0,0,0), (1,1,0), (1,0,1) и (0,1,1) или симметричного набора состояний. Такие наборы векторов, которые не могут составлять и исчерпывать память сети, называют запрещенными. Можно показать, что для сети из трех нейронов два приведенных выше множества векторов исчерпывают все запрещенные наборы образов.
В сети из четырех нейронов не реализуемы уже 40 наборов векторов, но все они могут быть получены всего из двух независимых наборов преобразованием однотипности - перестановками переменных и инверсией.1)
Такая тенденция является обнадеживающей с точки зрения возможностей сетей к запоминанию образов, поскольку доля не реализуемых функций падает. Однако сети, аттракторы которых сконструированы заранее, могут имитировать только ассоциативную память, не создающую новой информации. Нас же сейчас интересует как раз эффект обобщения, присущий рекуррентным сетям, так же как и обычным персептронам.
Обучение сети. Правило Хебба
Описанная сеть действительно стала использоваться для моделирования ассоциативной памяти, поскольку уже в первой своей работе Хопфилд указал конструктивный метод построения синаптических связей между нейронами, который в некоторых случаях позволял запомнить любые заранее заданные состояния сети.
Например, полезной была бы сеть, аттракторы которой, соответствовали бы векторам, кодирующим бинарные изображения подписей различных людей на чеке. Поскольку практически невозможно одинаково расписаться дважды, подобная сеть была бы незаменима при распознавании подписи, несмотря на ее естественные вариации. Если число различных типов подписей, которые должна распознавать сеть, равно P и образцы в некотором смысле типичных, наиболее вероятных или усредненных подписей различных людей кодируются векторами

Хопфилд предложил использовать для решения этой задачи Хеббовское правило построения межнейронных связей. 1)

Это правило действительно гарантирует стационарность произвольно выбранных векторов






Аттракторам, не совпадающим с векторами

поиск промоторов в ДНК
Промоторами называются области четырехбуквенной последовательности ДНК (построенной из нуклеотидов A,T,G,C), которые предшествуют генам. Эти области состоят из 50-70 нуклеотидов и распознаются специальным белком РНК-полимеразой. Полимераза связывается с промотором и транскрибирует ее (расплетает на две нити). У кишечной палочки, например, обнаружено около трехсот различных промоторов. Несмотря на различие, эти области имеют некоторые похожие участки, которые представляют собой как бы искажения некоторых коротких последовательностей нуклеотидов (например, бокс Гильберта - TTGACA и бокс Прибноу - TATAAT). Поэтому основные методы распознавания промоторов основываются на представлении о консенсус-последовательности: некотором идеальном промоторе, искажениями которого являются реальные промоторы. Близость некоторой последовательности к консенсус-последовательности оценивается по значению некоторого индекса гомологичности. Очевидно, что представление о версии-прототипа в теории минимизирующих энергию нейронных
сетей прямо соответствует представлению о консенсус-последовательности.
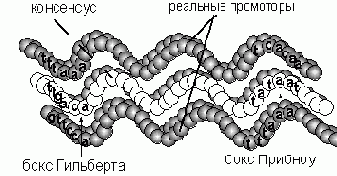
Рис. 5.7. Идеальный промотор - консенсус-последовательность (в середине) является аналогом единственной версии прототипа - аттрактора в сети Хопфилда, выработанной в ней при записи зашумленных сообщений (аналогов реальных промоторов: сверху и снизу). Аналогом гомологического индекса, определяющего близость реальных промоторов к консенсус-последовательности, является энергия состояния сети
Поэтому сеть Хопфилда, например, может непосредственно использоваться для ее поиска. Более того, оказывается, что энергия состояния сети может использоваться в качестве аналога гомологического индекса при оценке близости последовательности промотора к консенсус-последовательности. Такой подход позволил создать новый, весьма эффективный нейросетевой метод поиска промоторов. Аналогичный подход может использоваться для поиска скрытых повторов в ДНК и реконструкции эволюционных изменений в них.
Хотя молекулярная генетика представляет собой достаточно специфическую область применения методов обработки информации, она часто рассматривается как показательный пример приложений такой информационной технологии, как Извлечение Знаний из Данных (Data Mining). Применение для этих целей нейросетевых методов мы рассмотрим более подробно в отдельной лекции.
Симметричность связей
В Хопфилдовской сети матрица связей между нейронами



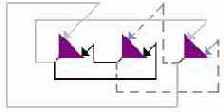
Рис. 5.3. Архитектура сети Хопфилда. Связи с одинаковым весом обозначены одинаковыми линиями. Матрица соединений полносвязанная и симметричная. Самовоздействие нейронов отсутствует
Спиновые стекла
В кристаллической решетке атомы, обладающие магнитными моментами, могут взаимодействовать друг с другом различными способами. Если связи между моментами таковы, что стремятся сориентировать их параллельно, то в основном состоянии (состоянии минимальной энергии) все атомы в решетке ориентируют свои моменты параллельно. Такие вещества называются ферромагнетиками. Связи между атомами описываются при этом одинаковыми положительными числами и называются также ферромагнитными. Если, напротив, все связи отрицательны, то такие вещества называются антиферромагетиками. В антиферромагнетиках соседние спины ориентируются в противоположных направлениях. А вот если связи между магнитными моментами атомов имеют случайные значения знаков, то соответствующие системы называются спиновыми стеклами (см. рисунок 5.1). Основная особенность системы связей в спиновых стеклах такова, что система в целом оказывается фрустрированной.
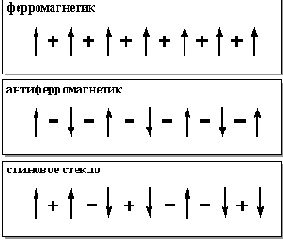
Рис. 5.1. Знаки связей между спинами в ферромагнетике, антиферромагнетике и спиновом стекле
Фрустрация ("разочарование") означает, что как бы ни сориентировались отдельные магнитные моменты атомов в спиновом стекле, всегда найдутся такие пары из них, в которых взаимодействие вносит положительный (разочаровывающий) вклад в энергию состояния (см. рисунок 5.2).
Фрустрированность системы обусловливает огромное вырождение ее основного состояния. Спиновое стекло может "замерзнуть" в любом из возможных основных состояний системы, отличающемся от множества других аналогичных состояний с практически такой же энергией лишь конфигурацией системы магнитных моментов. Хопфилд предположил, что аналогичное явление может лежать в основе существования огромного числа состояний памяти, характерного для мозга. Действительно, можно рассмотреть модель полносвязной нейронной сети с рекуррентными симметричными связями между нейронами. В такой модели возбуждающим связям будут соответствовать ферромагнитные связи в спиновом стекле, а тормозным - антиферромагнитные связи.
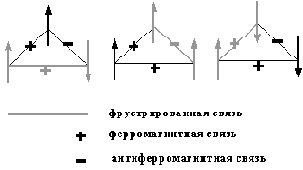
Рис. 5.2. Фрустрированная система трех взаимодействующих спинов. При любых их ориентациях всегда находится такая связь , знак которой противоречит взаимной ориентации пары, что приводит к нежелательному положительному вкладу в полную энергию системы
Подобно спиновым стеклам, такие сети будут иметь множество стационарных конфигураций активностей нейронов, являющихся аттракторами (от англ. attract - притягивать), т.е. такими состояниями, к которым сходится динамика нейросети. Именно введенная Хопфилдом динамика изменений состояний нейронов наряду с симметричностью связей между нейронами определили новизну описываемой модели.
Версии протитипа
Итак, структура аттракторов в модели Хопфилда может допускать различные содержательные интерпретации. В том случае, когда она совпадает со структурой запоминаемых образов мы говорим об ассоциативной памяти (пассивной). Если, напротив, в сети формируется единственный аттрактор, в каком-то смысле являющийся прототипом этих образов, то проявляется способность сети к обобщению (generalization). В общем же случае структура аттракторов сети настолько сложна, что на первый взгляд не допускает какой-либо наглядной трактовки. Действительно, такая трактовка должна быть настолько универсальной, чтобы включать режимы запоминания и обобщения в качестве предельных случаев. Тем не менее она возможна и опирается на рассуждения, которые приводятся в данном разделе.
Начнем с рассмотрения сети Хопфилда, в память которой, согласно правилу Хебба, записан только один образ


У такой сети есть только два зеркально симметричных стационарных состояния


Заметим, что все связи в сети дают в энергию одинаковый отрицательный вклад и поэтому являются не фрустрированными. Напомним, что условием фрустрации связи в состоянии сети является неравенство

Именно это условие не выполняется ни для одной связи в сети с записанным единственным образом. Мы можем трактовать подобную ситуацию так, что сеть с одним записанным в нее образом точно воспроизводит его в виде своего аттрактора (с точностью до зеркального отражения), и если мы выберем в этой сети случайную связь, то вероятность ее фрустрации будет равна нулю.
Таким образом, сеть Хопфилда идеально приспособлена для хранения единственного образа.
Рассмотрим теперь следующую систему (см. рисунок 5.6). Пусть в Хопфилдовской сети-передатчике (слева) записан единственный образ


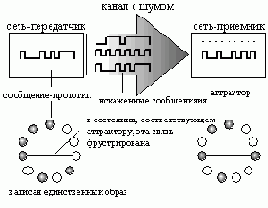
Внизу: сети с записанным единственным сообщением прототипом (слева) и со всеми искаженными версиями этого сообщения (справа)" width="313" height="243">
Рис. 5.6. Вверху: интерпретация стационарных состояний в сети Хопфилда как локально наиболее правдоподобных версий сообщения, многократно переданного сетью-передатчиком в сеть-приемник через канал с шумом. Внизу: сети с записанным единственным сообщением прототипом (слева) и со всеми искаженными версиями этого сообщения (справа)
Задача сети-премника состоит в том, чтобы имея P полученных сообщений






Вспоминая выражение для правила Хебба, убеждаемся что если сообщения


Используя последнее соотношение, преобразуем выражение для энергии состояния в сети-приемнике к виду

Поскольку мы не знаем точного вида сообщения



Таким образом, энергия состояния сети-приемника с точностью до постоянных множителя и слагаемого совпадает с вероятностью фрустрации случайно выбранной связи в сети-передатчике, оцененной по полученным от нее сообщениям.
Однако в сети-передатчике записано лишь одно сообщение, и вероятность фрустрации связей в ней равна нулю. Но поскольку ни сообщение, ни соответствующие ему связи сети-передатчика нам не известны, мы можем лишь пытаться найти такое состояние сети-приемника, которое хотя бы локально минимизирует эту вероятность. Подобные состояния были бы локально наилучшими версиями сообщения, посылаемого сетью-передатчиком.
А так как вероятность нахождения фрустрированной связи в передатчике связана с энергией состояния в приемнике, то такими наилучшими версиями как раз и окажутся состояния, соответствующие энергетическим минимумам сети-приемника. Таким образом все аттракторы сети Хопфилда, связи которой сформированы согласно правилу Хебба, исходя из набора обучающих векторов

Подобный подход устраняет деление состояний памяти на истинные и ложные, давая им единую интерпретацию. В такой трактовке функционирование сети Хопфилда в качестве пассивной памяти соответствует случаю, когда шум в канале очень велик, т.е. все принимаемые сетью сообщения некоррелированы. Это не дает ей возможности выделить из них сообщения и, рассматривая их как равноправные его версии, сеть генерирует аттрактор в каждой точке N-мерного пространства

Хотя первоначально сеть Хопфилда привлекалась для объяснения свойств ассоциативной памяти, можно привести множество различных примеров ее применения и для выделения зашумленного сигнала-прототипа. В качестве одного из таких примеров мы рассмотрим один - поиск промоторов в ДНК
Выделение сигнала из шума
Разобучение действительно улучшает запоминание случайных образов. Однако, например, для коррелированных образов доводы, приведенные в предыдущем разделе теряют свое значение. Действительно, если эти образы, например, являются слегка зашумленными вариантами одного образа-прототипа


Этот пример показывает, что ложная память иногда не бесполезна, а преобразуя заучиваемые векторы, дает нам некоторую важную информацию о них. В данном случае сеть как бы очищает ее от случайного шума. Подобное явление характерно и для обработки информации человеком. В известном психологическом опыте людям предлагается запомнить изображения, каждое из которых представляет собой обязательно искаженный равносторонний треугольник. При контрольной проверке на значительно более широком наборе образов, содержащийся в них идеальный равносторонний треугольник опознается испытуемыми как ранее виденный. Такое явление называется выработкой прототипа. Именно эта аналогия использовалась нами при введении обозначения

Добавление нового нейрона.
Со временем после нескольких циклов смещений накапливается информация, на основании которой принимается решение о месте, в котором должен быть добавлен новый нейрон. Каждый раз, когда для случайно выбранного города




Инициализация: генерируется кольцевая структура, состоящая из трех нейронов, имеющих случайное положение на плоскости. Осуществляется фиксированное число












Очевидно, что решение задачи может быть найдено не ранее того, как число нейронов в кольце достигнет числа городов





На шаге 2 необходимо проверить каждое звено цепи, чтобы найти то, которому соответствует максимальная суммарная ошибка концевых нейронов. Поскольку число звеньев равно числу нейронов, то число действий опять имеет порядок








Для улучшения квадратичной временной сложности описанного алгоритма Фритцке и Вильке модифицировали шаги 1-3. Они учли, что согласно численным экспериментам вначале кольцевая структура нейронов быстро распределяется по всей области размещения городов, и затем с ростом числа нейронов изменения приобретают локальный характер. Такое поведение натолкнуло их на идею заменить глобальный поиск нейрона-победителя на шаге 1 приближенной локальной процедурой. А именно: для каждого города запоминается тот нейрон, который наиболее часто оказывался к нему ближайшим, и если город выбран вновь, то поиск ближайшего к нему нейрона ограничивается этим нейроном и его ближайшими по кольцу соседями вплоть до порядка k. Поскольку k есть константа, то сложность поиска оказывается в этом случае


Рис. 6.3. Локальный поиск наилучшего нейрона: -предыдущий нейрон ; ближайшие его соседи вплоть до 2 порядка являются кандидатами в победители на следующем шаге
Для устранения на шаге 2 линейного поиска звена с максимальной ошибкой используется тот факт, что таким звеном является то, которое связывает нейроны, часто становящиеся победитями.
Третий шаг тоже можно модифицировать: если некоторый нейрон несколько раз оказывается ближайшим для данного города, значит для этого города структура кольца уже стабилизировалась и нейрон "приклеивается" к данному пункту маршрута. Это означает, что он совмещается со своим городом и больше уже не двигается.Город же удаляется из списка городов, разыгрываемых на шаге распределения. Когда этот список становится пустым процесс поиска маршрута заканчивается.
Таким образом, каждый шаг в цикле теперь требует постоянное число операций и временная сложность всего алгоритма становится порядка

Описанный эффективный нейросетевой подход (FLEXMAP) был протестирован на разных распределениях городов числом до 200 и неизменно находил маршруты, отличающиеся не более чем на 9% от оптимального.
Генетические алгоритмы
Эти алгоритмы могут использоваться для поиска экстремума нелинейных функций с множественными локальными минимумами. Они имитируют адаптацию живых организмов к внешним условиям в ходе эволюции. Точнее, они моделируют эволюцию целых популяций организмов и поэтому требуют достаточно больших ресурсов памяти и высокой скорости вычислительных систем. Важным достоинством их является то, что они не накладывают никаках требований на вид минимизируемой функции (например, дифференцируемость). Поэтому их можно применять в случаях, когда градиентные методы не применимы.
Генетические алгоритмы используют соответствующую терминологию, конфигурации системы называют хромосомами, над которой можно производить операции кроссинговера и мутации. Хромосома является основной информационной единицей, кодирующей переменную, относительно которой ищется оптимум. Обычно она представляет собой битовую строку, хотя компоненты этой строки могут иметь и более общий вид (для задачи коммивояжера компоненты хромосом представляют собой последовательность номеров городов в данном маршруте, например (145321)). Каждая компонента хромосомы называется геном. Выбор удачного представления для хромосомы, или же кодировка искомого решения, могут значительно облегчить нахождение решения.
Обучение происходит в популяции хромосом, к которым на каждом шаге эволюции применяются две основные операции. При мутациях в хромосоме случайным образом выбираются и изменяются ее компоненты (гены). При кроссинговере две хромосомы А и В разрезаются на две части в случайно выбранной одной точке




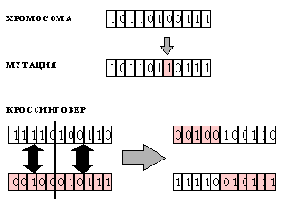
Рис. 6.4. Представление искомого решения в виде битовой строки - хромосомы (вверху). Операции мутации и кроссинговера (внизу)
После каждого шага эволюции - генерации, на котором мутируют и подвергаются кроссинговеру все хромосомы, для каждой из новых хромосом вычисляется значение целевого функционала, которое достигается на кодируемых ими решениях.
Чем меньше это значение для данной хромосомы, тем с большей вероятностью она отбираются для кроссинговера. В ходе эволюции усредненное по популяции значение функционала будет уменьшаться, и после завершения процесса (проведения заданного числа генераций) хромосома с минимальным его значаением выбирается в качестве приближенного решения поставленной задачи. Можно значительно улучшить свойства генетического алгоритма если после порождения новой генерации



Имитация отжига
В предыдущем разделе мы заметили, что переход от бинарных нейронов к аналоговым значительно улучшил свойства решения. Аналогичного эффекта можно добиться используя по-прежнему бинарные нейроны, но заменив детерминистскую динамику стохастической, характеризуемой некоторой эффективной температурой


Положительная роль температуры заключается в том, что шум позволяет системе покидать локальные минимумы энергии и двигаться в сторону более глубоких энергетических минимумов. Соответствующий (не нейросетевой) алгоритм оптимизации был предложен в 1953 г. и получил название имитации отжига (Metropolis et al., 1953). Этот термин происходит от названия способа выжигания дефектов в кристаллической решетке. Атомы, занимающие в ней неправильное место, при низкой температуре не могут сместиться в нужное положение - им не хватает кинетической энергии для преодоления потенциального барьера. При этом система в целом находится в состоянии локального энергетического минимума. Для выхода из него металл нагревают до высокой температуре, а затем медленно охлаждают, позволяя атомам занять правильные положения в решетке, соответствующее глобальному минимуму энергии.
Субоптимальное решение некоторой задачи оптимизации, например, задачи коммивояжера, также может рассматриваться как решение в котором имеются дефекты - неправильные части маршрута. Лин и Кернигэн (Lin & Kernigan, 1973) ввели элементарные операции изменения текущего решения, такие как перенос (часть маршрута вырезается и вставляется в другое место) и обращение (выбирается фрагмент маршрута и порядок прохождения городов в нем меняется на обратный). При применении одной из этих операций происходит изменение маршрута с

на





Комбинаторная оптимизация и задача коммивояжера
В задачах комбинаторной оптимизации требуется найти наилучшее из конечного, но обычно очень большого числа возможных решений. Если задача характеризуется характерным числом элементов (размерностью задачи), то типичное число возможных решений, из которых предстоит сделать выбор, растет экспоненциально - как




Это свойство делает простой метод перебора всех вариантов, в принципе гарантирующий решение при конечном числе альтернатив, чрезвычайно неэффективным, т.к. такое решение требует экспоненциально большого времени. Эффективными же признаются решения, гарантирующие получение ответа за полиномиальное время, растущее как полином с ростом размерности задачи, т.е. как
N. 1)
Различие между полиномиальными и экспоненциальными алгоритмами восходит к фон Нейману (von Neumann, 1953)
Задачи, допускающие гарантированное нахождение оптимума целевой функции за полиномиальное время, образуют класс



Для более трудных задач достаточно было бы и более слабого условия - нахождения субоптимальных решений, локальных минимумов целевой функции, не слишком сильно отличающихся от абсолютного минимума. Нейросетевые решения как раз и представляют собой параллельные алгоритмы, быстро находящие субоптимальные решения оптимизационных задач, минимизируя целевую функцию в процессе своего функционирования или обучения.
Самые трудные задачи класса





Все

В классической постановке, коммивояжер должен объехать




Самые трудные задачи класса





Все

В классической постановке, коммивояжер должен объехать




Метод эластичной сети
Иной подход к решению задачи коммивояжера использовали в 1987 году Дурбин и Уиллшоу (Durbin & Willshaw, 1987). Хотя они явно и не использовали в своей работе понятия искусственной нейронной сети, но в качестве отправной точки упоминали об аналогии с механизмами установления упорядоченных нейронных связей. Исследователи предложили рассматривать каждый из маршрутов коммивояжера как отображение окружности на плоскость, так что в каждый город на плоскости отображается некоторая точка этой окружности. При этом требуется, чтобы соседние точки на окружности отображались в точки, по возможности ближайшие и на плоскости. Алгоритм стартует с помещения на плоскость небольшой окружности (кольца), которая неравномерно расширяясь проходит практически около всех городов и, в конечном итоге, определяет искомый маршрут. Каждая точка расширяющегося кольца движется под действием двух сил: первая перемещает ее в сторону ближайшего города, а вторая смещает в сторону ее соседей на кольце так, чтобы уменьшить его длину. По мере расширения такой эластичной сети, каждый город оказывается ассоциирован с определенным участком кольца.
Вначале все города оказывают приблизительно одинаковое влияние на каждую точку маршрута. В последующем, большие расстояния становятся менее влиятельными и каждый город становится более специфичным для ближайших к нему точек кольца. Такое постепенное увеличение специфичности, которое, конечно, напоминает уже знакомый нам метод обучения сети Кохонена, контролируется значением некоторого эффективного радиуса






где параметры








где




которая минимизируется в ходе динамического изменения параметров кольца.
Дурбин и Уиллшоу показали, что для задачи с 30 городами, рассмотренной Хопфилдом и Танком, метод эластичной сети генерирует наикратчайший маршрут примерно за 1000 итераций. Для 100 городов найденный этим методом маршрут лишь на 1% превосходил оптимальный.
Метод муравьиных колоний
Энтомологи установили, что муравьи способны быстро находить кратчайший путь от муравейника к источнику пищи. Более того, они могут адаптироваться к изменяющимся условиям , находя новый кратчайший путь. Рассмотрим рисунок 6.5: муравьи движутся по прямой, соединяющей муравейник с местом, в котором находится пища. При движении муравей метит свой путь специальными веществами - феромонами, и эта информация используется другими муравьями для выбора пути. А именно, муравьи предпочитают тропки наиболее обогащенные феромонами. Это элементарное правило поведения муравьев и определяет их способность находить новые пути, если старый оказывается перерезанным преградой. Действительно, достигнув этой преграды, муравьи уже не смогут продолжить свой путь и с равной вероятностью будут обходить ее справа и слева. То же самое будет происходить и на обратной стороне преграды. Однако, те муравьи, которые случайно выберут кратчайший путь (налево от преграды и направо - на обратном пути), будут быстрее проходить свой путь и он с большей скоростью станет обогащаться феромонами. Поэтому следующие муравьи будут предпочитать именно этот наикратчайший путь, метя его и далее. Очевидная положительная обратная связь быстро приведет к тому, что кратчайший путь станет единственным маршрутом движения насекомых.
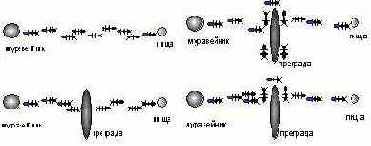
Рис. 6.5. Муравьи находят новый кратчайший новый путь (сверху от преграды) который быстрее обогащается феромонами
Подобный процесс может осуществляться и в компьютерном мире, населенном Искусственными Муравьями (ИМ). Такие муравьи могут решить и нашу задачу коммивояжера. В этом случае они движутся от города к городу по ребрам соответствующего графа. При этом они выбирают направление движения, используя вероятностную функцию, зависящую как от предыдущих попыток движения по данному ребру, так и от эвристического значения, являющегося функцией длины ребра. ИМ с большей вероятностью будут предпочитать ближайшие города и города, связанные ребрами, наиболее богатыми феромонами.
Первоначально искусственных муравьев размещаются в случайно выбранных городах. В каждый последующий момент времени они перемещаются в соседние города и изменяют концентрацию феромона на своем пути (локальная модификация). После того, как все ИМ завершат движения по замкнутому маршруту, тот из них, который проделал кратчайший путь, добавляет к его звеньям количество феромона, обратно пропорциональное длине этого пути (глобальная модификация). В отличие от живых муравьев, ИМ обладают способностью определять расстояние до соседних городов и помнят, какие города они уже посетили. Оказывается, метод искусственных муравьиных колоний может давать результаты, лучшие чем при использовании имитации отжига, нейронных сетей, и генетических алгоритмов.
| 1 | 5.86 | 5.88 | 5.98 | 6.06 |
| 2 | 6.05 | 6.01 | 6.03 | 6.25 |
| 3 | 5.57 | 5.65 | 5.70 | 5.83 |
| 4 | 5.70 | 5.81 | 5.86 | 5.87 |
| 5 | 6.17 | 6.33 | 6.49 | 6.70 |
Напомним вновь, что при электронной или оптической реализации нейросетевой подход находится вне конкуренции в ситуациях, когда необходимо очень быстро находить не обязательно оптимальное, но достаточно хорошее решение.
Нейросетевая оптимизация и другие "биологические "методы
Преимущества и недостатки нейросетевой оптимизации познаются в сравнении с другими развитыми в настоящее время методами. Из методов, которые иногда дают аналогичные, а порой и лучшие результаты, отметим генетические и эволюционные алгоритмы (Fogel, 1993), а также метод муравьиных колоний (Dorigo & Gambardella, 1996).
В этом разделе мы очень кратко остановимся на них, поскольку эти подходы, так же как и нейросети, используют ясные и плодотворные биологические аналогии. Кроме того, генетические алгоритмы широко используются и для обучения нейронных сетей самих по себе, поскольку обучение нейросетей связано с минимизацией функционала ошибки.
Оптимизация и сеть Хопфилда
В 1985г. Хопфилд и Танк предложили использовать минимизирующие энергию нейронные сети для решения задач оптимизации (Hopfield & Tank, 1985). В качестве примера они, естественно, рассмотрели задачу коммивояжера.
Для решения этой задачи с помощью нейронной сети Хопфилда нужно закодировать маршрут активностью нейронов и так подобрать связи между ними, чтобы энергия сети оказалась связанной с полной длиной маршрута. Хопфилд и Танк предложили для этого следующий способ.
Рассмотрим сеть, состоящую из










и

первое из которых говорит о том, что любой город в маршруте встречается лишь однажды, а второе - что маршрут проходит через каждый город.
Общий подход к ограничениям в задачах оптимизации состоит в том, что в итоговый функционал, подлежащий минимизации, включаются штрафные члены, увеличивающие целевую функцию при отклонении от накладываемых ограничений. В данном случае в качестве энергии состояния сети можно выбрать функционал

где т.н. множитель Лагранжа

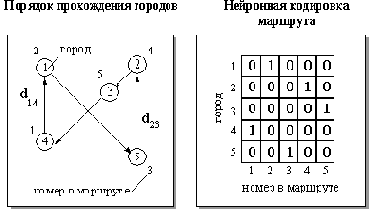
Рис. 6.1. Слева - один из возможных маршрутов коммивояжера в случае задачи с 5 городами. Справа - кодировка этого маршрута состояниями 25 бинарных нейронов
Осмысленному решению будет соответствовать стационарное состояние сети, в котором лишь



Величина множителя Лагранжа


Наоборот, длина маршрута может быть достаточно мала, но одно из оставшихся слагаемых будет ненулевым и маршрут окажется не интерпретируем или недостаточен (например, проходит не через все города).
После того, как минимизируемая целевая функция для задачи коммивояжера построена, можно определить, какие связи в нейронной сети Хопфилда следует выбрать, так чтобы функционал энергии состояния в ней совпал с этой функцией. Для этого достаточно приравнять выражение для


Таким образом находятся значения синаптических связей в сети:

и значений порогов нейронов


Сети Поттса. Значительного продвижения в эффективности нейросетевой оптимизации можно добиться выбрав более сложный тип нейронов - т.н. Поттсовские нейронны - для более естественного представления условий задачи в терминах нейросети (Gilsen et al., 1989). Поттсовский нейроны принимают одно из N значений, что можно описать N-вектором

После того как сеть построена, можно, стартуя со случайного начального состояния, проследить ее эволюцию к стационарной конфигурации, которая может дать если не оптимальное, то по крайней мере хорошее решение задачи. К сожалению, в описанном виде сеть чаще всего "застревает" в локальном минимуме относительно далеком от оптимума.
Для улучшения ситуации Хопфилд и Танк предложили использовать сети с непрерывными (аналоговыми) нейронами, принимающими любые значения в интервале

. 1) В качестве тестовых они использовали задачи с 10 и 30 городами. В первом случае сеть в 20 попытках 16 раз эволюционировала к состояниям, описывающим осмысленный маршрут и в 10 случаях давала один из двух возможных оптимальных маршрутов. Поскольку для задачи с



Таким образом, выигрыш при использовании сети, по сравнению со случайным выбором составляет



В дальнейшем разные исследователи выявили и другие особенности описанного подхода. Было показано, что недостатком оригинальной схемы Хопфилда и Танка является то, что простейшая сеть Хопфилда имеет тенденцию включать в маршрут ближайшие друг к другу города. Это происходит из-за того, что в определяющую длину маршрута часть функции Ляпунова входят парные произведения состояний нейронов сети. В результате, с увеличением числа городов маршрут, предлагаемый сетью, как правило, распадается на локально оптимальные участки, соединение которых, однако, далеко от оптимального. Ситуацию можно улучшить, если стимулировать сеть находить, например, локально наилучшие тройки городов. Для этого основная часть функции Ляпунова может быть представлена в виде

Однако, сети, динамика которых направляется такой функцией Ляпунова, должны состоять из более сложных нейронов, нелинейно суммирующих внешние воздействия - нейронов высокого порядка ( в данном случае - второго):

Купер показал, что использование таких сетей значительно улучшает результаты поиска оптимального решения. Так для

Отметим в заключение, что мы упомянули только о небольшой части разработанных к настоящему времени способов улучшения свойств минимизирующих энергию нейронных сетей при решения задач оптимизации.
Оптимизация с помощью сети Кохонена.
Успех применения метода эластичной сети для решении задачи коммивояжера был оценен Фаватой и Уолкером, понявшими, что в нем, по сути, используется отображение двумерного распределения городов на одномерный кольцевого маршрута (Favata & Walker, 1991). Поскольку в наиболее общем виде такой подход был сформулирован Кохоненом, то использование его самоорганизующихся карт для оптимизации оказалось вполне естественным. Сеть Кохонена позволяет обеспечить выполнение условия, которому должен удовлетворять хороший маршрут в задаче коммивояжера: близкие города на плоскости должны быть отображены на близкие в одномерном маршруте.
Алгоритм решения задачи следует из оригинальной схемы Кохонена, в которую вносятся лишь небольшие изменения. Используется сеть, состоящая из двух одномерных слоев нейронов (т.е. содержащая лишь один слой синаптических весов). Входной слой состоит из трех нейронов, а выходной - из N (по числу городов). Каждый нейрон входного слоя связан с каждым выходным нейроном. Все связи вначале инициируются случайными значениями. Для каждого города входной 3-мерный вектор формируется из двух его координат на плоскости, а третья компонента вектора представляет из себя нормирующий параметр, вычисляемый так, чтобы все входные вектора имели одинаковую Евклидову длину и никакие два вектора не были бы коллинеарны. Это эквивалентно рассмотрению двумерных координат городов, как проекций трехмерных векторов, лежащих на сфере. Обозначим через





Алгоритм формирования маршрута формулируется следующим образом. Выбираются значения для параметра усиления


Выбирается случайный город










Для устранения концевых эффектов слой выходных нейронов считается кольцевым, так что N-й нейрон примыкает к первому. Радиус взаимодействия постепенно уменьшается согласно некоторому правилу (например, вначале можно положить


Конкретный вид законов изменения радиуса взаимодействия и параметра усиления, как правило, не имеет большого значения.
После завершения процесса обучения, положение города в маршруте определится положением его образа в кольцевом выходном слое. Иногда случается, что два или большее число городов отображаются на один и тот же выходной нейрон. Подобная ситуация может интерпретироваться так, что локальное упорядочивание этих городов не имеет значения и требует только локальной оптимизации части маршрута. При нескольких десятках городов такая оптимизация может скорректировать его длину на величину до 25%. Для сотен городов она, как правило, не улучшает результат и поэтому не используется.
Эксперименты Фаваты и Уолкера, проведенные для задачи коммивояжера с 30 городами дали лучшие результаты, чем полученные с помощью сети Хопфилда (см. таблицу).
| Длина маршрута | <7 | <5.73 |
| Средняя длина маршрута | >6 | 4.77 |
| Наименьшая длина маршрута | 5.07 | 4.26 |
Однако для большего числа городов сеть Кохонена все же в среднем дает более длинные маршруты, чем метод имитации отжига (примерно на 5%). При практическом применении нейросетевых подходов к решению задач оптимизации, однако, главное значение имеет не столько близость решения к глобальному оптимуму, сколько эффективность его получения. В этом смысле сеть Кохонена значительно эффективнее имитации отжига. Однако, и ее использование, как и в случае использования других лучших методов оптимизации, требует вычислительных затрат, растущих не медленне, чем

Растущие нейронные сети
Эффективное практическое применение нейронных сетей для оптимизации возможно, если вычислительные затраты у соответствующей модели не слишком быстро растут с ростом размерности задачи. Так, для задачи коммивояжера затраты при эмуляции сети Хопфилда на последовательном компьютере растут как



весов. 1)
Эвристический подход Лина и Кернигана масштабирует вычислительные затраты как

Предложенная ими модель относится к классу растущих нейронных сетей. Такие сети по-своему решают задачу адаптации своей структуры к требованиям решаемой задачи. Вспомним многослойные персептроны, для которых количества скрытых слоев и нейронов в них часто выбираются методом проб и ошибок. Как уже отмечалось в связи с этим, имеются два подхода к адаптивному выбору архитектуры нейросетей. В первом подходе заведомо избыточная нейросеть прореживается до нужной степени сложности. Растущие сети, напротив, стартуют с очень простых и небольших структур, которые разрастаются и усложняются по мере необходимости.
Фритцке и Вильке разработали целый класс самоорганизующихся (и обучаемых с учителем) сетей с изменяющейся структурой, такие как Растущие Клеточные Структуры, Растущий Нейронный Газ и Растущие Сетки. Первые и были использованы ими для решения задачи коммивояжера (и других задач комбинаторной оптимизации).
Растущая клеточная структура для задачи коммивояжера представляет из себя вначале кольцо из трех ячеек нейронов. Каждый нейрон характеризуется двумерным вектором


Смещение (см. рисунок 6.2)
выбирается случайный город




Эти операции очень близки к используемым в модели Кохонена. Различие состоит в том, что в последней радиус, в котором определяется соседство и параметр адаптации уменьшаются со временем.
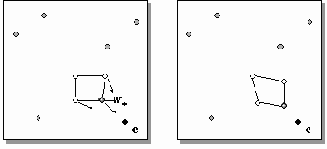
Рис. 6.2. Процедура смещения перемещает нейрон-победитель и его ближайших соседей в сторону случайно выбранного города
