Архитектура связей

На способ обработки информации решающим образом сказывается наличие или отсутствие в сети петель обратных связей. Если обратные связи между нейронами отсутствуют (т.е. сеть имеет структуру последовательных слоев, где каждый нейрон получает информацию только с предыдущих слоев), обработка информации в сети однонаправленна. Входной сигнал обрабатывается последовательностью слоев и ответ гарантированно получается через число тактов равное числу слоев.

Наличие же обратных связей может сделать динамику нейросети (называемой в этом случае рекуррентной) непредсказуемой. В принципе, сеть может "зациклиться" и не выдать ответа никогда. Причем, согласно Тьюрингу, не существует алгоритма, позволяющего для произвольной сети определить придут ли когда-либо ее элементы в состояние равновесия (т.н. проблема останова).

Вообще говоря, то, что нейроны в рекуррентных сетях по многу раз принимают участие в обработке информации позволяет таким сетям производить более разнообразную и глубокую обработку информации. Но в этом случае следует принимать специальные меры к тому, чтобы сеть не зацикливалась (например, использовать симметричные связи, как в сети Хопфилда, или принудительно ограничивать число итераций, как это делается в эмуляторе MultiNeuron группы НейроКомп).

Таблица 2.6. Сравнение архитектур связей нейросетей

Сравнение сетей:Без обратных связей (многослойные)С обратными связями

Преимущества	Простота реализации. Гарантированное получение ответа после прохождения данных по слоям.	Минимизация размеров сети - нейроны многократно участвуют в обработке данных. Меньший объем сети облегчает процесс обучения.
Недостатки	Требуется большее число нейронов для алгоритмов одного и того же уровня сложности. Следствие - большая сложность обучения.	Требуются специальные условия, гарантирующие сходимость вычислений.

Что такое парадигмы

Парадигмы нейрокомпьютинга - это родовые черты, объединяющие принципы работы и обучения всех нейрокомпьютеров. Главное, что их объединяет - нацеленность на обработку образов. Эта их особенность, аналогичная способу функционирования мозга, уже обсуждалась ранее во вводной лекции. Теперь же мы сформулируем эти парадигмы в концентрированном виде безотносительно к биологическим прототипам, как способы обработки данных. Эти общие сведения послужат фундаментом для более подробного разбора отдельных нейро-архитектур в последующих лекциях.

Где применяются нейросети

Наверное, в каждой предметной области при ближайшем расмотрении можно найти постановки нейросетевых задач. Список областей, где решение такого рода задач имеет практическое значение уже сейчас, приведенный ниже, ограничен лишь опасением утомить читателя. По этой же причине мы ограничились единственным примером конкретного применения в каждой из этих областей.

Экономика и бизнес: предсказание рынков, автоматический дилинг, оценка риска невозврата кредитов, предсказание банкротств, оценка стоимости недвижимости, выявление пере- и недооцененных компаний, автоматическое рейтингование, оптимизация портфелей, оптимизация товарных и денежных потоков, автоматическое считывание чеков и форм, безопасность транзакций по пластиковым карточкам. Программное обеспечение компании RETEK, дочерней фирмы HNC Software, - лидер среди крупных ритейлоров с оборотом свыше $1 млрд. Ее последний продукт января 1998 года Retek Predictive Enterprise Solution включает развитые средства нейросетевого анализа больших потоков данных, характерных для крупной розничной торговли. Он также содержит прогнозный блок, чтобы можно было заранее просчитать последствия тех или иных решений. (http://www.retek.com)

Медицина: обработка медицинских изображений, мониторинг состояния пациентов, диагностика, факторный анализ эффективности лечения, очистка показаний приборов от шумов. Группа НейроКомп из Красноярска (под руководством Александра Николаевича Горбаня) совместно с Красноярским межобластном офтальмологическом центром им. Макарова разработали систему ранней диагностики меланомы сосудистой оболочки глаза. Этот вид рака составляют почти 90% всех внутриглазных опухолей и легко диагностируется лишь на поздней стадии. Метод основан на косвенном измерении содержания меланина в ресницах. Полученные данные спектрофотометрии, а также общие характеристики обследуемого (пол, возраст и др.) подаются на входные синапсы 43-нейронного классификатора. Нейросеть решает, имеется ли у пациента опухоль, и если да, то определяет ее стадию, выдавая, кроме этого, процентную вероятность своей уверенности (http://www.chat.ru/~neurocom/).

Авионика: обучаемые автопилоты, распознавание сигналов радаров, адаптивное пилотирование сильно поврежденного самолета. Компания McDonnell Douglas Electronic Systems разработала автоматический переключатель режимов полета в реальном масштабе времени в зависимости от вида повреждения самолета. Данные от 20 сенсорных датчиков и сигналов от пилота используются нейросетью для выработки около 100 аэродинамических параметров полета. Сильной стороной является возможность сети адаптироваться к непредсказуемым аэродинамическим режимам, таким как потеря части крыла и т.д. (SIGNAL Magazin, февраль 1991)

Связь: сжатие видео-информации, быстрое кодирование-декодирование, оптимизация сотовых сетей и схем маршрутизации пакетов. Нейросети уже продемонстрировали коэффициент сжатия 120:1 для черно-белого видео. Цветное видео допускает примерно вдвое большую степень сжатия 240:1 за счет специальной схемы кодирования цветов. (http://www.ee.duke.edu/~cec/JPL/paper.html)

Интернет: ассоциативный поиск информации, электронные секретари и агенты пользователя в сети, фильтрация информации в push-системах, коллаборативная фильтрация, рубрикация новостных лент, адресная реклама, адресный маркетинг для электронной торговли. Фирма Autonomy отделилась от родительской фирмы Neurodynamics в июне 1996 года с уставным капиталом $45 млн и идеей продвижения на рынок Internet электронных нейросетевых агентов. Согласно ее пресс-релизу, первоначальные вложения окупились уже через год. Компания производит семейство продуктов AGENTWARE, создающих и использующих профили интересов пользователей в виде персональных автономных нейро-агентов. Такие компактные нейро-агенты (< 1 Кб) могут представлять пользователя в любом из продуктов компании. Например, агенты могут служить в качестве нейро-секретарей, фильтруя поступающую по информационным каналам информацию. Они также могут постоянно находиться на сервере провайдера, или посылаться для поиска в удаленных базах данных, осуществляя отбор данных на месте.


В будущем, когда эта технология получит достаточное распространение, она позволит снизить нагрузку на трафик Сети. (http://www.agentware.com)

Автоматизация производства: оптимизация режимов производственного процесса, комплексная диагностика качества продукции (ультразвук, оптика, гамма-излучение, …), мониторинг и визуализация многомерной диспетчерской информации, предупреждение аварийных ситуаций, робототехника. Ford Motors Company внедрила у себя нейросистему для диагностики двигателей после неудачных попыток построить экспертную систему, т.к. хотя опытный механик и может диагностировать неисправности он не в состоянии описать алгоритм такого распознавания. На вход нейро-системы подаются данные от 31 датчика. Нейросеть обучалась различным видам неисправностей по 868 примерам.



После полного цикла обучения качество диагностирования неисправностей сетью достигло уровня наших лучших экспертов, и значительно превосходило их в скорости. Marko K, et. al. , Ford Motors Company, Automative Control Systems Diagnostics, IJCNN 1989

Политические технологии: анализ и обобщение социологических опросов, предсказание динамики рейтингов, выявление значимых факторов, объективная кластеризация электората, визуализация социальной динамики населения. Уже упоминавшаяся ранее группа НейроКомп из Красноярска довольно уверенно предсказывает результаты президентских выборов в США на основании анкеты из 12 вопросов. Причем, анализ обученной нейросети позволил выявить пять ключевых вопросов, ответы на которых формируют два главных фактора, определяющих успех президентской кампании. Этот пример будет рассмотрен более подробно в лекции, посвященной извлечению знаний с помощью нейросетей.

Безопасность и охранные системы: системы идентификации личности, распознавание голоса, лиц в толпе, распознавание автомобильных номеров, анализ аэро-космических снимков, мониторинг информационных потоков, обнаружение подделок. Многие банки используют нейросети для обнаружения подделок чеков. Корпорация Nestor (Providence, Rhode Island) установила подобную систему в Mellon Bank, что по оценкам должно сэкономить последнему $500,000 в год.


Нейросеть обнаруживает в 20 раз больше подделок, чем установленная до нее экспертная система. (Tearing up the Rules, Banking Technology, ноябрь 1993)

Ввод и обработка информации: Обработка рукописных чеков, распознавание подписей, отпечатков пальцев и голоса. Ввод в компьютер финансовых и налоговых документов. Разработанные итальянской фирмой RES Informatica нейросетевые пакеты серии FlexRead, используются для распознавания и автоматического ввода рукописных платежных документов и налоговых деклараций. В первом случае они применяются для распознавания не только количества товаров и их стоимости, но также и формата документа. В случае налоговых деклараций распознаются фискальные коды и суммы налогов.

Геологоразведка: анализ сейсмических данных, ассоциативные методики поиска полезных ископаемых, оценка ресурсов месторождений. Нейросети используются фирмой Amoco для выделения характерных пиков в показаниях сейсмических датчиков. Надежность распознавания пиков - 95% по каждой сейсмо-линии. По сравнению с ручной обработкой скорость анализа данных увеличилась в 8 раз. (J.Veezhinathan & D.Wadner, Amoco, First Break Picking, IJCNN, 1990)



Обилие приведенных выше применений нейросетей - не рекламный трюк. Просто нейросети - это не что иное, как новый инструмент анализа данных. И лучше других им может воспользоваться именно специалист в своей предметной области. Основные трудности на пути еще более широкого распространения нейротехнологий - в неумении широкого круга профессионалов формулировать свои проблемы в терминах, допускающих простое нейросетевое решение. Данный курс призван как раз помочь усвоить типовые постановки задач для нейросетей. Для этого, прежде всего, нужно четко представлять себе основные особенности нейросетевой обработки информации - парадигмы нейрокомпьютинга.

Готовые нейро-пакеты

Это законченные независимые программные продукты, предназначенные для широкого класса задач, в основном - для предсказаний и статистической обработки данных. Большинство из имеющихся на рынке нейропакетов имеет дружественный интерфейс пользователя, не требующий знакомства с языками программирования.

Множество нейро-эмуляторов начального уровня можно найти в Internet как shareware или freeware. Это, обычно, многослойные персептроны с одним или несколькими правилами обучения. Исключение составляет вполне профессиональный Штутгартский симулятор с большим набором возможностей, работающий, правда, только на UNIX-машинах. Коммерческие пакеты отличаются от свободно распространяемых большим набором средств импорта и предобработки данных, дополнительными возможностями по анализу значимости входов и оптимизации структуры сети. Стоимость коммерческих эмуляторов - масштаба $1000. Как правило, такие пакеты (BrainMaker Professional, NeuroForecaster, Лора-IQ300) имеют собственный встроенный блок предобработки данных, хотя иногда для этой цели удобнее использовать стандартные электронные таблицы. Так, нейро-продукты группы нейрокомпьютинга ФИАН встраивается непосредственно в Microsoft Excel в качестве специализированных функций обработки данных. При этом всю предобработку данных и визуализацию результатов можно проводить стандартными средствами Excel, который, кроме того, имеет богатый и расширяемый набор конверторов для импорта и экспорта данных.

Такие пакеты нацелены на решение информационных задач в диалоговом режиме - при непосредственном участии пользователя. Они не применимы в условиях потоковой обработки данных. Кроме того, они не приспособлены для разработки сложных систем обработки данных, состоящих из многих блоков, содержащих, скажем, сотни нейросетей, адаптивно настраивающихся и дообучающихся на вновь поступающих данных. Разработка таких "серьезных" систем требует специального инструментария.

Готовые решения на основе нейросетей

Это - конечный результат. Здесь нейросети спрятаны от пользователя в недрах готовых автоматизированных комплексов, предназначенных для решения конкретных производственных задач. Например, уже упоминавшийся продукт Falcon встраивается в банковскую автоматизированную систему обслуживания платежей по пластиковым карточкам. В другом случае это будет автоматизированная система управления заводом или реактором. Конечного пользователя, как правило, не интересует способ достижения результата, ему важно лишь качество продукта. Поскольку многие такие готовые решения обладают уникальными возможностями (пока специалисты по нейрокомпьютингу еще в дефиците) и обеспечивают реальные конкурентные преимущества, их цена может быть довольно высока - порядка $106 - гораздо выше, чем стоимость нейро-hardware.

Испанская компания SEMP занимается повышением эффективности обслуживания кредитных карт VISA, эмитируемых испанскими банками. Количество подобных транзакций - от 500,000 до 1,000,000 в день. Нейросетевая система, разработанная для нее учеными из Мадридского Института Инженерии Знаний (Instituto de Ingenieria del Conocimiento), уменьшила вероятность несанкционированного использования карт на 30-40% для основных каналов мошенничества.

Инструменты разработки нейроприложений

Главное, что отличает этот класс программного обеспечения - способность генерировать "отчуждаемые" нейросетевые продукты, т.е. генерировать программный код, использующий обученные нейросети для обработки данных. Такой код может быть встроен в качестве подсистемы в любые сколь угодно сложные информационные комплексы.

Примерами подобных систем, способных генерировать исходные тексты программ являются NeuralWorks Professional II Plus (стоимостью от $3000) фирмы NeuralWare и отечественный Neural Bench (нейро-верстак). Последний интересен, кроме прочего, тем, что может генерировать коды на многих языках, включая Java. Такие Java-апплеты могут использоваться для организация различного рода сервисов в глобальных и локальных сетях. Удобным инструментом разработки сложных нейросистем является MATLAB с прилагающимся к нему нейросетевым инструментарием, органично вписавшимся в матричную идеологию этой системы. MATLAB предоставляет удобную среду для синтеза нейросетевых методик с прочими методами обработки данных (wavelet-анализ, статистика, финансовый анализ и т.д.). Разработанные в системе MATLAB приложения могут быть затем перетранслированы в C++.

Подобные средства разработки используются фирмами, в частности, для создания основанных на нейросетевой обработке данных готовых решений в различных областях.

Элементная база нейрокомпьютеров

Практически все действующие нейрокомпьютеры используют традиционную элементную базу: микроэлектронные СБИС. Сотни миллиардов долларов, уже вложенные в развитие этой технологии, дают ей решающее преимущество перед другими альтернативами, такими, как оптические вычисления.

Современная электроника опирается, в основном, на цифровую обработку сигналов, устойчивую к помехам и технологическим отклонениям в параметрах базовых злементов. Цифровая схемотехника предоставляет нейро-конструкторам наиболее богатый инструментарий. Поэтому неудивительно, что наибольшее распространение получили именно цифровые нейрокомпьютеры. Это по существу - специализированные матричные ускорители, использующие матричный, послойный характер обработки сигналов в нейросетях. Широко используются стандартные процессоры обработки сигналов (DSP - Digital Signal Processors), оптимизированные под такие операции.

Примером современного DSP-процессора, приспособленного для ускорения нейро-вычислений является продукт Texas Instruments TMS320C80 производительностью 2 млрд. операций в секунду. Этот кристалл включает пять процессоров и реализует сразу две технологии - DSP и RISK (4 32-разрядных сигнальных процессора с фиксированной точкой и управляющий процессор с плавающей арифметикой).

Однако, сама природа нейросетевой обработки информации - аналоговая, и дополнительного выигрыша в скорости вычислений (по некоторым оценкам ~103-104) и плотности вычислительных элементов можно добиться, используя специализированную аналоговую элементную базу (Mead, 1989). Наиболее перспективны, по-видимому аналоговые микросхемы с локальными связями между элементами (т.н. клеточные нейросети, CNN - Cellular Neural Networks), например силиконовая ретина фирмы Synaptics. С другой стороны, разработка аналоговых чипов с использованием нетрадиционных схемотехнических решений требует дополнительных и немалых затрат. В настоящее время эти работы на Западе развернуты широким фронтом, например, в рамках проекта SCX-1 (Silicon Cortex - кремниевая кора).
Этот проект отличает принципиальная ориентация на массовых производителей аппаратуры, обеспечиваемая совместимостью разрабатываемых нейроплат со стандартами шины VME. Вот как оценивает перспективы этих разработок один из пионеров российского нейрокомпьютинга Феликс Владимирович Широков:

Системы промышленной автоматизации, построенные на VME, обретут нейроморфный мозг, способность видеть и слышать, ощущать электрические и магнитные поля, воспринимать ультразвуки и радиацию. Они смогут анализировать обстановку и принимать решения. Это будет прививкой разума системам промышленной автоматизации. Широков, 1998

Преимущества обоих подходов пытаются совместить гибридные микросхемы, имеющие цифровой интерфейс с остальной аппаратурой, но исполняющие наиболее массовые операции аналоговым способом.

Приведенные ниже таблицы (таблица 2.1 и Таблица 2.2 ) дают некоторое представление о сильных и слабых сторонах различных элементных баз и достигнутых результатах.

Таблица 2.1. Сравнение типов элементной базыТип элементной базыПреимущества Недостатки

Аналоговая оптическая	Допускает массовые межсоединения	Нет замкнутой технологии оптических вычислений
Аналоговая электрическая	Концептуальная простота схемотехники, выигрыш в емкости схем и скорости вычислений	Жесткие технологические требования, чувствительность к дефектам и внешним воздействиям, малая точность вычислений, трудность реализации массовых соединений
Цифровая электрическая	Развитая замкнутая технология, точность вычислений, устойчивость к технологическим вариациям	Сложность схемных решений, многотактовое выполнение базовых операций, трудность реализации массовых соединений
Гибридная (аналого-цифровая схемотехника, оптоэлектроника)	Аналоговое ускорение базовых операций при цифровом интерфейсе с внешними устройствами, возможности оптической коммутации	Требует дополнительных технологических разработок

Таблица 2.2. Сравнительные характеристики некоторых нейросхемНазвание нейросхемы (фирма-производитель)Тип элементной базы Емкость (кол-во нейронов / кол-во синапсов)Производительность (кол-во умножений с сумированием в сек)

Silicon Retina (Synaptics)	Аналоговая		?
ETANN (Intel)	Аналоговая
N64000 (Inova)	Цифровая
MA-16 (Siemens)	Цифровая
RN-200 (Ricoh)	Гибридная
NeuroClassifier (Mesa Research Institute)	Гибридная

Как устроены нейрокомпьютеры

Преимущества нейрокомпьютинга состоит в возможности организовать массовые параллельные вычисления. Поэтому базовые процессорные элементы обычно соединяют в вычислительные комплексы: как можно больше - на одном чипе, а что не поместилось - в мультипроцессорные платы.

Эти платы затем либо вставляют в персональные компьютеры и рабочие станции в качестве нейро-ускорителей, либо собирают в полномасштабные нейрокомпьютеры. В последнем случае избегают задержек в относительно медленных системных шинах PC, правда ценой удорожания аппаратуры.

Таблица 2.3. Сравнительные характеристики некоторых нейрокомпьютеров

Название нейросхемы, фирма-производительТипКоличество процессорных элементовПроизводительность (кол-во умножений с суммированием в сек)

CNAPS/PC (Adaptive Solutions)	PC-ускоритель	2 CNAPS-1016 процессора (128 нейронов)
CNAPS (Adaptive Solutions)	Нейрокомпьютер	8 CNAPS-1016 процессоров (512 нейронов)
SYNAPSE-1 (Siemens)	Нейрокомпьютер	8 MA-16 процессоров (512 нейронов)

Какие задачи решают нейросети

Нейросети наиболее приспособлены к решению широкого круга задач, так или иначе связанных с обработкой образов. Вот список типичных постановок задач для нейросетей:

Аппроксимация функций по набору точек (регрессия) Классификация данных по заданному набору классов Кластеризация данных с выявлением заранее неизвестных классов-прототипов Сжатие информации Восстановление утраченных данных Ассоциативная память Оптимизация, оптимальное управление

Этот список можно было бы продолжить и дальше. Заметим, однако, что между всеми этими внешне различными постановками задач существует глубокое родство. За ними просматривается некий единый прототип, позволяющий при известной доле воображения сводить их друг к другу.

Возьмем, например, задачу аппроксимации функции по набору точек. Это типичный пример некорректной задачи, т.е. задачи не имеющей единственного решения. Чтобы добиться единственности, такие задачи надо регуляризировать - дополнить требованием минимизации некоторого регуляризирующего функционала. Минимизация такого функционала и является целью обучения нейросети. Задачи оптимизации также сводятся к минимизации целевых функций при заданном наборе ограничений. С другой стороны, классификация - это ни что иное, как аппроксимация функции с дискретными значениями (идентификаторами классов), хотя ее можно рассматривать и как частный случай заполнения пропусков в базах данных, в данном случае - в колонке идентификаторов класса. Задача восстановления утраченных данных, в свою очередь - это ассоциативная память, восстанавливающая прообраз по его части. Такими прообразами в задаче кластеризации выступают центры кластеров. Наконец, если информацию удается восстановить по какой-нибудь ее части, значит мы добились сжатия этой информации, и т.д.

Многие представители разных наук, занимающихся перечисленными выше задачами и уже накопившими изрядный опыт их решения, видят в нейросетях лишь перепев уже известных им мотивов. Каждый полагает, что перевод его методов на новый язык нейросетевых схем ничего принципиально нового не дает. Статистики говорят, что нейросети - это всего лишь частный способ статистической обработки данных, специалисты по оптимизации - что методы обучения нейросетей давно известны в их области, теория аппроксимации функций рассматривает нейросети наряду с другими методами многомерной аппроксимации. Нам же представляется, что именно синтез различных методов и идей в едином нейросетевом подходе и является неоценимым достоинством нейрокомпьютинга. Нейрокомпьютинг предоставляет единую методологию решения очень широкого круга практически интересных задач. Это, как правило, ускоряет и удешевляет разработку приложений. Причем, что обычно забывают за неразвитостью соответствующего hardware, но что, видимо, в конце концов сыграет решающую роль, нейросетевые алгоритмы решения всех перечисленных выше задач заведомо параллельны. Следовательно, все что может быть решено - может быть при желании решено гораздо быстрее и дешевле.

Классификация по типу связей и типу обучения (Encoding-Decoding)

Ограничившись лишь двумя описанными выше факторами, разделяющими сети по типу обучения (программирования) и функционирования, получим следующую полезную классификацию базовых нейро-архитектур, впервые предложенную, по-видимому, Бартом Коско (Таблица 2.7).

Таблица 2.7. Классификация нейросетей

Тиб обучения (Coding) Тип связей (Decoding) С "учителем"Без "учителя"

Без обратных связей	Многослойные персептроны (аппроксимация функций, классификация)	Соревновательные сети, карты Кохонена (сжатие данных, выделение признаков)
С обратными связями	Рекуррентные аппроксиматоры (предсказание временных рядов, обучение в режиме on-line)	Сеть Хопфилда (ассоциативная память, кластеризация данных, оптимизация)

В этой таблице различные архитектуры сетей, которые встретятся нам далее в этой книге, распределены по ячейкам в зависимости от способа обработки ими информации и способа их обучения. В скобках указаны основные типы задач, обычно решаемых данным классом нейросетей.

В следующих лекциях, после более близкого знакомства с перечисленными выше основными нейро-архитектурами, мы рассмотрим конкретные примеры задач из области финансов и бизнеса, интересные с практической точки зрения.

Коннекционизм

Отличительной чертой нейросетей является глобальность связей. Базовые элементы искусственных нейросетей - формальные нейроны - изначально нацелены на работу с широкополосной информацией. Каждый нейрон нейросети, как правило, связан со всеми нейронами предыдущего слоя обработки данных (см. рисунок 2.3, иллюстрирующий наиболее широко распространенную в современных приложениях архитектуру многослойного персептрона). В этом основное отличие формальных нейронов от базовых элементов последовательных ЭВМ - логических вентилей, имеющих лишь два входа. В итоге, универсальные процессоры имеют сложную архитектуру, основанную на иерархии модулей, каждый из которых выполняет строго определенную функцию. Напротив, архитектура нейросетей проста и универсальна. Специализация связей возникает на этапе их обучения под влиянием конкретных данных.

Рис. 2.3.  Глобальность связей в искуственных нейросетях

Типичный формальный нейрон производит простейшую операцию - взвешивает значения своих входов со своими же локально хранимыми весами и производит над их суммой нелинейное преобразование:

Рис. 2.4.  Нейрон производит нелинейную операцию над линейной комбинацией входов

Нелинейность выходной функции активации

принципиальна. Если бы нейроны были линейными элементами, то любая последовательность нейронов также производила бы линейное преобразование, и вся нейросеть была бы эквивалентна одному нейрону (или одному слою нейронов - в случае нескольких выходов). Нелинейность разрушает линейную суперпозицию и приводит к тому, что возможности нейросети существенно выше возможностей отдельных нейронов.

Краткая история нейрокомпьютинга

В прошлой лекции появление нейрокомпьютеров представлено как закономерный этап развития вычислительной техники. В результате, у читателя может сложиться впечатление, что и сама идея нейрокомпьютинга - недавнее изобретение. Это, однако, не так. Пути Эволюции редко бывают прямыми. Идеи нейрокомпьютинга появились практически одновременно с зарождением последовательных ЭВМ.

Ключевая работа Мак Каллока и Питтса по нейро-вычислениям (McCulloch and Pitts, 1943) появилась в 1943 году, на два года раньше знаменитой докладной записки фон Неймана о принципах организации вычислений в последовательных универсальных ЭВМ.

Однако, должны были пройти многие десятилетия, прежде чем радикальное удешевление аппаратуры позволило им заявить о себе в полный голос. Дело в том, что последовательная архитектура обладает весьма ценным преимуществом перед параллельной, решающим на ранних стадиях развития вычислительной техники. А именно, она позволяет получать полезные результаты уже при минимальном количестве аппаратуры. В следующей лекции мы покажем, что обучение нейросетей требует больших вычислительных затрат (сложность обучения растет как третья степень размерности задачи). Поэтому нейрокомпьютинг предъявляет достаточно жесткие требования к вычислительной мощности аппаратуры. Только совсем недавно, когда рядовому пользователю PC1)

стала доступна производительность супер-ЭВМ 70-х, нейросетевые методы решения прикладных задач стали приобретать популярность. Как мы увидим далее в этой лекции, даже сейчас "настоящие" параллельные нейрокомпьютеры еще слишком дороги и не получили пока широкого распространения. Что уж говорить о конце 50-х, начале 60-х, когда появились первые образцы нейрокомпьютеров.

Первый экспериментальный нейрокомпьютер Snark был построен Марвином Минским в 1951 году. Однако, он не был приспособлен к решению практически интересных задач, и первый успех нейрокомпьютинга связывают с разработкой другого американца - Френка Розенблатта - персептроном (от английского perception - восприятие) (Rosenblatt, 1961).
Персептрон был впервые смоделирован на универсальной ЭВМ IBM-704 в 1958 году, причем его обучение требовало около получаса машинного времени. Аппаратный вариант - Mark I Perceptron, был построен в 1960 году и предназначался для распознавания зрительных образов. Его рецепторное поле состояло из 400 пикселей (матрица фотоприемников 20x20), и он успешно справлялся с решением ряда задач - мог различать некоторые буквы. Однако по причинам, которые станут понятны по мере знакомства с теорией нейросетей, возможности первых персептронов были весьма ограничены. Позднее, в 1969 году Минский в соавторстве с Пейпертом дает математическое обоснование принципиальной, как им казалось, ограниченности персептронов (Minsky and Papert, 1969), что послужило началом охлаждения научных кругов к нейрокомпьютингу. Исследования в этом направлении были свернуты вплоть до 1983 года, когда они, наконец, получили финансирование от Агентства Перспективных Военных Исследований США, DARPA. Этот факт стал сигналом к началу нового нейросетевого бума.

Интерес широкой научной общественности к нейросетям пробудился в начале 80-х годов после теоретических работ физика Джона Хопфилда (Hopfield, 1982, 1984). Он и его многочисленные последователи обогатили теорию параллельных вычислений многими идеями из арсенала физики, такими как коллективные взаимодействия нейронов, энергия сети, температура обучения и т.д.

Однако, настоящий бум практических применений нейросетей начался после публикации Румельхартом с соавторами метода обучения многослойного персептрона, названного ими методом обратного распространения ошибки (error backpropagation) (Rumelhart et. al., 1986). Ограничения персептронов, о которых писали Минский и Пейперт, оказались преодолимыми, а возможности вычислительной техники - достаточными для решения широкого круга прикладных задач.

Далее в этой лекции мы вкратце опишем современное (правда чрезвычайно быстро меняющееся) состояние нейрокомпьютинга: нейросетевые продукты (как специализированное hardware, так и более доступное software), их сегодняшние применения, а также основные принципы нейровычислений.

Локальность и параллелизм вычислений

Массовый параллелизм нейро-вычислений, необходимый для эффективной обработки образов, обеспечивается локальностью обработки информации в нейросетях. Каждый нейрон реагирует лишь на локальную информацию, поступающую к нему в данный момент от связанных с ним таких же нейронов, без апелляции к общему плану вычислений, обычной для универсальных ЭВМ. Таким образом, нейросетевые алгоритмы локальны, и нейроны способны функционировать параллельно.

Нейро-эмуляторы

Доступность и возросшие вычислительные возможности современных компьютеров привели к широкому распространению программ, использующих принципы нейросетевой обработки данных, о которых мы поговорим подробнее в следующих разделах, но исполняемых на последовательных компьютерах. Этот подход не использует преимуществ присущего нейро-вычислениям параллелизма, ориентируясь исключительно на способность нейросетей решать неформализуемые задачи .

Нейросетевой консалтинг

Описание рынка нейро-продуктов будет не полным без упоминания о нейро-консалтинге. Вместо того, чтобы продавать готовые программы либо инструменты для их разработки, можно торговать и услугами. Например, до изобретения радио большим спросом пользовались барометры, как инструменты предсказания погоды. Теперь же мы просто узнаем погоду по радио или TV, а не предсказываем ее кустарными методами. Некоторые задачи, например такие, как предсказание рыночных временных рядов, являются настолько сложными, что доступны лишь настоящим профессионалам. Не каждая компания может позволить себе издержки, ассоциируемые с передовыми научными разработками (например, постоянное участие в международных конференциях). Поэтому приобретают популярность фирмы, единственной продукцией которых являются предсказания рынков. При большом числе клиентов цена таких предсказаний может быть весьма умеренной.

Примером здесь может служить Prediction Company, основанная в 1991 году физиками Дойном Фармером и Норманом Паккардом - специалистами в области динамического хаоса. Первый до этого руководил группой исследования сложных систем в ядерной лаборатории Лос Аламоса, а второй работал в Институте Перспективных Исследований в Принстоне (где когда-то трудился Эйнштейн). Продукция компании пользуется большим успехом среди Швейцарских банков, скупающих прогнозы "на корню" для игры на фондовых и валютных рынках.

Таблица 2.4. Секторы рынка нейросетевых программных продуктов

Сегмент рынка нейро-продуктовПреимущества продукцииНедостатки продукции

Нейро-пакеты общего назначения	Не требуют самостоятельного программирования, легко осваиваются, инструмент быстрого и дешевого решения прикладных задач	Не способны к расширению, не способны генерировать отчуждаемые приложения, не могут использоваться для разработки сложных систем или их подсистем
Системы разработки нейроприложений	Могут использоваться для создания сложных систем обработки данных в реальном времени (или их подсистем)	Требуют навыков программирования, более глубокого знания нейросетей
Готовые решения на основе нейросетей	Не предполагают знакомства пользователя с нейросетями, предоставляют комплексное решение проблемы	Как правило - дорогое удовольствие
Нейро-консалтинг	Не предполагает участия пользователя в получении прогнозов, потенциальная дешевизна услуг	Нет возможности дополнить предсказания своим know how. Доступность конфиденциальной информации

Преимущества нейро-эмуляторов

Преимущества таких "виртуальных" нейрокомпьютеров для относительно небольших задач очевидны:

Во-первых, не надо тратиться на новую аппаратуру, если можно загрузить уже имеющиеся компьютеры общего назначения. Во-вторых, пользователь не должен осваивать особенности программирования на спец-процессорах и способы их сопряжения с базовым компьютером. Наконец, универсальные ЭВМ не накладывают никаких ограничений на структуру сетей и способы их обучения, тогда как спец-процессоры зачастую имеют ограниченный набор "зашитых" в них функций активации и достигают пиковой производительности лишь на определенном круге задач.

В общем, если речь идет не о распознавании изображений в реальном времени или других приложениях такого рода, а, скажем, об обработке и анализе обычных баз данных, не имеет особого смысла связываться с нейро-ускорителями. Скорее всего, производительности хорошей PC окажется вполне достаточно. Поскольку большинство финансовых применений относится пока имено к этому классу задач, мы будем ориентировать нашего читателя на использование нейро-эмуляторов. Несколько условно нейро-software можно разделить на готовые нейро-пакеты общего назначения, более дорогие системы разработки нейроприложений, обладающие большими возможностями, но требующие и больших знаний, и, наконец, готовые комплексные решения с элементами нейросетевой обработки информации, обычно скрытыми от глаз пользователя.

Программирование: обучение, основанное на данных

Отсутствие глобального плана вычислений в нейросетях предполагает и особый характер их программирования. Оно также носит локальный характер: каждый нейрон изменяет свои "подгоночные параметры" - синаптические веса - в соответствии с поступающей к нему локальной информацией об эффективности работы всей сети как целого. Режим распространения такой информации по сети и соответствующей ей адаптации нейронов носит характер обучения. Такой способ программирования позволяет эффективно учесть специфику требуемого от сети способа обработки данных, ибо алгоритм не задается заранее, а порождается самими данными - примерами, на которых сеть обучается. Именно таким образом в процессе самообучения биологические нейросети выработали столь эффективные алгоритмы обработки сенсорной информации.

Характерной особенностью нейросетей является их способность к обобщению, позволяющая обучать сеть на ничтожной доле всех возможных ситуаций, с которыми ей, может быть, придется столкнуться в процессе функционирования. В этом их разительное отличие от обычных ЭВМ, программа которых должна заранее предусматривать их поведение во всех возможных ситуациях. Эта же их способность позволяет кардинально удешевить процесс разработки приложений.

Рынок нейропродукции

Объем рынка нейропродукции, структуру которого мы попытались выше очертить, растет стремительными темпами: по разным оценкам - от 30% до 50% в год, перевалив недавно за миллиард долларов (рисунок 2.2).

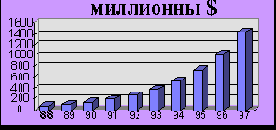
Рис. 2.2.  Рост объемов продаж нейропродукции

Такой же рост наблюдался в начале 80-х годов на формирующемся в то время рынке персональных компьютеров. Миллиардный оборот тогда явился сигналом для вступления на этот рынок гиганта компьютерной индустрии - IBM. Все мы прекрасно помним как в результате возникшей конкуренции за деньги конечного пользователя преобразился весь компьютерный мир…

Нейрокомпьютеры и их программные эмуляторы, естественно, интересны не сами по себе, а как инструмент решения практических задач. Только в этом случае нейропродукция будет обладать потребительской стоимостью и иметь соответствующий объем рынка. Где же и как используется нейросетевая продукция сегодня?

Сравнение стоимости обычных и нейро- вычислений

Производительность современных персональных компьютеров составляет примерно 107 операций с плавающей точкой в секунду (при тактовой частоте системной шины 66 МГц, положив в среднем 6 тактов на одну операцию). Итак, при стоимости всего на порядок больше обычных PC, нейроускоритель в несколько сот раз превосходит их в быстродействии. Таким образом, удельная стоимость современных нейровычислений примерно на порядок ниже, чем у традиционных компьютеров. Это всего лишь следствие специализации матричных процессоров (DSP), имеющих ту же элементную базу, что и универсальные микропроцессоры.

Однако, выигрыш на один порядок в стоимости вычислений редко когда способен стать решающим аргументом для использования специализированной аппаратуры, сопряженным с дополнительными затратами, в том числе на обучение персонала. Поэтому реально нейрокомпьютеры используются в специализированных системах, когда требуется обучать и постоянно переобучать сотни нейросетей, объединенных в единые информационные комплексы, или в системах реального времени, где скорость обработки данных критична.

Например, при обработке экспериментов на современных ускорителях элементарных частиц скорость поступления событий достигает десятков МГц, тогда как конечная информация записывается на ленту со скоростью десятки Гц. Т.е. требуется отбор одного события из миллиона - причем в реальном масштабе времени. Для этого используют несколько каскадов фильтрации событий. Здесь-то вычислительные возможности параллельных нейрокомпьютеров оказываются весьма кстати. Так, в эксперименте H1 на ускорителе HERA всю аппаратную часть фильтрации событий планируется реализовать на основе нейроплат CNAPS (данные 1994 г.).

Большинство же прикладных систем нейросетевой обработки данных использует эмуляцию нейросетей на обычных компьютерах, в частности на PC. Такие програмы называются нейро-эмуляторами.

Сравнение вычислительных возможностей искусственных и природных нейросетей

Из приведенных в предыдущих таблицах данных следует, что возможности современных нейрокомпьютеров пока довольно скромны, особенно в сравнении с биологическими нейросистемами (см. рисунок 2.1). Они едва-едва достигли уровня мухи и еще не дотягивают до таракана.

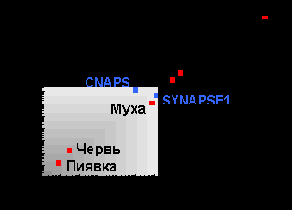
Рис. 2.1.  Сравнение современных нейрокомпьютеров с естественными нейросистемами

Вспомним, однако, искусство маневра, характерное для полета мухи, и возможности современных нейрокомпьютеров уже не покажутся такими уж скромными.

Типы обучения нейросети

Ошибка сети зависит, как уже говорилось, от конфигурации сети - совокупности всех ее синаптических весов. Но эта зависимость не прямая, а опосредованная. Ведь непосредственные значения весов скрыты от внешнего наблюдателя. Для него сеть - своего рода черный ящик, и оценивать ее работу он может лишь основываясь на ее поведении, т.е. на том, каковы значения выходов сети при данных входах. Иными словами, в общем виде функция ошибки имеет вид:

Здесь

- набор примеров (т.е. пар входов-выходов), на которых обучается нейросеть, а - реальные значения выходов нейросети, зависящие от конкретных значений ее синаптических весов. Такой способ обучения, когда действительный выход нейросети сравнивают с эталонным, называют обучением с учителем.

Иногда выходная информация известна не полностью. Например, вместо эталонных ответов известно лишь хуже или лучше данная конфигурация сети справляется с задачей (вспомним детскую игру "холоднее-горячее" или лабораторную мышь в лабиринте с лакомствами и электрошоком). Этот тип обучения называют обучением с подкреплением (reinforcement learning).

Вообще говоря, возможен и такой режим обучения, когда желаемые значения выходов вообще неизвестны, и сеть обучается только на наборе входных данных:

Такой режим обучения сети называют обучением без учителя. В этом случае сети предлагается самой найти скрытые закономерности в массиве данных. Так, избыточность данных допускает сжатие информации, и сеть можно научить находить наиболее компактное представление таких данных, т.е. произвести оптимальное кодирование данного вида входной информации.

Таблица 2.5. Сравнение режимов обучения нейросетей

Вид обучения:С "учителем"С "подкреплением"Без "учителя"

Что подается в качестве обучающих примеров	Набор пар входов-выходов	Оценка выходов сети	Только набор входных значений
Что требуется от сети	Найти функцию, обобщающую примеры, в случае дискретных - классифицировать входы. В целом - научиться реагировать схожим образом в схожих ситуациях.	Научиться заданной "правильной" линии поведения.	Найти закономерности в массиве данных, отыскать порождающую данные функцию распределения, найти более компактное описание данных.

С практической точки зрения, "помеченные" данные зачастую дороги и не столь многочисленны, как "непомеченные" , например, в случае, когда "учителем" является человек - эксперт. В силу этого обстоятельства на таких данных можно обучить лишь относительно простые и компактные нейросети. Напротив, нейросети, обучаемые без учителя часто используют для переработки больших массивов "сырых" данных - в качестве предобрабатывающих фильтров. Указанное различие, однако, исчезает, когда данные естественным образом распадаются на входы-выходы, например при предсказании временных рядов, где следующее значение ряда является выходом, а предыдущие несколько значений - соответствующими входами обучаемой нейросети.

Универсальность обучающих алгоритмов

Привлекательной чертой нейрокомпьютинга является единый принцип обучения нейросетей - минимизация эмпирической ошибки. Функция ошибки, оценивающая данную конфигурацию сети, задается извне - в зависимости от того, какую цель преследует обучение. Но далее сеть начинает постепенно модифицировать свою конфигурацию - состояние всех своих синаптических весов - таким образом, чтобы минимизировать эту ошибку. В итоге, в процессе обучения сеть все лучше справляется с возложенной на нее задачей.

Не вдаваясь в математические тонкости, образно этот процесс можно представить себе как поиск минимума функции ошибки

, зависящей от набора всех синаптических весов сети w (см. рисунок 2.5).

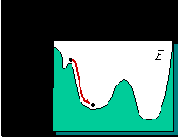
Рис. 2.5.  Обучение сети как задача оптимизации

Базовой идеей всех алгоритмов обучения является учет локального градиента в пространстве конфигураций для выбора траектории быстрейшего спуска по функции ошибки. Функция ошибки, однако, может иметь множество локальных минимумов, представляющих суб-оптимальные решения. Поэтому градиентные методы обычно дополняются элементами стохастической оптимизации, чтобы предотвратить застревание конфигурации сети в таких локальных минимумах. Идеальный метод обучения должен найти глобальный оптимум конфигурации сети .

В дальнейшем нам встретится множество конкретных методов обучения сетей с разными конфигурациями межнейронных связей. Чтобы не потерять за деревьями леса, полезно заранее ознакомиться с базовыми нейро-архитектурами. В следующем разделе мы приведем такого рода классификацию, основанную на способах кодирования информации в сетях (обучения) и декодирования (обработки) информации нейросетями.

Адаптивная оптимизации архитектуры сети

Итак, мы выяснили, что существует оптимальная сложность сети, зависящая от количества примеров, и даже получили оценку размеров скрытого слоя для двухслойных сетей. Однако в общем случае следует опираться не на грубые оценки, а на более надежные механизмы адаптации сложности нейросетевых моделей к данным для каждой конкретной задачи.

Для борьбы с переобучением в нейрокомпьютинге используются три основных подхода:

Ранняя остановка обучения Прореживание связей (метод от большого - к малому) Поэтапное наращивание сети (от малого - к большому)

Байесовский подход

Основная проблема статистики - обобщение эмпирических данных. В формализованном виде задача состоит в выборе наилучшей модели (гипотезы, объясняющей наблюдаемые данные) из некоторого доступного множества. Для решения этой задачи надо уметь оценивать степень достоверности той или иной гипотезы. Математическая формулировка этого подхода содержится в знаменитой теореме Байеса.

Обозначим весь набор имеющихся данных

, а гипотезы, объясняющие эти данные (в нашем случае - нейросети), как . Предполагается, что каждая такая гипотеза объясняет данные с большей или меньшей степенью вероятности . Теорема Байеса дает решение обратной задачи - определить степень достоверности гипотез , исходя из их успехов в объяснении данных. Согласно этой теореме, достоверность гипотезы пропорциональна ее успеху, а также ее априорной вероятности, , известной из других соображений, не относящихся к данной серии наблюдений:

В этом современном виде теорема Байеса была на самом деле сформулирована Лапласом. Томасу Байесу принадлежит сама постановка задачи. Он сформулировал ее как обратную известной задаче Бернулли. Если Бернулли искал вероятность различных исходов бросания "кривой" монеты, то Байес, наоборот, стремился определить степень этой "кривизны" по эмпирически наблюдаемым исходам бросания монеты. В его решении отсутствовала априорная вероятность.

Наилучшая модель определяется максимизацией

или ее логарифма, что дает один и тот же результат в силу монотонности логарифмической функции. Логарифмы удобны тем, что произведение вероятностей независимых событий они переводят в сумму их логарифмов:

(1)

(Знаменатель не зависит от модели и не влияет на выбор лучшей.)

Выписанная выше формула является базовой для понимания основ обучения нейросетей, т.к. она задает критерий оптимальности обучения, к которому надо стремиться. Мы еще неоднократно вернемся к ней на протяжении этой лекции. Обсудим, прежде всего значение обоих членов в правой части полученного выражения.

Двухслойные персептроны

Возможности линейного дискриминатора весьма ограничены. Он способен правильно решать лишь ограниченный круг задач - когда классы, подлежащие классификации линейно-разделимы, т.е. могут быть разделены гиперплоскостью ( рисунок 3.2).

Рис. 3.2.  Пример линейно разделимых (слева) и линейно-неразделимых (справа) множеств

В d-мерном пространстве гиперплоскость может разделить произвольным образом лишь d+1 точки. Например, на плоскости можно произвольным образом разделить по двум классам три точки, но четыре - в общем случае уже невозможно (см. рисунок 3.2). В случае плоскости это очевидно из приведенного примера, для большего числа измерений - следует из простых комбинаторных соображений. Если точек больше чем d+1 всегда существуют такие способы их разбиения по двум классам, которые нельзя осуществить с помощью одной гиперплоскости. Однако, этого можно достичь с помощью нескольких гиперплоскостей.

Для решения таких более сложных классификационных задач необходимо усложнить сеть, вводя дополнительные (их называют скрытыми) слои нейронов, производящих промежуточную предобработку входных данных таким образом, чтобы выходной нейрон-классификатор получал на свои входы уже линейно-разделимые множества.

Причем легко показать, что, в принципе, всегда можно обойтись всего лишь одним скрытым слоем, содержащим достаточно большое число нейронов. Действительно, увеличение скрытого слоя повышает размерность пространства, в котором выходной нейрон производит дихотомию, что, как отмечалось выше, облегчает его задачу.

Не вдаваясь в излишние подробности резюмируем результаты многих исследований аппроксимирующих способностей персептронов.

Сеть с одним скрытым слоем, содержащим H нейронов со ступенчатой функцией активации, способна осуществить произвольную классификацию Hd точек d-мерного пространства (т.е. классифицировать Hd примеров). Одного скрытого слоя нейронов с сигмоидной функцией активации достаточно для аппроксимации любой границы между классами со сколь угодно высокой точностью.

Для задач аппроксимации последний результат переформулируется следующим образом:

Одного скрытого слоя нейронов с сигмоидной функцией активации достаточно для аппроксимации любой функции со сколь угодно высокой точностью. (Более того, такая сеть может одновременно аппроксимировать и саму функцию и ее производные.)

Точность аппроксимации возрастает с числом нейронов скрытого слоя. При H нейронах ошибка оценивается как

. Эта оценка понадобится нам в дальнейшем.

Градиентное обучение

Наиболее общим способом оптимизации нейросети является итерационная (постепенная) процедура подбора весов, называемая обучением, в данном случае - обучением с учителем, поскольку опирается на обучающую выборку примеров

, например - примеров правильной классификации.

Когда функционал ошибки задан, и задача сводится к его минимизации, можно предложить, например, следующую итерационную процедуру подбора весов:

или, что то же самое:

Здесь

- темп обучения на шаге . Можно показать, что постепенно уменьшая темп обучения, например по закону , описанная выше процедура приводит к нахождению локального минимума ошибки.

Исторически наибольшую трудность на пути к эффективному правилу обучения многослойных персептронов вызвала процедура эффективного расчета градиента функции ошибки

. Дело в том, что ошибка сети определяется по ее выходам, т.е. непосредственно связаная лишь с выходным слоем весов. Вопрос состоял в том, как определить ошибку для нейронов на скрытых слоях, чтобы найти производные по соответствующим весам. Нужна была процедура передачи ошибки с выходного слоя к предшествующим слоям сети, в направлении обратном обработке входной информации. Поэтому такой метод, когда он был найден, получил название метода обратного распространения ошибки.

Использование алгоритма back-propagation

При оценке значения алгоритма back-propagation важно различать нахождение градиента ошибки

и его использование для обучения. Иногда под этим именем понимают именно конкретный тип итерационного обучения, предложенный в статье Румельхарта с соавторами. Этот простейший тип обучения (метод скорейшего спуска) обладает рядом недостатков. Существуют много гораздо более хороших алгоритмов обучения, использующих градиент ошибки более эффективно. Ниже мы перечислим некоторые из них, наиболее часто используемые на практике. Подчеркнем, однако, что все они так или иначе используют изложенный выше метод back-propagation для нахождения градиента ошибки.

Итак, простейший способ использования градиента при обучении - изменение весов пропорционально градиенту - т.н метод наискорейшего спуска:

Этот метод оказывается, однако, чрезвычайно неэффективен в случае, когда производные по различным весам сильно отличаются, т.е. рельеф функции ошибки напоминает не яму, а длинный овраг. (Это соответствует ситуации, когда активация некоторых из сигмоидных нейронов близка по модулю к 1 или, что то же самое - когда модуль некоторых весов много больше 1). В этом случае для плавного уменьшения ошибки необходимо выбирать очень маленький темп обучения, диктуемый максимальной производной (шириной оврага), тогда как расстояние до минимума по порядку величины определяется минимальной производной (длиной оврага). В итоге обучение становится неприемлемо медленным. Кроме того, на самом дне оврага неизбежно возникают осцилляции, и обучение теряет привлекательное свойство монотонности убывания ошибки.

Рис. 3.5.  Неэффективность метода скорейшего спуска: градиент направлен не в сторону минимума

Простейшим усовершенствованием метода скорейшего спуска является введение момента , когда влияние градиента на изменение весов накапливается со временем:

Качественно влияние момента на процесс обучения можно пояснить следующим образом. Допустим, что градиент меняется плавно, так что на протяжении некоторого времени его изменением можно пренебречь (мы находимся далеко от дна оврага).
Тогда изменение весов можно записать в виде:

т.е. в этом случае эффективный темп обучения увеличивается, причем существенно, если момент . Напротив, вблизи дна оврага, когда направление градиента то и дело меняет знак из-за описанных выше осцилляций, эффективный темп обучения замедляется до значения близкого к :


Рис. 3.6.  Введение инерции в алгоритм обучения позволяет адаптивно менять скорость обучения


Дополнительное преимущество от введения момента - появляющаяся у алгоритма способность преодолевать мелкие локальные минимумы. Это свойство можно увидеть, записав разностное уравнение для обучения в виде дифференциального. Тогда обучение методом скорейшего спуска будет описываться уравненем движения тела в вязкой среде: . Введение момента соответствует появлению у такого гипотетического тела инерции, т.е. массы: . В итоге, "разогнавшись", тело может по инерции преодолевать небольшие локальные минимумы ошибки, застревая лишь в относительно глубоких, значимых минимумах.

Одним из недостатков описанного метода является введение еще одного глобального настроечного параметра. Мы же, наоборот, должны стремиться к отсутствию таких навязываемых алгоритму извне параметров. Идеальной является ситуация, когда все параметры обучения сами настраиваются в процессе обучения, извлекая информацию о характере рельефа функции ошибки из самого хода обучения. Примером весьма удачного алгоритма обучения является т.н. RPROP (от resilient - эластичный), в котором каждый вес имеет свой адаптивно настраиваемый темп обучения.

RPROP стремится избежать замедления темпа обучения на плоских "равнинах" ландшафта функции ошибки, характерного для схем, где изменения весов пропорциональны величине градиента. Вместо этого RPROP использует лишь знаки частных производных по каждому весу.

Величина шага обновления - своя для каждого веса и адаптируется в процессе обучения:

Если знак производной по данному весу изменил направление, значит предыдущее значение шага по данной координате было слишком велико, и алгоритм уменьшает его в раз.В противном случае шаг увеличивается в раз для ускорения обучения вдали от минимума.

Мы не затронули здесь более изощренных методов обучения, таких как метод сопряженного градиента, а также методов второго порядка, которые используют не только информацию о градиенте функции ошибки, но и информацию о вторых производных. Их разбор вряд ли уместен при первом кратком знакомстве с основами нейрокомпьютинга.

Эффективность алгоритма back-propagation

Важность изложенного выше алгоритма back-propagation в том, что он дает чрезвычайно эффективный способ нахождения градиента функции ошибки

. Если обозначить общее число весов в сети как W, то необходимое для вычисления градиента число операций растет пропорционально W , т.е. этот алгоритм имеет сложность O(W). Напротив, прямое вычисление градиента по формуле потребовала бы W прямых прогонов через сеть, требующих O(W) операций каждый. Таким образом "наивный" алгоритм имеет сложность , что существенно хуже, чем у алгоритма back-propagation.

Конструктивные алгоритмы

Эти алгоритмы характеризуются относительно быстрым темпом обучения, поскольку разделяют сложную задачу обучения большой многослойной сети на ряд более простых задач, обычно - обучения однослойных подсетей, составляющих большую сеть. Поскольку сложность обучения пропорциональна квадрату числа весов, обучение "по частям" выгоднее, чем обучение целого:

Для примера опишем так называемую каскад-корреляционную методику обучения нейросетей. Конструирование сети начинается с единственного выходного нейрона и происходит путем добавления каждый раз по одному промежуточному нейрону (см. рисунок 3.10).

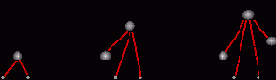
Рис. 3.10.  Каскад-корреляционные сети: добавление промежуточных нейронов с фиксированными весами (тонкие линии)

Эти промежуточные нейроны имеют фиксированные веса, выбираемые таким образом, чтобы выход добавляемых нейронов в максимальной степени коррелировал с ошибками сети на данный момент (откуда и название таких сетей). Поскольку веса промежуточных нейронов после добавления не меняются, их выходы для каждого значения входов можно вычислить лишь однажды. Таким образом, каждый добавляемый нейрон можно трактовать как дополнительный признак входной информации, максимально полезный для уменьшения ошибки обучения на данном этапе роста сети. Оптимальная сложность сети может определяться, например, с помощью валидационного множества.

Метод обратного распространения ошибки

Ключ к обучению многослойных персептронов оказался настолько простым и очевидным, что, как оказалось, неоднократно переоткрывался.

Так, например, базовый алгоритм был изложен в диссертации Пола Вербоса (Paul Werbos) 1974 года, но тогда не привлек к себе должного внимания. Рождение алгоритма back-propagation (обратного распространения ошибки) для широкой публики связано с работой группы PDP (Parallel Distributed Processing), освещенной в двухтомном труде 1986г. Именно там в статье Румельхарта, Хинтона и Уильямса была изложена теория обучения многослойного персептрона.

Между тем, в случае дифференцируемых функций активации рецепт нахождения производных по любому весу сети дается т.н. цепным правилом дифференцирования, известным любому первокурснику. Суть метода back-propagation - в эффективном воплощении этого правила.

Фрэнк Розенблаттом использовал в своем персептроне недифференцируемую ступенчатую функцию активации. Возможно, именно это помешало ему найти эфективный алгоритм обучения, хотя сам термин Back Propagation восходит к его попыткам обобщить свое правило обучения одного нейрона на многослойную сеть. Как знать, используй Розенблатт вместо ступенчатой функции активации - сигмоидную, может быть его судьба сложилась бы по-другому.1)

Разберем этот ключевой для нейрокомпьютинга метод несколько подробнее. Обозначим входы n-го слоя нейронов

. Нейроны этого слоя вычисляют соответствующие линейные комбинации: и передают их на следующий слой, пропуская через нелинейную функцию активации (для простоты - одну и ту же, хотя это совсем необязательно):

Для построения алгоритма обучения нам надо знать производную ошибки по каждому из весов сети:

Таким образом, вклад в общую ошибку каждого веса вычисляется локально, простым умножением невязки нейрона

на значение соответствующего входа. (Из-за этого, в случае когда веса изменяют по направлению скорейшего спуска , такое правило обучения называют дельта-правилом.)

Входы каждого слоя вычисляются последовательно от первого слоя к последнему во время прямого распространения сигнала:

, а невязки каждого слоя вычисляются во время обратного распространения ошибки от последнего слоя (где они определяются по выходам сети) к первому:

Последняя формула получена применением цепного правила к производной

и означает, что чем сильнее учитывается активация данного нейрона на следующем слое, тем больше его ответственность за общую ошибку.

Нейрон - классификатор

Простейшим устройством распознавания образов, принадлежащим к рассматриваемому классу сетей, является одиночный нейрон, превращающий входной вектор признаков в скалярный ответ, зависящий от линейной комбинации входных переменных:

Здесь и далее мы предполагаем наличие у каждого нейрона дополнительного единичного входа с нулевым индексом, значение которого постоянно:

. Это позволит упростить выражения, трактуя все синаптические веса w j, включая порог w0, единым образом.

Скалярный выход нейрона можно использовать в качестве т.н. дискриминантной функции. Этим термином в теории распознавания образов называют индикатор принадлежности входного вектора к одному из заданных классов. Так, если входные векторы могут принадлежать одному из двух классов, нейрон способен различить тип входа, например, следующим образом:

если , входной вектор принадлежит первому классу, в противном случае - второму.

Поскольку дискриминантная функция зависит лишь от линейной комбинации входов, нейрон является линейным дискриминатором. В некоторых простейших ситуациях линейный дискриминатор - наилучший из возможных, а именно - в случае когда вероятности принадлежности входных векторов к классу k задаются гауссовыми распределениями

с одинаковыми ковариационными матрицами . В этом случае границы, разделяющие области, где вероятность одного класса больше, чем вероятность остальных, состоят из гиперплоскостей (см. рисунок 3.1 иллюстрирующий случай двух классов).

Рис. 3.1.  Линейный дискриминатор дает точное решение в случае если вероятности принадлежности к различным классам - гауссовы, с одинаковым разбросом и разными центрами в пространстве параметров

В более общем случае поверхности раздела между классами можно описывать приближенно набором гиперплоскостей - но для этого уже потребуется несколько линейных дискриминаторов - нейронов.

Оптимизация размера сети

Итак, мы оценили обе составляющих ошибки обобщения сети. Важно, что эти составляющие по-разному зависят от размера сети (числа весов), что предполагает возможность выбора оптимального размера, минимизирующего общую ошибку:

Минимум ошибки (знак равенства) достигается при оптимальном числе весов в сети

соответствующих числу нейронов в скрытом слое равному по порядку величины:

Этот результат можно теперь использовать для получения окончательной оценки сложности обучения (C - от английского complexity)

Отсюда можно сделать следующий практический вывод: нейроэмуляторам с производительностью современных персональных компьютеров (

операций в секунду) вполне доступны анализ баз данных с числом примеров

и размерностью входов

. Типичное время обучения при этом составит секунд, т.е. от десятков минут до несколько часов. Поскольку производственный цикл нейроанализа предполагает обучение нескольких, иногда - многих сетей, такой размер баз данных, представляется предельным для нейротехнологии на персональных компьютерах. Эти оценки поясняют также относительно позднее появление нейрокомпьютинга: для решения практически интересных задач требуется производительность суперкомпьютеров 70-х годов.

Согласно полученным выше оценкам ошибка классификации на таком классе задач порядка 10%. Это, конечно, не означает, что с такой точностью можно предсказывать что угодно. Многие относительно простые задачи классификации решаются с большей точностью, поскольку их эффективная размерность гораздо меньше, чем число входных переменных. Напротив, для рыночных котировок достижение соотношения правильных и неправильных предсказаний 65:35 уже можно считать удачей. Действительно, приведенные выше оценки предполагали отсутствие случайного шума в примерах. Шумовая составляющая ошибки предсказаний должна быть добавлена к полученной выше оценке. Для сильно зашумленных рыночных временных рядов именно она определяет предельную точность предсказаний. Подробнее эти вопросы будут освещены в отдельной лекции, посвященной предсказанию зашумленных временных рядов.

Другой вывод из вышеприведенных качественных оценок - обязательность этапа предобработки высокоразмерных данных. Невозможно классифицировать непосредственно картинки с размерностью . Из оценки точности классификации следует, что это потребует числа обучающих примеров по крайней мере такого же порядка, т.е. сложность обучения будет порядка . Современным нейрокомпьютерам с производительностью операций в секунду потребовалось бы несколько лет обучения распознаванию таких образов. Зрительная система человека, составляющая несколько процентов коры головного мозга, т.е. обладающая производительностью способна обучаться распознаванию таких образов за несколько часов2). В действительности, зрительный нерв содержит как раз около нервных волокон. Напомним, однако, что в сетчатке глаза содержится порядка клеток-рецепторов. Таким образом, уже в самом глазе происходит существенный этап предобработки исходного сигнала, и в мозг поступает уже такая информация, которую он способен усвоить. (Непосредственное распознавание образов с потребовало бы обучения на протяжении секунд, т.е. около 300 лет.)

Методы предобработки сигналов и формирования относительно малоразмерного пространства признаков являются важнейшей составляющей нейроанализа и будут подробно рассмотрены далее в отдельной лекции.

Оптимизация размеров сети

В описанных до сих пор методах обучения значения весов подбиралось в сети с заданной топологией связей. А как выбирать саму структуру сети: число слоев и количество нейронов в этих слоях? Решающим, как мы увидим, является выбор соотношения между числом весов и числом примеров. Зададимся поэтому теперь следующим вопросом:

Как связаны между собой число примеров P и число весов в сети W?

Ошибка аппроксимации

Рассмотрим для определенности двухслойную сеть (т.е. сеть с одним скрытым слоем). Точность аппроксимации функций такой сетью, как уже говорилось, возрастает с числом нейронов скрытого слоя. При

нейронах ошибка оценивается как . Поскольку число выходов сети не превышает, а как правило - много меньше числа входов, основное число весов в двухслойной сети сосредоточено в первом слое, т.е. .В этом случае средняя ошибка аппроксимации выразится через общее число весов в сети следующим образом: где d- размерность входов.

Наши недостатки, как известно - продолжения наших достоинств. И упомянутая выше универсальность персептронов превращается одновременно в одну из главных проблем обучающихся алгоритмов, известную как проблема переобучения.

Ошибка, связанная со сложностью модели

Описание сети сводится, в основном, к передаче значений ее весов. При заданной точности такое описание потребует порядка

бит. Следовательно удельную ошибку на один пример, связанную со сложностью модели, можно оценить следующим образом:

Она, как мы видим, монотонно спадает с ростом числа примеров.

Действительно, для однозначного определения подгоночных параметров (весов сети) по

заданным примерам необходимо, чтобы система уравнений была переопределена, т.е. число параметров было больше числа уравнений. Чем больше степень переопределенности, тем меньше результат обучения зависит от конкретного выбора подмножества обучающих примеров. Определенная выше составляющая ошибки обобщения, как раз и связана с вариациями решения, обусловленными конечностью числа примеров.1)

Основы индуктивного метода

Прежде чем ответить на этот вопрос, следует задать критерий оптимальности. Поскольку нейросети осуществляют статистическую обработку данных, нам следует обратиться к основам математической статистики - индуктивному методу.

Переобучение

Суть этой проблемы лучше всего объяснить на конкретном примере. Пусть обучающие примеры порождаются некоторой функцией, которую нам и хотелось бы воспроизвести. В теории обучения такую функцию называют учителем. При конечном числе обучающих примеров всегда возможно построить нейросеть с нулевой ошибкой обучения, т.е. ошибкой, определенной на множестве обучающих примеров. Для этого нужно взять сеть с числом весов большим, чем число примеров. Действительно, чтобы воспроизвести каждый пример у нас имеется P уравнений для W неизвестных. И если число неизвестных меньше числа уравнений, такая система является недоопределенной и допускает бесконечно много решений. В этом-то и состоит основная проблема: у нас не хватает информации, чтобы выбрать единственное правильное решение - функцию-учителя. В итоге выбранная случайным образом функция дает плохие предсказания на новых примерах, отсутствовавших в обучающей выборке, хотя последнюю сеть воспроизвела без ошибок. Вместо того, чтобы обобщить известные примеры, сеть запомнила их. Этот эффект и называется переобучением.

На самом деле, задачей теории обучения является не минимизация ошибки обучения, а минимизация ошибки обобщения, определенной для всех возможных в будущем примеров. Именно такая сеть будет обладать максимальной предсказательной способностью. И трудность здесь состоит в том, что реально наблюдаемой является именно и только ошибка обучения. Ошибку обобщения можно лишь оценить, опираясь на те или иные соображения.

В этой связи вспомним изложенный в начале этой лекции принцип минимальной длины описания. Согласно этому общему принципу, ошибка предсказаний сети на новых данных определяется общей длиной описания данных с помощью модели вместе с описанием самой модели:

Первый член этого выражения отвечает наблюдаемой ошибке обучения. Мы оценили его выше. Теперь обратимся к оценке второго члена, регуляризирующего обучение.

Персептрон Розенблатта

Исторически, первые персептроны, предложенные Фрэнком Розенблаттом в 1958 г., имели два слоя нейронов. Однако, собственно обучающимся был лишь один, последний слой. Первый (скрытый) слой состоял из нейронов с фиксированными случайными весами. Эти, по терминологии Розенблатта - ассоциирующие, нейроны получали сигналы от случайно выбранных точек рецепторного поля. Именно в этом признаковом пространстве персептрон осуществлял линейную дискриминацию подаваемых на вход образов (см. рисунок 3.3).

Рис. 3.3.  Персептрон Розенблатта имел один слой обучаемых весов, на входы которого подавались сигналы с d = 512 ассоциирующих нейронов со случайными фиксированными весами, образующие признаковое пространство для 400-пиксельных образов

Результаты своих исследований Розенблатт изложил в книге "Принципы нейродинамики: Персептроны и теория механизмов мозга". Уже из самого названия чувствуется какое большое значение придавалось этому относительно простому обучающемуся устройству. Однако, многочисленные эксперименты показали неровный характер обучаемости персептронов. Некоторые задачи решались относительно легко, тогда как другие - вообще не поддавались обучению. В отсутствие теории объяснить эти эксперименты и определить перспективы практического использования персептронов было невозможно.

Подобного рода теория появилась к 1969г. с выходом в свет книги Марвина Минского и Сеймура Пейперта "Персептроны". Минский и Пейперт показали, что если элементы скрытого слоя фиксированы, их количество либо их сложность экспоненциально возрастает с ростом размерности задачи (числа рецепторов). Тем самым, теряется их основное преимущество - способность решать задачи произвольной сложности при помощи простых элементов.

Реальный же выход состоял в том, чтобы использовать адаптивные элементы на скрытом слое, т.е. подбирать веса и первого и второго слоев. Однако в то время этого делать не умели. Каким же образом находить синаптические веса сети, дающие оптимальную классификацию входных векторов?

Персептроны. Прототипы задач

Сети, о которых пойдет речь в этой лекции, являются основной "рабочей лошадкой" современного нейрокомпьютинга. Подавляющее большинство приложений связано именно с применением таких многослойных персептронов или для краткости просто персептронов (напомним, что это название происходит от английского perception - восприятие, т.к. первый образец такого рода машин предназначался как раз для моделирования зрения). Как правило, используются именно сети, состоящие из последовательных слоев нейронов. Хотя любую сеть без обратных связей можно представить в виде последовательных слоев, именно наличие многих нейронов в каждом слое позволяет существенно ускорить вычисления используя матричные ускорители.

В немалой степени популярность персептронов обусловлена широким кругом доступных им задач. В общем виде они решают задачу аппроксимации многомерных функций, т.е. построения многомерного отображения

, обобщающего заданный набор примеров .

В зависимости от типа выходных переменных (тип входных не имеет решающего значения), аппроксимация функций может принимать вид

Классификации (дискретный набор выходных значений), или Регрессии (непрерывные выходные значения)

Многие практические задачи распознавания образов, фильтрации шумов, предсказания временных рядов и др. сводится к этим базовым прототипическим постановкам.

Причина популярности персептронов кроется в том, что для своего круга задач они являются во-первых универсальными, а во-вторых - эффективными с точки зрения вычислительной сложности устройствами. В этой лекции мы затронем оба аспекта.

Принцип максимального правдоподобия (maximum likelihood)

Заметим, прежде всего, что второй член в правой части выражения не зависит от данных. Первый же, отражающий эмпирический опыт, как правило, имеет вид колокола тем более узкого, чем больше объем имеющихся в распоряжении данных (см. рисунок 3.4).

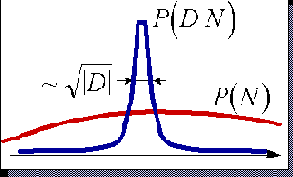
Рис. 3.4.  Качественная зависимость априорной и эмпирической составляющих формулы Байеса. Чем больше данных - тем точнее можно выбрать проверяемую гипотезу

Действительно, чем больше данных - тем точнее может быть проверены следствия конкурирующих гипотез, и, следовательно, тем точнее будет выбор наилучшей.

Следовательно, при стремлении количества данных к бесконечности, последним членом можно пренебречь. Это приближение:

получило название принципа максимального правдоподобия (Фишер) и характерно для т.н. параметрической статистики, в которой модель представляет собой семейство решений с небольшим и фиксированным набором параметров.

Отрицательный логарифм вероятности имеет смысл эмпирической ошибки при подгонке данных с помощью имеющихся в моделе свободных параметорв.

Например, в задаче аппроксимации функций обычно предполагается, что данные порождаются некоторой неизвестной функцией, которую и надо восстановить, но их "истинные" значения искажены случайным гауссовым шумом. Таким образом, условная вероятность набора данных

для модели , зависящей от настраиваемых параметров w, имеет гауссово распределение:

Отрицательный логарифм, таким образом, пропорционален сумме квадратов, и аппроксимация функции сводится к минимизации среднеквадратичной ошибки:

Принцип минимальной длины описания (minimum description length)

В случае нейросетевого моделирования число параметров как правило велико, более того, размер сети как правило соотносится с объемом обучающей выборки, т.е. число параметров зависит от числа данных. В принципе, как отмечалось далее, взяв достаточно большую нейросеть, можно приблизить имеющиеся данные со сколь угодно большой точностью. Между тем, зачастую это не то, что нам надо. Например, правильная аппроксимация зашумленной функции по определению должна давать ошибку - порядка дисперсии шума.

Учет второго члена формулы (1) позволяет наложить необходимые ограничения на сложность модели, подавляя, например, излишнее количество настроечных параметров. Смысл совместной оптимизации эмпирической ошибки и сложности модели дает принцип минимальной длины описания.

Согласно этому принципу следует минимизировать общую длину описания данных с помощью модели и описания самой модели. Чтобы увидеть это перепишем формулу (1) в виде:

Первый член, как мы убедились, есть эмпирическая ошибка. Чем она меньше - тем меньше бит потребуется для исправления предсказаний модели. Если модель предсказывает все данные точно, длина описания ошибки равна нулю. Второй член имеет смысл количества информации, необходимого для выбора конкретной модели из множества с априорным распределением вероятностей P(N).

Очень сильный результат теории индуктивного вывода, принадлежащий Рисанену, ограничивает ожидаемую ошибку модели на новых данных степенью сжатия информации с помощью этой модели. Чем меньше описанная выше суммарная длина описания, тем надежнее предсказания такой модели.

Этот вывод пригодится нам позднее - для выбора оптимального размера нейросетей. Пока же предположим, что цель обучения сформулирована - имеется подлежащий минимизации функционал ошибки

, зависящий от всех настроечных весов нейросети. Наша ближайшая задача - понять каким образом можно найти значения этих весов, минимизируещие такой функционал.

Прореживание связей

Эта методика стремится сократить разнообразие возможных конфигураций обученных нейросетей при минимальной потере их аппроксимирующих способностей. Для этого вместо колоколообразной формы априорной функции распределения весов, характерной для обычного обучения, когда веса "расползаются" из начала координат, применяется такой алгоритм обучения, при котором функция распределения весов сосредоточена в основном в "нелинейной" области относительно обльших значений весов (см.

рисунок 3.9).

Рис. 3.9.  Подавление малых значений весов в методе прореживания связей

Этого достигают введением соответствующей штрафной составляющей в функционал ошибки. Например, априорной функции распределения:

имеющую максимум в вершинах гиперкуба с

, соответствует штрафной член:

в функционале ошибки. Дополнительная составляющая градиента

исчезающе мала для больших весов,

, и пропорциональна величине малых весов, . Соответственно, на больших штрафная функция практически не сказывается, тогда как малые веса экспоненциально затухают.

Таким образом, происходит эффективное вымывание малых весов (weights elimination), т.е. прореживание малозначимых связей. Противоположная методика предполагает, напротив, поэтапное наращивание сложности сети. Соответствующее семейство алгоритмов обучения называют конструктивными алгоритмами.

Ранняя остановка обучения

Обучение сетей обычно начинается с малых случайных значений весов. Пока значения весов малы по сравнением с характерным масштабом нелинейной функции активации (обычно принимаемом равным единице), вся сеть представляет из себя суперпозицию линейных преобразований, т.е. является также линейным преобразованием с эффективным числом параметров равным числу входов, умноженному на число выходов. По мере возрастания весов и степень нелинейности, а вместе с ней и эффективное число параметров возрастает, пока не сравняется с общим числом весов в сети.

В методе ранней остановки обучение прекращается в момент, когда сложность сети достигнет оптимального значения. Этот момент оценивается по поведению во времени ошибки валидации. Рисунок 3.8. дает качественное представление об этой методике.

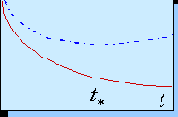
Рис. 3.8.  Ранняя остановка сети в момент минимума ошибки валидации (штрих-пунктирная кривая). При этом обычно ошибка обучения (сплошная кривая) продолжает понижаться

Эта методика привлекательна своей простотой. Но она имеет и свои слабые стороны: слишком большая сеть будет останавливать свое обучение на ранних стадиях, когда нелинейности еще не успели проявиться в полную силу. Т.е. эта методика чревата нахождением слабо-нелинейных решений. На поиск сильно нелинейных решений нацелен метод прореживания весов, который, в отличае от предыдущего, эффективно подавляет именно малые значения весов.

Валидация обучения

Прежде всего, для любого из перечисленных методов необходимо определить критерий оптимальной сложности сети - эмпирический метод оценки ошибки обобщения. Поскольку ошибка обобщения определена для данных, которые не входят в обучающее множество, очевидным решением проблемы служит разделение всех имеющихся в нашем распоряжении данных на два множества: обучающее - на котором подбираются конкретные значения весов, и валидационного - на котором оценивается предсказательные способности сети и выбирается оптимальная сложность модели. На самом деле, должно быть еще и третье - тестовое множество, которое вообще не влияет на обучение и используется лишь для оценки предсказательных возможностей уже обученной сети.

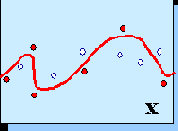
Рис. 3.7.  Обучающее (темные точки) и валидационные (светлые точки) множества примеров

Возможности многослойных персептронов

Изучение возможностей многослойных персептронов удобнее начать со свойств его основного компонента и одновременно простейшего персептрона - отдельного нейрона.

Выбор функции активации

Монотонные функции активации

не влияют на классификацию. Но их значимость можно повысить, выбрав таким образом, чтобы можно было трактовать выходы нейронов как вероятности принадлежности к соответствующему классу, что дает дополнительную информацию при классификации. Так, можно показать, что в упомянутом выше случае гауссовых распределений вероятности, сигмоидная функция активации нейрона дает вероятность принадлежности к соответствующему классу.

Вычислительная сложность обучения

Ранее при обсуждении истории нейрокомпьютинга мы ссылались на относительную трудоемкость процесса обучения. Чтобы иметь хотя бы приблизительное представление о связанных с обучением вычислительных затратах, приведем качественную оценку вычислительной сложности алгоритмов обучения.

Пусть как всегда W - число синаптических весов сети (weights), а P - число обучающих примеров (patterns). Тогда для однократного вычисления градиента функции ошибки

требуется порядка PW операций. Допустим для простоты, что мы достаточно близки к искомому минимуму и можем вблизи этого минимума аппроксимировать функцию ошибки квадратичным выражением . Здесь - матрица вторых производных в точке минимума . Оценив эту матрицу по локальной информации (для чего потребуется операций метода back-propagation), можно попасть из любой точки в минимум за один шаг. На этой стратегии построены методы вторго порядка (метод Ньютона). Альтернативная стратегия - найти требуемые параметров за шагов метода первого порядка, затратив на каждом шаге операций. Именно такую скорость сходимости ( итераций) имеют лучшие алгоритмы первого порядка (например, метод сопряженного градиента). В обоих случаях оптимистическая оценка сложности обучения сети (т.к. она получена для простейшего из всех возможных - квадратичного - рельефа) составляет операций.

---

---