Определение значимости параметров на основании функции оценки

Есть набор

, размерности -мерный вектор параметров и функция оценки , оценивающая работу системы с параметрами на векторе (например, расстояние от вектора выходных сигналов системы до нужного ответа или до множества правильно интерпретируемых ответов). Требуется выделить наименее значимые параметры и компоненты данных и модифицировать систему, отбрасывая наименее значимые параметры. Процедура отбрасывания неоднозначна. Простейший вариант - обращение в ноль - не всегда лучший: он не учитывает корреляции между данными. Учитывая корреляцию, следует отбрасываемые компоненты заменять на функции остающихся компонент.

Пусть для каждого

определено фиксированное значение . Отбрасывание -ой компоненты для -го примера означает приравнивание . В качестве простейшего варианта примем и для любого полагаем

(параметры обращаются в ноль, данные заменяются средним по выборке). Более тонкие методы предполагают замену отбрасываемых параметров и сигналов на некоторые функции оставшихся.

Определение значимости параметров по изменению выходных сигналов системы

Значимость параметров определяется практически так же, как и с помощью функции оценки. Пусть

- вектор данных, а - вектор параметров. Пусто задан набор векторов , на которых будет оцениваться функционирование системы, и определены значения (в простейшем случае ).

Вычислим в линейном приближении изменение вектора

при обращении

в

и в :

Пусть в пространстве выходных сигналов системы задана некоторая норма (например, евклидова). Тогда положим:

Таким образом, для каждого

и любого

определен вектор показателей значимости. Координаты вектора соответствуют точкам

. Теперь нужно вычислить норму этого вектора и объявить ее показателем значимости (можно в качестве нормы взять максимум модуля или сумму модулей). При использовании евклидовой нормы в пространстве выходных сигналов бывает удобно и далее выбирать такую же норму, полагая:

Подход к определению значимости через изменение выходного сигнала не имеет альтернатив в том случае, когда рассматриваемая система является лишь подсистемой в некоторой системе (например, сумматор или нейрон в нейронной сети). Тогда при изменении параметров этой подсистемы приходится ограничиться требованием: выходной сигнал подсистемы должен изменяться как можно меньше, чтобы не нарушать функционирование всей системы.

Показатели значимости для нейрона с дифференцируемым нелинейным элементом

Эти показатели ищутся почти так же как для сумматора. Пусть

тогда

В евклидовой норме (что соответствует методу наименьших квадратов) получаем:

т.е. произведение модуля параметра

на среднеквадратичное отклонение с весами. Роль веса играет квадрат производной функции в точке .

Показатели значимости для нейрона с пороговым нелинейным элементом (персептрона)

Эти показатели требуют для своего вычисления еще одного эвристического хода, т.к. прямо воспользоваться предыдущими формулами невозможно. Пусть функция, вычисляемая нейроном, имеет вид

Для каждого вектора данных

необходимо оценить значимость изменения аргумента функции при замене на . Значение меняется только тогда, когда меняет знак, поэтому естественно оценивать значимость изменения переменной в масштабе, определенном текущем значением переменной, т.е. значимость оценивается, как . Из этого эвристического рассуждения получаем:

Если положить

и воспользоваться евклидовой мерой, то вновь получим произведение модуля параметров на среднеквадратичное отклонение с весом. В качестве весов выступают квадраты величин, обратных выходным сигналам сумматоров:

Полученные выражение для показателей значимости позволяют уп\-рощать основные элементы НС "снизу вверх", начиная с исключения самых малозначимых параметров.

Рекурсивное контрастирование и бинаризация

Рекурсивное контрастирование состоит в модификации параметров системы - одного за другим. Для этого параметры должны быть как-то линейно упорядочены

. При модификации

используются модифицированные значения

и немодифицированные .

Пусть для сумматора задана обучающая выборка входных векторов

и соответствующих выходных сигналов , а также известны значения параметров, которые реализуют сумматор: . Требуется произвести бинаризацию сумматора, т.е. найти числа и вектор с координатами или , чтобы значения функции на выборке как можно меньше отличались от . Критерием такого отличия будем считать . Построим координаты вектора по порядку

Пусть построены

. Обозначим (последние координат - нули), (последние координат - нули), (первые

координат - нули).

Введем функции:

Определим параметры

из условий , минимизируя функции и . Пусть и . Если , то полагаем , в противном случае .

После того как построены все

(

- размерность вектора данных), автоматически определяются и : если , то полагаем , , иначе .

Если бинаризация проведена, а необходимая точность не достигнута, то можно построить второй бинаризованный сумматор, корректирующий ошибку первого --- так, чтобы в сумме они хорошо аппроксимировали работу исходного сумматора на элементах обучающей выборки. В описанной процедуре делаем замену

и для этих исходных данных вновь строим бинаризованный сумматор по алгоритму рекурсивной бинаризации. Повторяем такое построение, пока не будет достигнута удовлетворительная точность. В результате получим набор бинаризованных сумматоров, которые в совокупности (т.е. в результате суммирования выходных сигналов) достаточно точно аппроксимируют исходный. При появлении весов, определяющих значимость отдельных примеров из обучающей выборки, рекурсивная бинаризация проводится точно так же, только в функциях появляются веса.

Если требуется тем же путем упростить любой другой элемент, линейный по параметрам,

, то вместо обучающей выборки берем семейство векторов с координатами . После такого

преобразования рассматриваемый элемент превращается в обычный сумматор, для которого последовательность действий уже описана.

Сокращение числа выходов в адаптивном линейном сумматоре (путь "снизу вверх")

Рассмотрим адаптивный линейный сумматор, вычисляющий линейную функцию

.

Решим задачу о сокращении числа выходных сигналов. Рассмотрим определение значимости по изменению выходного сигнала. Заметим, что:

Уничтожить

-й выходной сигнал можно двумя способами:

заменой параметра

на 0;заменой на постоянную величину не зависящую от .

В последнем случае получаем новую функцию

Такое преобразование означает, что одновременно с уничтожением

-й выходной связи приобретает новое значение:

При этом можно добиться меньшего изменения

, чем просто при приравнивании к нулю. Поэтому остановимся на замене -го выходного сигнала на постоянную величину . Значение этой постоянной определим исходя из минимизации изменения . Минимизация этого изменения, вычисленного в евклидовой норме, дает:

Таким образом, оптимальной является замена

на его среднее значение по исходной выборке. В обозначениях теории вероятностей:

где

- среднеквадратичное отклонение от на выборке .

Значимость замены оценивается как

При исключении сигналов по одному, они сортируются в соответствии со значениями

и отбрасываются (заменяются средним) сначала те, что соответствуют меньшим . Заметим, что поэтому путь "снизу вверх" универсален, но не оптимален. В частности, для сумматоров и других элементов, линейных по параметрам (например, квадратичных сумматоров), существует учитывающий все корреляции путь исключения "сверху вниз" с ортогонализацией. Далее ограничимся оценкой значимости по изменению выходного сигнала.

Сокращение описания "сверху вниз" - набор достаточного семейства наиболее значимых параметров

Метод исключения параметров "сверху вниз" с ортогонализацией применим не ко всяким функциям

, а только к таким, которые имеют вид:

Достоинство метода - автоматический учет корреляции между

. Рассмотрим устройства, вычисляющие функции

К ним относятся линейные сумматоры, квадратичные сумматоры и др.

Пусть заданы векторы данных:

Поставим задачу сокращения описания следующим образом: так определить некоторое наименьшее возможное множество индексов

и набор чисел , чтобы норма отклонения , где , не превышала некоторой наперед заданной величины. Все функции рассматриваются на конечном множестве . Для любой функции евклидова норма:

С каждой функцией

связан -мерный вектор с компонентами . Вектор с координатами является линейной комбинацией векторов с координатами . Линейную оболочку семейства векторов обозначим . Построим в пространстве ортонормированный базис с помощью последовательной ортогонализации векторов . Каждый следующий шаг ортогонализации выполним так, чтобы величина проекции на новый вектор базиса была максимальной из возможных. Процесс ортогонализации продолжим, пока , где - проекция на построенную ортогональную систему. По окончании процесса полагаем .

Полагаем . Тогда . Это и есть решение задачи. Числа выражаются через коэффициенты разложения векторов по и скалярные произведения : если , то .

Разложение по имеет рекурсивную форму:



Для функций вида с дифференцируемой функцией процедура аналогична с точностью до замены скалярного произведения: используется скалярное произведение с весами , где . В этом скалярном произведении вычисляются все нормы и проводится ортогонализация.

Для функций с пороговой нелинейностью на выходе используем скалярное произведение с весами .

Описанная процедура сокращения "сверху вниз" с ортогонализацией особенно важна для упрощения элементов сложных сетей, в структуре которых и вектор входных сигналов элемента может быть далек от исходных данных, и его выходной сигнал далек от оцениваемого выхода всей сложной системы.

Процедуры анализа значимости и сокращения описания выделяют наиболее важные параметры и связи в НС. По аналогии с обработкой изображения их называют процедурами контрастирования или редукции.

Роль контрастирования (редукции) не сводится только к сокращению описания: более общая задача - привести параметры системы к выделенному набору значений, в частности, уменьшить разрядность, что важно для удешевления специализированных устройств, экономии памяти и т.д.

Значимость параметров и сигналов. Сокращение описания (контрастирование) сетей.

Сокращение множества параметров и входных сигналов обученной нейронной сети преследует цели:

упрощение специализированных устройств;сокращение объема используемой памяти и увеличение быстродействия;удешевление сбора данных;обеспечение (или облегчение) интерпретации результатов обработки данных.

Существует два способа сокращения (редукции) описания:

редукция "снизу вверх" - постепенное удаление параметров от наименее значимых к более значимым;редукция "сверху вниз" - выделение наиболее значимых параметров и постепенное дополнение их менее значимыми.

Способ редукции "снизу вверх":

определяются наименее значимые параметры и устраняются вместе с соответствующими элементами системы;оставшиеся параметры модифицируются так, чтобы наилучшим способом решить задачу;циклически повторять пп. 1-2 до тех пор, пока задача не будет решаться с удовлетворительной точностью.

Голографические корреляторы

В голографических корреляторах образцы изображений запоминаются в виде голограммы (плоской или объемной) и восстанавливаются при когерентном освещении в петле обратной связи.

Входное изображение (возможно, зашумленное или неполное) коррелируется оптически одновременно со всеми запомненными изображениями. Корреляции обрабатываются пороговой функцией и подаются на вход системы, где наиболее сильные корреляции усиливают (и, возможно, корректируют или завершают) входное изображение. Этот процесс повторяется многократно, и усиленное изображение при каждом проходе изменяется, пока система не стабилизируется на требуемом изображении.

Оптические нейронные сети предлагают огромные выгоды с точки зрения скорости и плотности внутренних связей. Они могут быть использованы (в той или иной форме) для реализации сетей фактически с любой архитектурой.

В настоящее время ограничения электронно-оптических устройств создают множество серьезных проблем, которые должны быть решены прежде, чем оптические нейронные сети получат широкое применение. Однако, учитывая, что большое количество превосходных исследователей работает над этой проблемой, а также большую поддержку со стороны военных, можно надеяться на быстрый прогресс в этой области.

Электронная реализация нейронных сетей

В качестве единицы производительности нейросетей принято "число соединений в секунду" - CPS (connections per second). Под соединением здесь понимается умножение входного сигнала на весовой коэффициент и сложение с накопленной суммой.

Анализ нейросетевых алгоритмов позволяет сделать следующие выводы:

При решении плохо формализованных задач моделирования, прогнозирования и распознавания, которые обычно сводятся к конструированию областей многомерного пространства, достаточно малоразрядных представлений входов и весов и операций с фиксированной точкой. Это обусловлено тем, что входные сигналы нормируются и количество их значений невелико.При решении хорошо формализованных задач (например, задач комбинаторной оптимизации) существенна точность вычислений, что требует полноразрядных представлений чисел и операций с плавающей точкой.

Электронные нейронные сети обычно используются в качестве акселераторов для персональных ЭВМ при решении соответствующих классов задач (обработки сигналов и изображений, распознавания образов и т.п.).

Нейрочипы

Нейрочипы подразделяются на цифровые, аналоговые и гибридные. Они могут включать в себя схемы настройки весов при обучении или предусматривать внешнюю загрузку весов. Наибольшую проблему при создании нейрочипов представляют схемы умножения, так как именно они лимитируют скорость вычислений.

Аналоговые реализации используют простые физические эффекты для выполнения нейросетевых преобразований. Обеспечение заданной точности требует тщательного проектирования и изготовления.

Гибридные нейрочипы используют комбинацию аналогового и цифрового подходов. Например, входы могут быть аналоговыми, веса могут загружаться как цифровые и выходы могут быть цифровыми. Существуют нейрочипы, в которых используется представление данных частотой или шириной импульсов.

и векторный процессор для обработки

Отечественный нейропроцессор NM6403, разработанный в НПО "Модуль" (www.module.ru), имеет скалярный процессор (скалярное RISC-ядро) и векторный процессор для обработки двоичных векторов произвольной разрядности в пределах 1-64 битов. Скалярный процессор выполняет всю подготовку данных для работы векторного процессора.

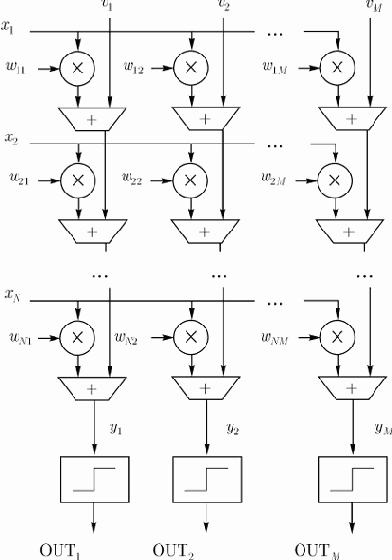
Модель слоя нейронов, эмулируемого процессором NM6403, показана на рис. 1. В общем случае слой имеет входов и состоит из

нейронов. -й нейрон выполняет операцию умножения - накопления над данными , поданными на соответствующие входы нейрона.

Нейропроцессор NM6403 имеет два встроенных линка, совместимых с линками сигнального микропроцессора TMS320C40. Кроме того, интерфейсы локальной и глобальной памятей позволяют без дополнительного оборудования подсоединять два нейропроцессора к общему блоку памяти.


увеличить изображение
Рис. 1.  Модель слоя нейронов

Мультипроцессорная система (рис. 2) из нейропроцессоров NM6403 эмулирует нейронную сеть в раз быстрее, чем один нейропроцессор.


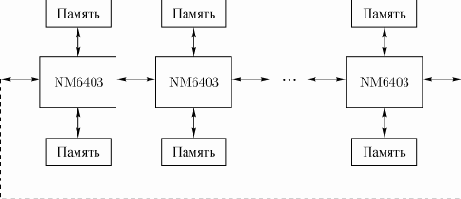
Рис. 2.  Линейная (кольцевая) система из нейропроцессоров NM6403

Оптическая реализация нейронных сетей

Мощность нейронной сети определяется большим количеством связей: отдельные элементы имеют относительно малые вычислительные мощности. Обеспечение требуемой связности в электронных цепях остается серьезной проблемой, особенно при реализации нейронных сетей с полным графом соединений. Электронные интегральные цепи являются существенно планарными с рельефностью, обусловленной множеством слоев.

Проблему связей можно решить при использовании оптических систем для реализации НС. Взаимное соединение нейронов с помощью световых лучей не требует изоляции между сигнальными путями: световые потоки могут пересекаться, не влияя друг на друга, и сигнальные пути могут располагаться в трех измерениях. Плотность путей передачи ограничена только размерами источников и детекторов. Все сигнальные пути могут работать одновременно, тем самым обеспечивая огромную скорость передачи данных.

В оптических НС величины оптических весов могут запоминаться в голограммах с высокой степенью плотности (до

бит на куб. см.). Веса могут модифицироваться в процессе работы сети.

К сожалению, возникает множество практических проблем при попытках оптической реализации нейронных сетей. Оптические устройства имеют собственные физические характеристики, часто не соответствующие требованиям искусственных нейронных сетей. Хотя они в действительности пригодны для обработки изображений, все же изображения от оптических нейронных сетей, полученные до настоящего времени, были разочаровывающе плохими. Однако достаточно взглянуть на первые пробы телевизионных передач, чтобы понять, какой огромный прогресс возможен в повышении качества изображения. Несмотря на эти трудности, а также на такие проблемы, как стоимость, размеры и критичность к ориентации, потенциальные возможности оптических систем побуждают попытки проведения интенсивных и широких исследований. В этой области происходят стремительные изменения, и в ближайшее время ожидаются важные улучшения.

Конфигурации оптических НС в основном подразделяются на две категории: векторно-матричные умножители и голографические корреляторы.

Векторно-матричные умножители

В качестве матрицы весов (рис. 3) используется фотопленка, у которой прозрачность каждого квадрата пропорциональна весу. Выход каждого фотодетектора является сверткой между входным вектором и соответствующим столбцом матрицы весов. Умножение выполняется параллельно. При использовании соответствующих высокоскоростных светодиодов и фотодетекторов умножение вектора на матрицу может быть выполнено менее, чем за наносекунду. Более того, скорость умножения практически не зависит от размерности массива. Это позволяет наращивать сети без существенного увеличения времени вычислений. Возможность менять веса основана на использовании жидкокристаллического клапана вместо фотографического негатива.

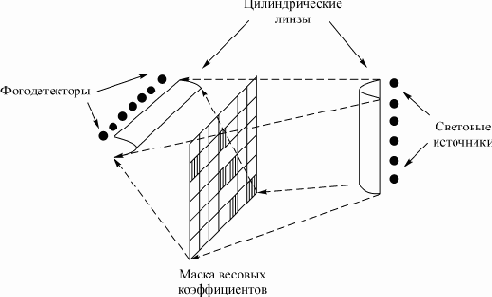
Рис. 3.  Электронно-оптический векторно-матричный умножитель

---

---