ПЕРСЕПТРОНЫ И ЗАРОЖДЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
В качестве научного предмета искусственные нейронные сети впервые заявили о себе в 40-е годы. Стремясь воспроизвести функции человеческого мозга, исследователи создали простые аппаратные (а позже программные) модели биологического нейрона и системы его соединений. Когда нейрофизиологи достигли более глубокого понимания нервной системы человека, эти ранние попытки стали восприниматься как весьма грубые аппроксимации. Тем не менее на этом пути были достигнуты впечатляющие результаты, стимулировавшие дальнейшие исследования, приведшие к созданию более изощренных сетей.

Рис.2.1. Персептронный нейрон
Первое систематическое изучение искусственных нейронных сетей было предпринято Маккалокком и Питтсом в 1943 г. [I]. Позднее в работе [3] они исследовали сетевые парадигмы для распознавания изображений, подвергаемых сдвигам и поворотам. Простая нейронная модель, показанная на рис. 2.1, использовалась в большей части их работы. Элемент ? умножает каждый вход х на вес
w и суммирует взвешенные входы. Если эта сумма больше заданного порогового значения, выход равен единице, в противном случае – нулю. Эти системы (и множество им подобных) получили название персептронов.
Они состоят из одного слоя искусственных нейронов, соединенных с помощью весовых коэффициентов с множеством входов (см. рис. 2.2), хотя в принципе описываются и более сложные системы.
В 60-е годы персептроны вызвали большой интерес и оптимизм. Розенблатт [4] доказал замечательную теорему об обучении персептронов, объясняемую ниже. Уидроу [5-8] дал ряд убедительных демонстраций систем персептронного типа, и исследователи во всем мире стремились изучить возможности этих систем. Первоначальная эйфория сменилась разочарованием, когда оказалось, что персептроны не способны обучиться решению ряда простых задач. Минский [2] строго проанализировал эту проблему и показал, что имеются жесткие ограничения на то, что могут выполнять однослойные персептроны, и, следовательно, на то, чему они могут обучаться.
Так как в то время методы обучения многослойных сетей не были известны, исследователи перешли в более многообещающие области, и исследования в области нейронных сетей пришли в упадок. Недавнее открытие методов обучения многослойных сетей в большей степени, чем какой-либо иной фактор, повлияло на возрождение интереса и исследовательских усилий.

Рис. 2.2. Персептрон со многими выходами
Работа Минского, возможно, и охладила пыл энтузиастов персептрона, но обеспечила время для необходимой консолидации и развития лежащей в основе теории. Важно отметить, что анализ Минского не был опровергнут. Он остается важным исследованием и должен изучаться, чтобы ошибки 60-х годов не повторились.
Несмотря на свои ограничения персептроны широко изучались (хотя не слишком широко использовались). Теория персептронов является основой для многих других типов искусственных нейронных сетей, и персептроны иллюстрируют важные принципы. В силу этих причин они являются логической исходной точкой для изучения искусственных нейронных сетей.
ПЕРСПЕКТИВЫ НА БУДУЩЕЕ
Искусственные нейронные сети предложены для задач, простирающихся от управления боем до присмотра за ребенком. Потенциальными приложениями являются те, где человеческий интеллект малоэффективен, а обычные вычисления трудоемки или неадекватны. Этот класс приложений во всяком случае не меньше класса, обслуживаемого обычными вычислениями, и можно предполагать, что искусственные нейронные сети займут свое место наряду с обычными вычислениями в качестве дополнения такого же объема и важности.
ПОЧЕМУ ИМЕННО ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ?
После двух десятилетий почти полного забвения интерес к искусственным нейронным сетям быстро вырос за последние несколько лет. Специалисты из таких далеких областей, как техническое конструирование, философия, физиология и психология, заинтригованы возможностями, предоставляемыми этой технологией, и ищут приложения им внутри своих дисциплин.
Это возрождение интереса было вызвано как теоретическими, так и прикладными достижениями. Неожиданно открылись возможности использования вычислений в сферах, до этого относящихся лишь к области человеческого интеллекта, возможности создания машин, способность которых учиться и запоминать удивительным образом напоминает мыслительные процессы человека, и наполнения новым значительным содержанием критиковавшегося термина «искусственный интеллект».
Что такое искусственные нейронные сети?
Что такое искусственные нейронные сети? Что они могут делать? Как они работают? Как их можно использовать? Эти и множество подобных вопросов задают специалисты из разных областей. Найти вразумительный ответ нелегко. Университетских курсов мало, семинары слишком дороги, а соответствующая литература слишком обширна и специализированна. Готовящиеся к печати превосходные книги могут обескуражить начинающих. Часто написанные на техническом жаргоне, многие из них предполагают свободное владение разделами высшей математики, редко используемыми в других областях.
Эта книга является систематизированным вводным курсом для профессионалов, не специализирующихся в математике. Все важные понятия формулируются сначала обычным языком. Математические выкладки используются, если они делают изложение более ясным. В конце глав помещены сложные выводы и доказательства, а также приводятся ссылки на другие работы. Эти ссылки составляют обширную библиографию важнейших работ в областях, связанных с искусственными нейронными сетями. Такой многоуровневый подход не только предоставляет читателю обзор по искусственным нейронным сетям, но также позволяет заинтересованным лицам серьезнее и глубже изучить предмет.
Значительные усилия были приложены, чтобы сделать книгу понятной и без чрезмерного упрощения материала. Читателям, пожелавшим продолжить более углубленное теоретическое изучение, не придется переучиваться. При упрощенном изложении даются ссылки на более подробные работы.
Книгу не обязательно читать от начала до конца. Каждая глава предполагается замкнутой, поэтому для понимания достаточно лишь знакомства с содержанием гл.1 и 2. Хотя некоторое повторение материала неизбежно, большинству читателей это не будет обременительно.
Книга имеет практическую направленность. Если главы внимательно изучены, то большую часть сетей оказывается возможным реализовать на обычном компьютере общего назначения. Читателю настоятельно рекомендуется так и поступать. Никакой другой метод не позволит добиться столь же глубокого понимания.
ПРЕДОСТЕРЕЖЕНИЕ
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Длительное время обучения может быть результатом неоптимального выбора длины шага. Неудачи в обучении обычно возникают по двум причинам: паралича сети и попадания в локальный минимум.
Предварительная обработка входных векторов
Весьма желательно (хотя и не обязательно) нормализовать входные векторы перед тем, как предъявлять их сети. Это выполняется с помощью деления каждой компоненты входного вектора на длину вектора. Эта длина находится извлечением квадратного корня из суммы квадратов компонент вектора. В алгебраической записи

Это превращает входной вектор в единичный вектор с тем же самым направлением, т.е. в вектор единичной длины в n-мерном пространстве.
Уравнение (4.6) обобщает хорошо известный случай двух измерений, когда длина вектора равна гипотенузе прямоугольного треугольника, образованного его х и у компонентами, как это следует из известной теоремы Пифагора. На рис. 4.2а такой двумерный вектор V представлен в координатах х-у, причем координата х равна четырем, а координата y – трем. Квадратный корень из суммы квадратов этих компонент равен пяти. Деление каждой компоненты V
на пять дает вектор V с компонентами 4/5 и 3/5, где V’ указывает в том же направлении, что и V, но имеет единичную длину.
На рис. 4.26 показано несколько единичных векторов. Они оканчиваются в точках единичной окружности (окружности единичного радиуса), что имеет место, когда у сети лишь два входа. В случае трех входов векторы представлялись бы стрелками, оканчивающимися на поверхности единичной сферы. Эти представления могут быть перенесены на сети, имеющие произвольное число входов, где каждый входной вектор является стрелкой, оканчивающейся на поверхности единичной гиперсферы (полезной абстракцией, хотя и не допускающей непосредственной визуализации).

Рис. 4.2а. Единичный входной вектор

Рис. 4.26. Двумерные единичные векторы на единичной окружности
При обучении слоя Кохонена на вход подается входной вектор и вычисляются его скалярные произведения с векторами весов, связанными со всеми нейронами Кохонена. Нейрон с максимальным значением скалярного произведения объявляется «победителем» и его веса подстраиваются.
Так как скалярное произведение, используемое для вычисления величин NET, является мерой сходства между входным вектором и вектором весов, то процесс обучения состоит в выборе нейрона Кохонена с весовым вектором, наиболее близким к входному вектору, и дальнейшем приближении весового вектора к входному. Снова отметим, что процесс является самообучением, выполняемым без учителя. Сеть самоорганизуется таким образом, что данный нейрон Кохонена имеет максимальный выход для данного входного вектора. Уравнение, описывающее процесс обучения имеет следующий вид:
wн = wс + a(x
– wс), (4.7)
где wн – новое значение веса, соединяющего входную компоненту х
с выигравшим нейроном; wс
– предыдущее значение этого веса; a – коэффициент скорости обучения, который может варьироваться в процессе обучения.
Каждый вес, связанный с выигравшим нейроном Кохонена, изменяется пропорционально разности между его величиной и величиной входа, к которому он присоединен. Направление изменения минимизирует разность между весом и его входом.
На рис. 4.3 этот процесс показан геометрически в двумерном виде. Сначала находится вектор
X – Wс, для этого проводится отрезок из конца W
в конец X. Затем этот вектор укорачивается умножением его на скалярную величину a, меньшую единицы, в результате чего получается вектор изменения ?. Окончательно новый весовой вектор Wн является отрезком, направленным из начала координат в конец вектора ?. Отсюда можно видеть, что эффект обучения состоит во вращении весового вектора в направлении входного вектора без существенного изменения его длины.

Рис. 4.3. Вращение весового вектора в процессе обучения (Wн – вектор новых весовых коэффициентов, Wс – вектор старых весовых коэффициентов)
Переменная к является коэффициентом скорости обучения, который вначале обычно равен ~ 0,7 и может постепенно уменьшаться в процессе обучения. Это позволяет делать большие начальные шаги для быстрого грубого обучения и меньшие шаги при подходе к окончательной величине.
Если бы с каждым нейроном Кохонена ассоциировался один входной вектор, то слой Кохонена мог бы быть обучен с помощью одного вычисления на вес. Веса нейрона-победителя приравнивались бы к компонентам обучающего вектора (a = 1). Как правило, обучающее множество включает много сходных между собой входных векторов, и сеть должна быть обучена активировать один и тот же нейрон Кохонена для каждого из них. В этом случае веса .этого нейрона должны получаться усреднением входных векторов, которые должны его активировать. Постепенное уменьшение величины a
уменьшает воздействие каждого обучающего шага, так что окончательное значение будет средней величиной от входных векторов, на которых происходит обучение. Таким образом, веса, ассоциированные с нейроном, примут значение вблизи «центра» входных векторов, для которых данный нейрон является «победителем».
Преодоление ограничения линейной разделимости
К концу 60-х годов проблема линейной разделимости была хорошо понята. К тому же было известно, что это серьезное ограничение представляемости однослойными сетями можно преодолеть, добавив дополнительные слои. Например, двухслойные сети можно получить каскадным соединением двух однослойных сетей. Они способны выполнять более общие классификации, отделяя те точки, которые содержатся в выпуклых ограниченных или неограниченных областях. Область называется выпуклой, если для любых двух ее точек соединяющий их отрезок целиком лежит в области. Область называется ограниченной, если ее можно заключить в некоторый круг. Неограниченную область невозможно заключить внутрь круга (например, область между двумя параллельными линиями). Примеры выпуклых ограниченных и неограниченных областей представлены на рис.2.7.
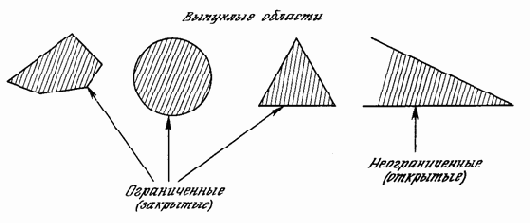
Рис. 1.7. Выпуклые ограниченные и неограниченные области
Чтобы уточнить требование выпуклости, рассмотрим простую двухслойную сеть с двумя входами, подведенными к двум нейронам первого слоя, соединенными с единственным нейроном в слое 2 (см. рис. 2.8). Пусть порог выходного нейрона равен 0,75, а оба его веса равны 0,5. В этом случае для того, чтобы порог был превышен и на выходе появилась единица, требуется, чтобы оба нейрона первого уровня на выходе имели единицу. Таким образом, выходной нейрон реализует логическую функцию И. На рис. 2.8 каждый нейрон слоя 1 разбивает плоскость х-у на две полуплоскости, один обеспечивает единичный выход для входов ниже верхней линии, другой – для входов выше нижней линии. На рис. 2.8 показан результат такого двойного разбиения, где выходной сигнал нейрона второго слоя равен единице только внутри V-образной области. Аналогично во втором слое может быть использовано три нейрона с дальнейшим разбиением плоскости и созданием области треугольной формы. Включением достаточного числа нейронов во входной слой может быть образован выпуклый многоугольник любой желаемой формы. Так как они образованы с помощью операции И над областями, задаваемыми линиями, то все такие многогранники выпуклы, следовательно, только выпуклые области и возникают.
Точки, не составляющие выпуклой области, не могут быть отделены от других точек плоскости двухслойной сетью.

Рис. 1.8. Выпуклая область решений, задаваемая двухслойной сетью
Нейрон второго слоя не ограничен функцией И. Он может реализовывать многие другие функции при подходящем выборе весов и порога. Например, можно сделать так, чтобы единичный выход любого из нейронов первого слоя приводил к появлению единицы на выходе нейрона второго слоя, реализовав тем самым логическое ИЛИ. Имеется 16 двоичных функций от двух переменных. Если выбирать подходящим образом веса и порог, то можно воспроизвести 14 из них (все, кроме ИСКЛЮЧАЮЩЕЕ ИЛИ и ИСКЛЮЧАЮЩЕЕ НЕТ).
|
ограниченной многоугольной областью. Поэтому для разделения плоскостей P и Q необходимо, чтобы все P лежали внутри выпуклой многоугольной области, не содержащей точек Q (или наоборот).

Рис. 2.9. «Вогнутая» область решений, задаваемая трехслойной сетью
Трехслойная сеть, однако, является более общей. Ее классифицирующие возможности ограничены лишь числом искусственных нейронов и весов. Ограничения на выпуклость отсутствуют. Теперь нейрон третьего слоя принимает в качестве входа набор выпуклых многоугольников, и их логическая комбинация может быть невыпуклой. На рис. 2.9 иллюстрируется случай, когда два треугольника A и B, скомбинированные с помощью функций «A и не B», задают невыпуклую область. При добавлении нейронов и весов число сторон многоугольников может неограниченно возрастать. Это позволяет аппроксимировать область любой формы с любой точностью.Вдобавок не все выходные области второго слоя должны пересекаться. Возможно, следовательно, объединять различные области, выпуклые и невыпуклые, выдавая на выходе единицу всякий раз, когда входной вектор принадлежит одной из них.
Несмотря на то что возможности многослойных сетей были известны давно, в течение многих лет не было теоретически обоснованного алгоритма для настройки их весов. В последующих главах мы детально изучим многослойные обучающие алгоритмы, но сейчас достаточно понимать проблему и знать, что исследования привели к определенным результатом.
Преодоление сетевого паралича
Очевидное решение, состоящее в ограничении диапазона изменения весовых шагов, ставит вопрос о математической корректности полученного таким образом алгоритма. В работе [6] доказана сходимость системы к глобальному минимуму лишь для исходного алгоритма. Подобного доказательства при искусственном ограничении размера шага не существует. В действительности экспериментально выявлены случаи, когда для реализации некоторой функции требуются большие веса, и два больших веса, вычитаясь, дают малую разность.
Другое решение состоит в рандомизации весов тех нейронов, которые оказались в состоянии насыщения. Недостатком его является то, что оно может серьезно нарушить обучающий процесс, иногда затягивая его до бесконечности.
Для решения проблемы паралича был найден метод, не нарушающий достигнутого обучения. Насыщенные нейроны выявляются с помощью измерения их сигналов OUT. Когда величина OUT приближается к своему предельному значению, положительному или отрицательному, на веса, питающие этот нейрон, действует сжимающая функция. Она подобна используемой для получения нейронного сигнала OUT, за исключением того, что диапазоном ее изменения является интервал (+5,–5) или другое подходящее множество. Тогда модифицированные весовые значения равны

Эта функция сильно уменьшает величину очень больших весов, воздействие на малые веса значительно более слабое. Далее она поддерживает симметрию, сохраняя небольшие различия между большими весами. Экспериментально было показано, что эта функция выводит нейроны из состояния насыщения без нарушения достигнутого в сети обучения. Не было затрачено серьезных усилий для оптимизации используемой функции, другие значения констант могут оказаться лучшими.
Экспериментальное результаты. Комбинированный алгоритм, использующий обратное распространение и обучение Коши, применялся для обучения нескольких больших сетей. Например, этим методом была успешно обучена система, распознающая рукописные китайские иероглифы [б].
Все же время обучения может оказаться большим (приблизительно 36часов машинного времени уходило на обучение).
В другом эксперименте эта сеть обучалась на задаче ИСКЛЮЧАЮЩЕЕ ИЛИ, которая была использована в качестве теста для сравнения с другими алгоритмами. Для сходимости сети в среднем требовалось около 76 предъявлении обучающего множества. В качестве сравнения можно указать, что при использовании обратного распространения в среднем требовалось около 245 предъявлении для решения этой же задачи [5] и 4986 итераций при использовании обратного распространения второго порядка.
Ни одно из обучений не привело к локальному минимуму, о которых сообщалось в [5]. Более того, ни одно из 160 обучений не обнаружило неожиданных патологий, сеть всегда правильно обучалась.
Эксперименты же с чистой машиной Коши привели к значительно большим временам обучения. Например, при r
= 0,002 для обучения сети в среднем требовалось около 2284 предъявлении обучающего множества.
Б. Алгоритмы обучения
Искусственные нейронные сети обучаются самыми разнообразными методами. К счастью, большинство методов обучения исходят из общих предпосылок и имеет много идентичных характеристик. Целью данного приложения является обзор некоторых фундаментальных алгоритмов, как с точки зрения их текущей применимости, так и с точки зрения их исторической важности. После ознакомления с этими фундаментальными алгоритмами другие, основанные на них, алгоритмы будут достаточно легки для понимания и новые разработки также могут быть лучше поняты и развиты.
СЖАТИЕ ДАННЫХ
В дополнение к обычным функциям отображения векторов встречное распространение оказывается полезным и в некоторых менее очевидных прикладных областях. Одним из наиболее интересных примеров является сжатие данных.
Сеть встречного распространения может быть использована для сжатия данных перед их передачей, уменьшая тем самым число битов, которые должны быть переданы. Допустим, что требуется передать некоторое изображение. Оно может быть разбито на подизображения S, как показано на рис. 4.5. Каждое подизображение разбито на пиксели (мельчайшие элементы изображения). Тогда каждое подизображение является вектором, элементами которого являются пиксели, из которых состоит подизображение. Допустим для простоты, что каждый пиксель – это единица (свет) или нуль (чернота). Если в подизображении имеется п пикселей, то для его передачи потребуется п бит. Если допустимы некоторые искажения, то для передачи типичного изображения требуется существенно меньшее число битов, что позволяет передавать изображения быстрее. Это возможно из-за статистического распределения векторов подизображений. Некоторые из них встречаются часто, тогда как другие встречаются так редко, что могут быть грубо аппроксимированы. Метод, называемый векторным квантованием, находит более короткие последовательности битов, наилучшим образом представляющие эти подизображения.

Рис. 4.5. Система сжатия изображений.
Сеть встречного распространения может быть использована для выполнения векторного квантования. Множество векторов подизображений используется в качестве входа для обучения слоя Кохонена по методу аккредитации, когда лишь выход одного нейрона равен 1. Веса слоя Гроссберга обучаются выдавать бинарный код номера того нейрона Кохонена, выход которого равен 1. Например, если выходной сигнал нейрона 7 равен 1 (а все остальные равны 0), то слой Гроссберга будет обучаться выдавать 00...000111 (двоичный код числа 7). Это и будет являться более короткой битовой последовательностью передаваемых символов.
На приемном конце идентичным образом обученная сеть встречного распространения принимает двоичный код и реализует обратную функцию, аппроксимирующую первоначальное подизображение.
Этот метод применялся как к речи, так и к изображениям, с коэффициентом сжатия данных от 10:1 до 100:1. Качество было ' приемлемым, хотя некоторые искажения данных на приемном конце неизбежны.
ПРИЛОЖЕНИЯ К ОБЩИМ НЕЛИНЕЙНЫМ ЗАДАЧАМ ОПТИМИЗАЦИИ
До сих пор в обсуждении предполагалось, что мы корректируем веса в традиционных искусственных нейронных сетях. Фактически, однако, это есть лишь некоторый частный случай. Эти статистические методы носят значительно более общий характер и способны решать множество задач нелинейной оптимизации.
Нелинейная оптимизационная задача
включает множество независимых переменных, детерминистским образом связанных с значением целевой функции. Целью является нахождение такого множества значений независимых переменных, которое минимизирует (или максимизирует) целевую функцию. Рассмотрим, например, нахождение минимума функции F{x) = 3х3 + 6х2 – 2х + 3.
Здесь имеется единственная независимая переменная х,
управляющая значением целевой функции F(x),
которая должна быть минимизирована. Эта простая функция легко минимизируется с помощью методов дифференциального исчисления, однако минимизировать подобным образом более сложные функции от большого числа переменных может оказаться затруднительным.
Во многих практических ситуациях функциональная связь между независимыми переменными и целевой функцией неизвестна и фактически не может быть известной. Сложный химический процесс может не иметь адекватной математической модели. Единственными измеряемыми величинами могут быть «выход», «качество», «цена» и т. д., которые являются неизвестными функциями от большого числа таких независимых переменных, как температура, время и характеристики сырья.
Подобная задача может решаться следующим образом:
1. Система наблюдается и собираются данные для составления обучающего множества. Каждый элемент обучающего множества состоит из замеров во время наблюдений и включает значения всех входов (входной вектор) и всех выходов (выходной вектор).
2. Сеть обучается на этом обучающем множестве. Обучение состоит из предъявления входного вектора, вычисления выходного вектора, сравнивания выходного вектора с входным вектором, полученным в процессе наблюдений, и коррекции весов, минимизирующей разность между ними.
Каждый входной вектор предъявляется по очереди, и сеть частично обучается. После большого числа предъявлении входных векторов сеть сойдется к решению, которое минимизирует разность между желаемыми и измеренными выходами системы. Фактически сеть строит внутреннюю модель неизвестной системы. Если обучающее множество достаточно велико, сеть сходится к точной модели системы. Если сети предъявить некоторый входной вектор, отличный от любого из векторов, предъявленных при обучении, то полностью обученная сеть выдаст тот же самый выходной вектор, что и настоящая система.
3. Максимизируется целевая функция. Целевая функция выходов должна быть сконструирована таким образом, чтобы выражать степень «удовлетворительности» результата. Теперь входы становятся переменными для обученной сети. Они подстраиваются с помощью того же самого обучающего алгоритма, который применялся для выставления весов на шаге 2, однако используются для максимизации целевой функции.
Во многих случаях могут присутствовать ограничения, накладываемые задачей. Например, может быть невозможно физически брать значения переменных вне некоторого диапазона. Эти ограничения (которые могут быть сложными выражениями) могут быть легко учтены отбрасыванием на шаге 3 любого изменения входной переменной, которое нарушает ограничение.
Это обобщение метода стохастической оптимизации позволяет его использовать для широкого круга оптимизационных задач. Можно применять и другие методы, но стохастический метод позволяет преодолеть трудности, обусловленные локальными минимумами, с которыми сталкивается метод обратного распространения и другие методы градиентного спуска. К сожалению, вероятностная природа процесса обучения может приводить к большому времени сходимости. Использование методов псевдотеплоемкости может существенно уменьшить это время, но процесс все равно остается медленным.
ПРИМЕНЕНИЯ
Обратное распространение было использовано в широкой сфере прикладных исследований. Некоторые из них описываются здесь, чтобы продемонстрировать мощь этого метода.
Фирма NEC в Японии объявила недавно, что обратное распространение было ею использовано для визуального распознавания букв, причем точность превысила 99%. Это улучшение было достигнуто с помощью комбинации обычных алгоритмов с сетью обратного распространения, обеспечивающей дополнительную проверку.
В работе [8] достигнут впечатляющий успех с Net-Talk, системой, которая превращает печатный английский текст в высококачественную речь. Магнитофонная запись процесса обучения сильно напоминает звуки ребенка на разных этапах обучения речи.
В [2] обратное распространение использовалось в машинном распознавании рукописных английских слов. Буквы, нормализованные по размеру, наносились на сетку, и брались проекции линий, пересекающих квадраты сетки. Эти проекции служили затем входами для сети обратного распространения. Сообщалось о точности 99,7% при использовании словарного фильтра.
В [3] сообщалось об успешном применении обратного распространения к сжатию изображений, когда образы представлялись одним битом на пиксель, что было восьмикратным улучшением по сравнению с входными данными.
Применимость
Искусственные нейронные сети не являются панацеей. Они, очевидно, не годятся для выполнения таких задач, как начисление заработной платы. Похоже, однако, что им будет отдаваться предпочтение в большом классе задач распознавания образов, с которыми плохо или вообще не справляются обычные компьютеры.
ПРИМЕР ОБУЧЕНИЯ СЕТИ APT
В общих чертах сеть обучается посредством изменения весов таким образом, что предъявление сети входного вектора заставляет сеть активизировать нейроны в слое распознавания, связанные с сходным запомненным вектором. Кроме этого, обучение проводится в форме, не разрушающей запомненные ранее образы, предотвращая тем самым временную нестабильность. Эта задача управляется на уровне выбора критерия сходства. Новый входной образ (который сеть не видела раньше) не будет соответствовать запомненным образам с точки зрения параметра сходства, тем самым формируя новый запоминаемый образ. Входной образ, в достаточной степени соответствующий одному из запомненных образов, не будет формировать нового экземпляра, он просто будет модифицировать тот, на который он похож. Таким образом при соответствующем выборе критерия сходства предотвращается запоминание ранее изученных образов и временная нестабильность.

Рис. 8.6. Процесс обучения APT
На рис. 8.6 показан типичный сеанс обучения сети APT. Буквы показаны состоящими из маленьких квадратов, каждая буква размерностью 8x8. Каждый квадрат в левой части представляет компоненту вектора Х с единичным значением, не показанные квадраты являются компонентами с нулевыми значениями. Буквы справа представляют запомненные образы, каждый является набором величин компонент вектора Тj.
Вначале на вход заново проинициированной системы подается буква «С». Так как отсутствуют запомненные образы, фаза поиска заканчивается неуспешно; новый нейрон выделяется в слое распознавания, и веса Тj
устанавливаются равными соответствующим компонентам входного вектора, при этом веса Вj
представляют масштабированную версию входного вектора.
Далее предъявляется буква «В». Она также вызывает неуспешное окончание фазы поиска и распределение нового нейрона. Аналогичный процесс повторяется для буквы «Е». Затем слабо искаженная версия буквы «Е» подается на вход сети. Она достаточно точно соответствует запомненной букве «Е», чтобы выдержать проверку на сходство, поэтому используется для обучения сети.
Отсутствующий пиксель в нижней ножке буквы «Е» устанавливает в 0 соответствующую компоненту вектора С, заставляя обучающий алгоритм установить этот вес запомненного образа в нуль, тем самым воспроизводя искажения в запомненном образе. Дополнительный изолированный квадрат не изменяет запомненного образа, так как не соответствует единице в запомненном образе.
Четвертым символом является буква «Е» с двумя различными искажениями. Она не соответствует ранее запомненному образу (S меньше чем r), поэтому для ее запоминания выделяется новый нейрон.
Этот пример иллюстрирует важность выбора корректного значения критерия сходства. Если значение критерия слишком велико, большинство образов не будут подтверждать сходство с ранее запомненными и сеть будет выделять новый нейрон для каждого из них. Это приводит к плохому обобщению в сети, в результате даже незначительные изменения одного образа будут создавать отдельные новые категории. Количество категорий увеличивается, все доступные нейроны распределяются, и способность системы к восприятию новых данных теряется. Наоборот, если критерий сходства слишком мал, сильно различающиеся образы будут группироваться вместе, искажая запомненный образ до тех пор, пока в результате не получится очень малое сходство с одним из них.
К сожалению, отсутствует теоретическое обоснование выбора критерия сходства, в каждом конкретном случае необходимо решить, какая степень сходства должна быть принята для отнесения образов к одной категории. Границы между категориями часто неясны, и решение задачи для большого набора входных векторов может быть чрезмерно трудным.
В работе [2] предложена процедура с использованием обратной связи для настройки коэффициента сходства, вносящая, однако, некоторые искажения в результате классификации как «наказание» за внешнее вмешательство с целью увеличения коэффициента сходства. Такие системы требуют правил определения, является ли производимая ими классификация корректной.
Проблема функции ИСКЛЮЧАЮЩЕЕ ИЛИ
Один из самых пессимистических результатов Минского показывает, что однослойный персептрон не может воспроизвести такую простую функцию, как ИСКЛЮЧАЮЩЕЕ ИЛИ. Это функция от двух аргументов, каждый из которых может быть нулем или единицей. Она принимает значение единицы, когда один из аргументов равен единице (но не оба). Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рис.2.4. Обозначим один вход через х, а другой через у, тогда все их возможные комбинации будут состоять из четырех точек на плоскости х-у, как показано на рис. 2.5. Например, точка х
= 0 и у = 0 обозначена на рисунке как точка А Табл. 2.1 показывает требуемую связь между входами и выходом, где входные комбинации, которые должны давать нулевой выход, помечены А0 и А1, единичный выход – В0 и В1.

Рис. 2.4. Однонейронная система
В сети на рис. 2.4 функция F
является обычным порогом, так что OUT принимает значение ноль, когда NET меньше 0,5, и единица в случае, когда NET больше или равно 0,5. Нейрон выполняет следующее вычисление:
NET = xw1 + yw2 (2.1)
Никакая комбинация значений двух весов не может дать соотношения между входом и выходом, задаваемого табл. 2.1. Чтобы понять это ограничение, зафиксируем NET на величине порога 0,5. Сеть в этом случае описывается уравнением (2.2). Это уравнение линейно по х
и у, т. е. все значения по х и у,
удовлетворяющие этому уравнению, будут лежать на некоторой прямой в плоскости х-у.
xw1 + yw2 = 0,5 (2.2)
Таблица 2.1.
Таблица истинности для функции ИСКЛЮЧАЮЩЕЕ ИЛИ
| Точки | Значения х | Значения у | Требуемый выход | ||||
| A0 | 0 | 0 | 0 | ||||
| B0 | 1 | 0 | 1 | ||||
| B1 | 0 | 1 | 1 | ||||
| A1 | 1 | 1 | 0 |
Любые входные значения для х и у на этой линии будут давать пороговое значение 0,5 для NET.
Входные значения с одной стороны прямой обеспечат значения NET больше порога, следовательно, OUT=1. Входные значения по другую сторону прямой обеспечат значения NET меньше порогового значения, делая OUT равным 0. Изменения значений w1, w2 и порога будут менять наклон и положение прямой. Для того чтобы сеть реализовала функцию ИСКЛЮЧАЮЩЕЕ ИЛИ, заданную табл. 2.1, нужно расположить прямую так, чтобы точки А были с одной стороны прямой, а точки В – с другой. Попытавшись нарисовать такую прямую на рис. 2.5, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции ИСКЛЮЧАЮЩЕЕ ИЛИ.

Рис. 2.5. Проблема ИСКЛЮЧАЮЩЕЕ ИЛИ
Взглянув на задачу с другой точки зрения, рассмотрим NET как поверхность над плоскостью х-у.
Каждая точка этой поверхности находится над соответствующей точкой плоскости х-у на расстоянии, равном значению NET в этой точке. Можно показать, что наклон этой NET-поверхности одинаков для всей поверхности х-у.
Все точки, в которых значение NET равно величине порога, проектируются на линию уровня плоскости NET (см. рис. 2.6).

Рис. 2.6. Персептронная NET-плоскость
Ясно, что все точки по одну сторону пороговой прямой спроецируются в значения NET, большие порога, а точки по другую сторону дадут меньшие значения NET. Таким образом, пороговая прямая разбивает плоскость х-у на две области. Во всех точках по одну сторону пороговой прямой значение OUT равно единице, по другую сторону – нулю.
ПРОЛОГ
В последующих главах представлены и проанализированы некоторые наиболее важные сетевые конфигурации и их алгоритмы обучения. Представленные парадигмы дают представление об искусстве конструирования сетей в целом, его прошлом и настоящем. Многие другие парадигмы при тщательном рассмотрении оказываются лишь их модификациями. Сегодняшнее развитие нейронных сетей скорее эволюционно, чем революционно. Поэтому понимание представленных в данной книге парадигм позволит следить за прогрессом в этой быстро развивающейся области.
Упор сделан на интуитивные и алгоритмические, а не математические аспекты. Книга адресована скорее пользователю искусственных нейронных сетей, чем теоретику. Сообщается, следовательно, достаточно информации, чтобы дать читателю возможность понимать основные идеи. Те, кто знаком с программированием, смогут реализовать любую из этих сетей. Сложные математические выкладки опущены, если только они не имеют прямого отношения к реализации сети. Для заинтересованного читателя приводятся ссылки на более строгие и полные работы.
Размер шага
Внимательный разбор доказательства сходимости в [7] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. В [11] описан адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения.
Режим интерполяции
До сих пор мы обсуждали алгоритм обучения, в котором для каждого входного вектора активировался лишь один нейрон Кохонена. Это называется методом аккредитации. Его точность ограничена, так как выход полностью является функцией лишь одного нейрона Кохонена.
В методе интерполяции
целая группа нейронов Кохонена, имеющих наибольшие выходы, может передавать свои выходные сигналы в слой Гроссберга. Число нейронов в такой группе должно выбираться в зависимости от задачи, и убедительных данных относительно оптимального размера группы не имеется. Как только группа определена, ее множество выходов NET рассматривается как вектор, длина которого нормализуется на единицу делением каждого значения NET на корень квадратный из суммы квадратов значений NET в группе. Все нейроны вне группы имеют нулевые выходы.
Метод интерполяции способен устанавливать более сложные соответствия и может давать более точные результаты. По-прежнему, однако, нет убедительных данных, позволяющих сравнить режимы интерполяции и аккредитации.
САМООРГАНИЗАЦИЯ
В работе [3] описывались интересные и полезные результаты исследований Кохонена на самоорганизующихся структурах, используемых для задач распознавания образов. Вообще эти структуры классифицируют образы, представленные векторными величинами, в которых каждый компонент вектора соответствует элементу образа. Алгоритмы Кохонена основываются на технике обучения без учителя. После обучения подача входного вектора из данного класса будет приводить к выработке возбуждающего уровня в каждом выходном нейроне; нейрон с максимальным возбуждением представляет классификацию. Так как обучение проводится без указания целевого вектора, то нет возможности определять заранее, какой нейрон будет соответствовать данному классу входных векторов. Тем не менее это планирование легко проводится путем тестирования сети после обучения.
Алгоритм трактует набор из n
входных весов нейрона как вектор в n-мерном пространстве. Перед обучением каждый компонент этого вектора весов инициализируется в случайную величину. Затем каждый вектор нормализуется в вектор с единичной длиной в пространстве весов. Это делается делением каждого случайного веса на квадратный корень из суммы квадратов компонент этого весового вектора.
Все входные вектора обучающего набора также нормализуются и сеть обучается согласно следующему алгоритму:
1. Вектор Х
подается на вход сети.
2. Определяются расстояния Dj (в n-мерном пространстве) между Х и весовыми векторами Wj
каждого нейрона. В евклидовом пространстве это расстояние вычисляется по следующей формуле

где хi
– компонента i
входного вектора X, wij
– вес входа i нейрона j.
3. Нейрон, который имеет весовой вектор, самый близкий к X, объявляется победителем. Этот весовой вектор, называемый Wc, становится основным в группе весовых векторов, которые лежат в пределах расстояния D от Wc.
4. Группа весовых векторов настраивается в соответствии со следующим выражением:
Wj(t+l) = Wj(t) + a[X – Wj(t)]
для всех весовых векторов в пределах расстояния D от Wc
5. Повторяются шаги с 1 по 4 для каждого входного вектора.
В процессе обучения нейронной сети значения D и a постепенно уменьшаются. Автор [3] рекомендовал, чтобы коэффициент a в начале обучения устанавливался приблизительно равным 1 и уменьшался в процессе обучения до 0, в то время как D может в начале обучения равняться максимальному расстоянию между весовыми векторами и в конце обучения стать настолько маленьким, что будет обучаться только один нейрон.
В соответствии с существующей точкой зрения, точность классификации будет улучшаться при дополнительном обучении. Согласно рекомендации Кохонена, для получения хорошей статистической точности количество обучающих циклов должно быть, по крайней мере, в 500 раз больше количества выходных нейронов.
Обучающий алгоритм настраивает весовые векторы в окрестности возбужденного нейрона таким образом, чтобы они были более похожими на входной вектор. Так как все векторы нормализуются в векторы с единичной длиной, они могут рассматриваться как точки на поверхности единичной гиперсферы. В процессе обучения группа соседних весовых точек перемещается ближе к точке входного вектора. Предполагается, что входные векторы фактически группируются в классы в соответствии с их положением в векторном пространстве. Определенный класс будет ассоциироваться с определенным нейроном, перемещая его весовой вектор в направлении центра класса и способствуя его возбуждению при появлении на входе любого вектора данного класса.
После обучения классификация выполняется посредством подачи на вход сети испытуемого вектора, вычисления возбуждения для каждого нейрона с последующим выбором нейрона с наивысшим возбуждением как индикатора правильной классификации.
СЕТЬ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ ПОЛНОСТЬЮ
На рис.4.4 показана сеть встречного распространения целиком. В режиме нормального функционирования предъявляются входные векторы Х и Y, и обученная сеть дает на выходе векторы X’ и Y’, являющиеся аппроксимациями соответственно для Х и Y. Векторы Х и Y
предполагаются здесь нормализованными единичными векторами, следовательно, порождаемые на выходе векторы также будут иметь тенденцию быть нормализованными.
В процессе обучения векторы Х и Y подаются одновременно и как входные векторы сети, и как желаемые выходные сигналы. Вектор Х используется для обучения выходов X’, а вектор Y – для обучения выходов Y’ слоя Гроссберга. Сеть встречного распространения целиком обучается с использованием того же самого метода, который описывался для сети прямого действия. Нейроны Кохонена принимают входные сигналы как от векторов X, так и от векторов Y. Но это неотличимо от ситуации, когда имеется один большой вектор, составленный из векторов Х и Y, и не влияет на алгоритм обучения.

Рис. 4.4. Полная сеть встречного распространения
В качестве результирующего получается единичное отображение, при котором предъявление пары входных векторов порождает их копии на выходе. Это не представляется особенно интересным, если не заметить, что предъявление только вектора Х (с вектором Y, равным нулю) порождает как выходы X’, так и выходы Y’. Если F – функция, отображающая Х в Y’, то сеть аппроксимирует ее. Также, если F обратима, то предъявление только вектора Y
(приравнивая Х нулю) порождает X’. Уникальная способность порождать функцию и обратную к ней делает сеть встречного распространения полезной в ряде приложений.
Рис. 4.4 в отличие от первоначальной конфигурации [5] не демонстрирует противоток в сети, по которому она получила свое название. Такая форма выбрана потому, что она также иллюстрирует сеть без обратных связей и позволяет обобщить понятия, развитые в предыдущих главах.
Сетевые конфигурации

Рис.3.1. Искусственный нейрон с активационнной функцией
Нейрон. На рис. 3.1 показан нейрон, используемый в качестве основного строительного блока в сетях обратного распространения. Подается множество входов, идущих либо извне, либо от предшествующего слоя. Каждый из них умножается на вес, и произведения суммируются. Эта сумма, обозначаемая NET, должна быть вычислена для каждого нейрона сети. После того, как величина NET вычислена, она модифицируется с помощью активационной функции и получается сигнал OUT.

Рис. 3.2. Сигмоидальная активационная функция.
На рис. 3.2 показана активационная функция, обычно используемая для обратного распространения.

Как показывает уравнение (3.2), эта функция, называемая сигмоидом,
весьма удобна, так как имеет простую производную, что используется при реализации алгоритма обратного распространения.

Сигмоид, который иногда называется также логистической,
или сжимающей функцией, сужает диапазон изменения NET так, что значение OUT лежит между нулем и единицей. Как указывалось выше, многослойные нейронные сети обладают большей представляющей мощностью, чем однослойные, только в случае присутствия нелинейности. Сжимающая функция обеспечивает требуемую нелинейность.
В действительности имеется множество функций, которые могли бы быть использованы. Для алгоритма обратного распространения требуется лишь, чтобы функция была всюду дифференцируема. Сигмоид удовлетворяет этому требованию. Его дополнительное преимущество состоит в автоматическом контроле усиления. Для слабых сигналов (величина NET близка к нулю) кривая вход-выход имеет сильный наклон, дающий большое усиление. Когда величина сигнала становится больше, усиление падает. Таким образом, большие сигналы воспринимаются сетью без насыщения, а слабые сигналы проходят по сети без чрезмерного ослабления.
Сети Хопфилда и машина Больцмана
Недостатком сетей Хопфилда является их тенденция стабилизироваться в локальном, а не глобальном минимуме функции энергии. Эта трудность преодолевается в основном с помощью класса сетей, известных под названием машин Больцмана, в которых изменения состояний нейронов обусловлены статистическими, а не детерминированными закономерностями. Существует тесная аналогия между этими методами и отжигом металла, поэтому и сами методы часто называют имитацией отжига.
Сети Хопфилда на базе электронно-оптических матричных умножителей
Если выходы фотодетекторов в сети подаются обратно для управления соответствующими световыми входами, реализуется электронно-оптическая сеть Хопфилда. Для выполнения этого должна быть обеспечена пороговая функция активации. В настоящее время функция активации наилучшим образом реализуется с помощью электронных цепей, следующих за каждым фотодетектором.
Для удовлетворения требований стабильности массив весов должен быть симметричным с нулевыми коэффициентами для квадратов главной диагонали (w11, w12, wmn).
Электронно-оптическая двунаправленная ассциативная память (ДАП). Если две системы, показанные на рис. 9.1, соединены в каскад (выход второй системы подается на вход первой), реализуется электронно-оптическая ДАП. Для обеспечения стабильности вторая весовая маска должна являться транспозицией первой.
В [9] описана компактная система, в которой для реализации электронно-оптической ДАП требуется только одна маска и оптическая система (рис. 9.2). Здесь каждые фотодетектор и световой источник заменяются парой фотодетектор
– световой источник. Функционирует данная система аналогично ранее описанному простому фотооптическому умножителю, за исключением того, что выход каждого фотодетектора управляется связанным с ним световым источником.
В процессе работы световой поток от каждого источника света справа проходит через цилиндрическую линзу, освещая соответствующую строку световой маски. Эта линза разворачивает световой поток в горизонтальном направлении, оставляя его неразвернутым в вертикальном направлении.
Каждый фотодетектор слева получает световой поток от столбца весовой маски и с помощью подключенных к нему электронных цепей реализует пороговую функцию для выработки электрического выходного сигнала NET. Сигнал NET затем управляет соответствующим данному фотодетектору световым источником, свет от которого проходит через оптическую подсистему, освещая тот же столбец. Следует отметить, что одно и то же оптическое пространство используется световыми образами, проходящими слева направо и справа налево.
Так как световые потоки не взаимодействуют между собой, это не вызывает проблем.

Рис. 9.2. Электронно-оптическая двунаправленная ассоциативная память
Каждый фотодетектор реагирует на световой поток от всей строки, его электронная часть реализует пороговую функцию и результирующий сигнал управляет связанным с ним световым источником. Тем самым замыкается петля обратной связи, включающая световые источники, фотодетекторы и оптическую систему. Заметим, что устойчивость ДАП гарантируется, даже если матрица не симметрична; кроме того, не требуется обязательного равенства нулю элементов главной диагонали.
Массивы линейных модуляторов. Линейный модулятор, недостаточно изученное до настоящего времени устройство, позволяет надеяться на существенное упрощение структуры электронно-оптических сетей. Как показано на рис. 9.3, линейный модулятор представляет собой тонкую пластину с чередующимися полосками светочувствительного материала и полосками оптических модуляторов. Прозрачность каждой полосы, соответствующей оптическому модулятору, может быть изменена электронным способом.

Рис. 9.3. Массив линейных пространственно-световых модуляторов
На рис. 9.4 показана упрощенная конструкция из линейных модуляторов, используемая в качестве оптического умножителя матриц. Горизонтальные полосы оптических модуляторов управляются электронным способом. Светопроводность каждой полосы соответствует величине соответствующей компоненты входного вектора X, тем самым определяя величину светового потока через соответствующую строку весовой матрицы. В этой системе нет отдельных световых потоков для каждой световой строки; один источник света через коллиматор создает световой поток, входящий справа и проходящий через каждую полосу модулятора на весовую маску. Свет, проходящий через эту маску, попадает на вертикальные светочувствительные столбцы. Каждый столбец производит выход, пропорциональный суммарному световому потоку, проходящему через соответствующий столбец весовой маски.
Таким образом, результат аналогичен описанному ранее для линзовой системы, концентрирующей свет на маленьком фотодетекторе; данная система производит умножение матриц с точно таким же результатом.

Рис. 9.4. Линейный модулятор, используемый в качестве
оптического матричного умножителя.
Так как массивы линейных модуляторов передают свет, прошедший коллиматор, для данной системы не требуется цилиндрических линз. Это решает трудную проблему геометрических искажений, связанную с использовавшейся ранее оптикой. Преимущества компактной конструкции и оптической простоты, в то же время, приводят к относительно низкой скорости функционирования; современные технологии требуют десятков микросекунд для переключения световых модуляторов.
Реализация ДАП с использованием массивов линейных модуляторов. На рис. 9.5 приведена структура ДАП, сконструированной с использованием массивов линейных модуляторов. Она аналогична структуре описанного выше умножителя, за исключением того, что каждая полоса столбца светового детектора слева управляет пороговыми цепями, которые в свою очередь управляют светопроводностью связанной с ними вертикальной полосы. Таким образом, модулируется второй световой источник слева и соответствующий столбец весовой маски получает управлямый уровень освещенности. Это вырабатывает необходимый сигнал обратной связи для горизонтальных строк световых детекторов справа; их выходные сигналы обрабатываются пороговой функцией и управляют светопроводностью соответствующих горизонтальных светомодулирующих полос, тем самым замыкая петлю обратной связи ДАП.

Рис. 9.5. Оптическая двунаправленная ассоциативная память,
использующая массивы линейных модуляторов.
Сети с обратными связями
У сетей, рассмотренных до сих пор, не было обратных связей, т.е. соединений, идущих от выходов некоторого слоя к входам этого же слоя или предшествующих слоев. Этот специальный класс сетей, называемых сетями без обратных связей или сетями прямого распространения, представляет интерес и широко используется. Сети более общего вида, имеющие соединения от выходов к входам, называются сетями с обратными связями. У сетей без обратных связей нет памяти, их выход полностью определяется текущими входами и значениями весов. В некоторых конфигурациях сетей с обратными связями предыдущие значения выходов возвращаются на входы; выход, следовательно, определяется как текущим входом, так и предыдущими выходами. По этой причине сети с обратными связями могут обладать свойствами, сходными с кратковременной человеческой памятью, сетевые выходы частично зависят от предыдущих входов.
Скорость
Способность сети быстро производить вычисления является ее главным достоинством. Она обусловлена высокой степенью распараллеливания вычислительного процесса. Если сеть реализована на аналоговой электронике, то решение редко занимает промежуток времени, больший нескольких постоянных времени сети. Более того, время сходимости слабо зависит от размерности задачи. Это резко контрастирует с более чем экспоненциальным ростом времени решения при использовании обычных подходов. Моделирование с помощью однопроцессорных систем не позволяет использовать преимущества параллельной архитектуры, но современные мультипроцессорные системы типа Connection Machine (65536 процессоров!) весьма многообещающи для решения трудных задач.
Слои Кохоненна
В своей простейшей форме слой Кохонена функционирует в духе «победитель забирает все», т.е. для данного входного вектора один и только один нейрон Кохонена выдает на выходе логическую единицу, все остальные выдают ноль. Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них.
Ассоциированное с каждым нейроном Кохонена множество весов соединяет его с каждым входом. Например, на рис. 4.1 нейрон Кохонена К1
имеет веса w11, w21, …, wm1, составляющие весовой вектор W1. Они соединяются-через входной слой с входными сигналами х1, x2, …, xm, составляющими входной вектор X. Подобно нейронам большинства сетей выход NET каждого нейрона Кохонена является просто суммой взвешенных входов. Это может быть выражено следующим образом:
NETj
= w1jx1 + w2jx2
+ … + wmjxm (4.1)
где NETj – это выход NET нейрона Кохонена j,

или в векторной записи
N = XW, (4.3)
где N – вектор выходов NET слоя Кохонена.
Нейрон Кохонена с максимальным значением NET является «победителем». Его выход равен единице, у остальных он равен нулю.
Слой Гроссберга
Слой Гроссберга функционирует в сходной манере. Его выход
NET является взвешенной суммой выходов k1,k2, ..., kn слоя Кохонена, образующих вектор К. Вектор соединяющих весов, обозначенный через V, состоит из весов v11, v21, ..., vnp. Тогда выход NET каждого нейрона Гроссберга есть

где NETj – выход j-го нейрона Гроссберга, или в векторной форме
Y = KV, (4.5)
где Y – выходной вектор слоя Гроссберга, К – выходной вектор слоя Кохонена, V – матрица весов слоя Гроссберга.
Если слой Кохонена функционирует таким образом, что лишь у одного нейрона величина NET равна единице, а у остальных равна нулю, то лишь один элемент вектора К отличен от нуля, и вычисления очень просты. Фактически каждый нейрон слоя Гроссберга лишь выдает величину веса, который связывает этот нейрон с единственным ненулевым нейроном Кохонена.
Соображения надежности
Прежде чем искусственные нейронные сети можно будет использовать там, где поставлены на карту человеческая жизнь или ценное имущество, должны быть решены вопросы, относящиеся к их надежности.
Подобно людям, структуру мозга которых они копируют, искусственные нейронные сети сохраняют в определенной мере непредсказуемость. Единственный способ точно знать выход состоит в испытании всех возможных входных сигналов. В большой сети такая полная проверка практически неосуществима и должны использоваться статистические методы для оценки функционирования. В некоторых случаях это недопустимо. Например, что является допустимым уровнем ошибок для сети, управляющей системой космической обороны? Большинство людей скажет, любая ошибка недопустима, так как ведет к огромному числу жертв и разрушений. Это отношение не меняется от того обстоятельства, что человек в подобной ситуации также может допускать ошибки.
Проблема возникает из-за допущения полной безошибочности компьютеров. Так как искусственные нейронные сети иногда будут совершать ошибки даже при правильном функционировании, то, как ощущается многими, это ведет к ненадежности– качеству, которое мы считаем недопустимым для наших машин.
Сходная трудность заключается в неспособности традиционных искусственных нейронных сетей "объяснить", как они решают задачу. Внутреннее представление, получающееся в результате обучения, часто настолько сложно, что его невозможно проанализировать, за исключением самых простых случаев. Это напоминает нашу неспособность объяснить, как мы узнаем человека, несмотря на различие в расстоянии, угле, освещении и на прошедшие годы. Экспертная система может проследить процесс своих рассуждений в обратном порядке, так что человек может проверить ее на разумность. Сообщалось о встраивании этой способности в искусственные нейронные сети [З], что может существенно повлиять на приемлемость этих систем.
Статистичекие сети Хопфилда
Если правила изменения состояний для бинарной сети Хопфилда заданы статистически, а не детерминированно, как в уравнении (6.1), то возникает система, имитирующая отжиг. Для ее реализации вводится вероятность изменения веса как функция от величины, на которую выход нейрона OUT превышает его порог. Пусть
Ek = NETk – qk,
где NETk – выход NET нейрона k; q – порог нейрона k, и

(отметьте вероятностную функцию Больцмана в знаменателе), где Т – искусственная температура.
В стадии функционирования искусственной температуре Т
приписывается большое значение, нейроны устанавливаются в начальном состоянии, определяемом входным вектором, и сети предоставляется возможность искать минимум энергии в соответствии с нижеследующей процедурой:
1. Приписать состоянию каждого нейрона с вероятностью рk
значение единица, а с вероятностью 1–рk
– нуль.
2. Постепенно уменьшать искусственную температуру и повторять шаг 1, пока не будет достигнуто равновесие.
Статистические свойства обученной сети
Метод обучения Кохонена обладает полезной и интересной способностью извлекать статистические свойства из множества входных данных. Как показано Кохоненом [8], для полностью обученной сети вероятность того, что случайно выбранный входной вектор (в соответствии с функцией плотности вероятности входного множества) будет ближайшим к любому заданному весовому вектору, равна 1/k, где k – число нейронов Кохонена. Это является оптимальным распределением весов на гиперсфере. (Предполагается, что используются все весовые векторы, что имеет место лишь в том случае, если используется один из обсуждавшихся методов распределения весов.)
Структура
Когнитрон конструируется в виде слоев нейронов, соединенных синапсами. Как показано на рис.10.1, предсинаптический нейрон в одном слое связан с постсинаптическим нейроном в следующем слое. Имеются два типа нейронов: возбуждающие узлы, которые стремятся вызвать возбуждение постсинаптического узла, и тормозящие узлы, которые тормозят это возбуждение. Возбуждение нейрона определяется взвешенной суммой его возбуждающих и тормозящих входов, однако в действительности механизм является более сложным, чем простое суммирование.

Рис. 10.1. Пресинаптические и постсинаптические нейроны
На рис. 10.2 показано, что каждый нейрон связан только с нейронами в соседней области, называемой областью связи. Это ограничение области связи согласуется с анатомией зрительной коры, в которой редко соединяются между собой нейроны, располагающиеся друг от друга на расстоянии более одного миллиметра. В рассматриваемой модели нейроны упорядочены в виде слоев со связями от одного слоя к следующему. Это также аналогично послойной структуре зрительной коры и других частей головного мозга.

Рис. 10.2. Область связей нейрона
СТРУКТУРА ДАП

Рис. 7.1. Конфигурация двунаправленной ассоциативной памяти
На рис. 7.1 приведена базовая конфигурация ДАП. Эта конфигурация существенно отличается от используемой в работе [9]. Она выбрана таким образом, чтобы подчеркнуть сходство с сетями Хопфилда и предусмотреть увеличения количества слоев. На рис. 7.1 входной вектор А
обрабатывается матрицей весов W сети, в результате чего вырабатывается вектор выходных сигналов нейронов В. Вектор В затем обрабатывается транспонированной матрицей Wt весов сети, которая вырабатывает новые выходные сигналы, представляющие собой новый входной вектор А. Этот процесс повторяется до тех пор, пока сеть не достигнет стабильного состояния, в котором ни вектор А, ни вектор В не изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней значение функции активации F. Этот процесс может быть выражен следующим образом:

или в векторной форме:
В = F(AW), (7.2)
где В – вектор выходных сигналов нейронов слоя 2, А – вектор выходных сигналов нейронов слоя 1, W – матрица весов связей между слоями 1 и 2, F
– функция активации.
Аналогично
A = F(BWt) (7.3)
где
Wt является транспозицией матрицы W.
Как отмечено в гл. 1, Гроссберг показал преимущества использования сигмоидальной (логистической) функции активации

где OUTi – выход нейрона i, NETi – взвешенная сумма входных сигналов нейрона i, l – константа, определяющая степень кривизны.
В простейших версиях ДАП значение константы l выбирается большим, в результате чего функция активации приближается к простой пороговой функции. В дальнейших рассуждениях будем предполагать, что используется пороговая функция активации.
Примем также, что существует память внутри каждого нейрона в слоях 1 и 2 и что выходные сигналы нейронов изменяются одновременно с каждым тактом синхронизации, оставаясь постоянными между этими тактами. Таким образом, поведение нейронов может быть описано следующими правилами:
OUTi(n+1)
= 1, если NETi(n)>0,
OUTi(n+l) = 0, если NETi(n)<0,
OUTi(n+l) = OUT(n), если NETi(n) = 0,
где OUTi(n) представляет собой величину выходного сигнала нейрона i в момент времени п.
Заметим, что как и в описанных ранее сетях слой 0 не производит вычислений и не имеет памяти; он является только средством распределения выходных сигналов слоя 2 к элементам матрицы Wt.
СТРУКТУРА СЕТИ
На рис.4.1 показана упрощенная версия прямого действия сети встречного распространения. На нем иллюстрируются функциональные свойства этой парадигмы. Полная двунаправленная сеть основана на тех же принципах, она обсуждается в этой главе позднее.

Рис. 4.1. Сеть с встречным распознаванием без обратных связей
Нейроны слоя 0 (показанные кружками) служат лишь точками разветвления и не выполняют вычислений. Каждый нейрон слоя 0 соединен с каждым нейроном слоя 1 (называемого слоем Кохонена) отдельным весом wmn.
Эти веса в целом рассматриваются как матрица весов W. Аналогично, каждый нейрон в слое Кохонена (слое 1) соединен с каждым нейроном в слое Гроссберга (слое 2) весом vnp. Эти веса образуют матрицу весов V. Все это весьма напоминает другие сети, встречавшиеся в предыдущих главах, различие, однако, состоит в операциях, выполняемых нейронами Кохонена и Гроссберга.
Как и многие другие сети, встречное распространение функционирует в двух режимах: в нормальном режиме, при котором принимается входной вектор Х и выдается выходной вектор Y, и в режиме обучения, при котором подается входной вектор и веса корректируются, чтобы дать требуемый выходной вектор.
СВОЙСТВА ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
Искусственные нейронные сети индуцированы биологией, так как они состоят из элементов, функциональные возможности которых аналогичны большинству элементарных функций биологического нейрона. Эти элементы затем организуются по способу, который может соответствовать (или не соответствовать) анатомии мозга. Несмотря на такое поверхностное сходство, искусственные нейронные сети демонстрируют удивительное число свойств присущих мозгу. Например, они обучаются на основе опыта, обобщают предыдущие прецеденты на новые случаи и извлекают существенные свойства из поступающей информации, содержащей излишние данные.
Несмотря на такое функциональное сходство, даже самый оптимистичный их защитник не предположит, что в скором будущем искусственные нейронные сети будут дублировать функции человеческого мозга. Реальный «интеллект», демонстрируемый самыми сложными нейронными сетями, находится ниже уровня дождевого червя, и энтузиазм должен быть умерен в соответствии с современными реалиями. Однако равным образом было бы неверным игнорировать удивительное сходство в функционировании некоторых нейронных сетей с человеческим мозгом. Эти возможности, как бы они ни были ограничены сегодня, наводят на мысль, что глубокое проникновение в человеческий интеллект, а также множество революционных приложений, могут быть не за горами.
Теоремы APT
В работе [2] доказаны некоторые теоремы, показывающие характеристики сетей APT. Четыре результата, приведенные ниже, являются одними из наиболее важных:
1. После стабилизации процесса обучения предъявление одного из обучающих векторов (или вектора с существенными характеристиками категории) будет активизировать требуемый нейрон слоя распознавания без поиска. Эта характеристика «прямого доступа» определяет быстрый доступ к предварительно изученным образам.
2. Процесс поиска является устойчивым. После определения выигравшего нейрона в сети не будет возбуждений других нейронов в результате изменения векторов выхода слоя сравнения С; только сигнал сброса может вызвать такие изменения.
3. Процесс обучения является устойчивым. Обучение не будет вызывать переключения с одного возбужденного нейрона слоя распознавания на другой.
4. Процесс обучения конечен. Любая последовательность произвольных входных векторов будет производить стабильный набор весов после конечного количества обучающих серий; повторяющиеся последовательности обучающих векторов не будут приводить к циклическому изменению весов.
Терминология
Многие авторы избегают термина «нейрон» для обозначения искусственного нейрона, считая его слишком грубой моделью своего биологического прототипа. В этой книге термины «нейрон», «клетка», «элемент» используются взаимозаменяемо для обозначения «искусственного нейрона» как краткие и саморазъясняющие.
ТЕРМИНОЛОГИЯ, ОБОЗНАЧЕНИЯ И СХЕМАТИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
К сожалению, для искусственных нейронных сетей еще нет опубликованных стандартов и устоявшихся терминов, обозначений и графических представлений. Порой идентичные сетевые парадигмы, представленные различными авторами, покажутся далекими друг от друга. В этой книге выбраны наиболее широко используемые термины.
Термодинамические системы
Металл отжигают, нагревая его до температуры, превышающей точку его плавления, а затем давая ему медленно остыть. При высоких температурах атомы, обладая высокими энергиями и свободой перемещения, случайным образом принимают все возможные конфигурации. При постепенном снижении температуры энергии атомов уменьшаются, и система в целом стремится принять конфигурацию с минимальной энергией. Когда охлаждение завершено, достигается состояние глобального минимума энергии.
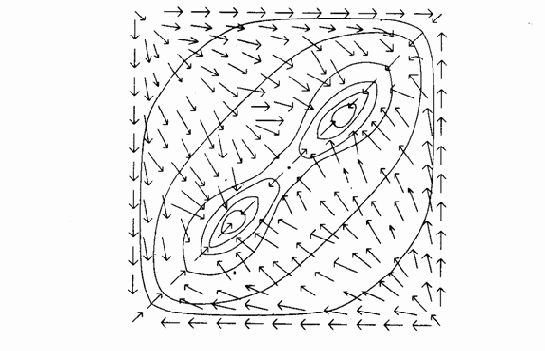
Рис.6.3. Линии энергетических уровнен
При фиксированной температуре распределение энергий системы определяется вероятностным фактором Больцмана
exp(–E/kT),
где Е – энергия системы; k – постоянная Больцмана; Т – температура.
Отсюда можно видеть, что имеется конечная вероятность того, что система обладает высокой энергией даже при низких температурах. Сходным образом имеется небольшая, но вычисляемая вероятность, что чайник с водой на огне замерзнет, прежде чем закипеть.
Статистическое распределение энергий позволяет системе выходить из локальных минимумов энергии. В то же время вероятность высокоэнергетических состояний быстро уменьшается со снижением температуры. Следовательно, при низких температурах имеется сильная тенденция занять низкоэнергетическое состояние.
Трудности с алгоритмом обучения Коши
Несмотря на улучшение скорости обучения, даваемое машиной Коши по сравнению с машиной Больцмана, время сходимости все еще может в 100 раз превышать время для алгоритма обратного распространения. Отметим, что сетевой паралич особенно опасен для алгоритма обучения Коши, в особенности для сети с нелинейностью типа логистической функции. Бесконечная дисперсия распределения Коши приводит к изменениям весов неограниченной величины. Далее, большие изменения весов будут иногда приниматься даже в тех случаях, когда они неблагоприятны, часто приводя к сильному насыщению сетевых нейронов с вытекающим отсюда риском паралича.
Трудности с алгоритмом обучения персептрона
Может оказаться затруднительным определить, выполнено ли условие разделимости для конкретного обучающего множества. Кроме того, во многих встречающихся на практике ситуациях входы часто меняются во времени и могут быть разделимы в один момент времени и неразделимы в другой. В доказательстве алгоритма обучения персептрона ничего не говорится также о том, сколько шагов требуется для обучения сети. Мало утешительного в знании того, что обучение закончится за конечное число шагов, если необходимое для этого время сравнимо с геологической эпохой. Кроме того, не доказано, что персептронный алгоритм обучения более быстр по сравнению с простым перебором всех возможных значений весов, и в некоторых случаях этот примитивный подход может оказаться лучше.
На эти вопросы никогда не находилось удовлетворительного ответа, они относятся к природе обучающего материала. В различной форме они возникают в последующих главах, где рассматриваются другие сетевые парадигмы. Ответы для современных сетей как правило не более удовлетворительны, чем для персептрона. Эти проблемы являются важной областью современных исследований.
Трудности, связанные с обратным распространением
Несмотря на мощь, продемонстрированную методом обратного распространения, при его применении возникает ряд трудностей, часть из которых, однако, облегчается благодаря использованию нового алгоритма.
Сходимость. В работе [5] доказательство сходимости дается на языке дифференциальных уравнений в частных производных, что делает его справедливым лишь в том случае, когда коррекция весов выполняется с помощью бесконечно малых шагов. Так как это ведет к бесконечному времени сходимости, то оно теряет силу в практических применениях. В действительности нет доказательства, что обратное распространение будет сходиться при конечном размере шага. Эксперименты показывают, что сети обычно обучаются, но время обучения велико и непредсказуемо.
Локальные минимумы. В обратном распространении для коррекции весов сети используется градиентный спуск, продвигающийся к минимуму в соответствии с локальным наклоном поверхности ошибки. Он хорошо работает в случае сильно изрезанных невыпуклых поверхностей, которые встречаются в практических задачах. В одних случаях локальный минимум является приемлемым решением, в других случаях он неприемлем.
Даже после того как сеть обучена, невозможно сказать, найден ли с помощью обратного распространения глобальный минимум. Если решение неудовлетворительно, приходится давать весам новые начальные случайные значения и повторно обучать сеть без гарантии, что обучение закончится на этой попытке или что глобальный минимум вообще будет когда либо найден.
Паралич. При некоторых условиях сеть может при обучении попасть в такое состояние, когда модификация весов не ведет к действительным изменениям сети. Такой «паралич сети» является серьезной проблемой: один раз возникнув, он может увеличить время обучения на несколько порядков.
Паралич возникает, когда значительная часть нейронов получает веса, достаточно большие, чтобы дать большие значения NET. Это приводит к тому, что величина OUT приближается к своему предельному значению, а производная от сжимающей функции приближается к нулю. Как мы видели, алгоритм обратного распространения при вычислении величины изменения веса использует эту производную в формуле в качестве коэффициента. Для пораженных параличом нейронов близость производной к нулю приводит к тому, что изменение веса становится близким к нулю.
Если подобные условия возникают во многих нейронах сети, то обучение может замедлиться до почти полной остановки.
Нет теории, способной предсказывать, будет ли сеть парализована во время обучения или нет. Экспериментально установлено, что малые размеры шага реже приводят к параличу, но шаг, малый для одной задачи, может оказаться большим для другой. Цена же паралича может быть высокой. При моделировании многие часы машинного времени могут уйти на то, чтобы выйти из паралича.
Упрощенная архитектура APT
На рис.8.1 показана упрощенная конфигурация сети APT, представленная в виде пяти функциональных модулей. Она включает два слоя нейронов, так называемых «слой сравнения» и «слой распознавания». Приемник 1, Приемник 2 и Сброс обеспечивают управляющие функции, необходимые для обучения и классификации.
Перед рассмотрением вопросов функционирования сети в целом необходимо рассмотреть отдельно функции модулей; далее обсуждаются функции каждого из них.
Слой сравнения. Слой сравнения получает двоичный входной вектор Х и первоначально пропускает его неизмененным для формирования выходного вектора C. На более поздней фазе в распознающем слое вырабатывается двоичный вектор R, модифицирующий вектор C, как описано ниже.
Каждый нейрон в слое сравнения (рис. 8.2) получает три двоичных входа (0 или I): (1) компонента хi входного вектора X; (2) сигнал обратной связи Ri – взвешенная сумма выходов распознающего слоя; (3) вход от Приемника 1 (один и тот же сигнал подается на все нейроны этого слоя).

Рис. 8.1. Упрощенная сеть АРТ

Рис. 8.2. Упрощенный слон сравнения
Чтобы получить на выходе нейрона единичное значение, как минимум два из трех его входов должны равняться единице; в противном случае его выход будет нулевым. Таким образом реализуется правило двух третей, описанное в [З]. Первоначально выходной сигнал G1 Приемника 1 установлен в единицу, обеспечивая один из необходимых для возбуждения нейронов входов, а все компоненты вектора R установлены в 0; следовательно, в этот момент вектор C
идентичен двоичному входному вектору X.
Слой распознавания. Слой распознавания осуществляет классификацию входных векторов. Каждый нейрон в слое распознавания имеет соответствующий вектор весов Bj Только один нейрон с весовым вектором, наиболее соответствующим входному вектору, возбуждается; все остальные нейроны заторможены.
Как показано на рис. 8.3, нейрон в распознающем •слое имеет, максимальную реакцию, если вектор C, являющийся выходом слоя сравнения, соответствует набору его весов, следовательно, веса представляют запомненный образ или экземпляр для категории входных векторов.
Эти веса являются действительными числами, а не двоичными величинами. Двоичная версия этого образа также запоминается в соответствующем наборе весов слоя сравнения (рис. 8.2); этот набор состоит из весов связей, соединяющих определенные нейроны слоя распознавания, один вес на каждый нейрон слоя сравнения.
В процессе функционирования каждый нейрон слоя распознавания вычисляет свертку вектора собственных весов и входного вектора C. Нейрон, имеющий веса, наиболее близкие вектору C, будет иметь самый большой выход, тем самым выигрывая соревнование и одновременно затормаживая все остальные нейроны в слое.
Как показано на рис. 8.4, нейроны внутри слоя распознавания взаимно соединены в латерально-тормозящую сеть. В простейшем случае (единственном, рассмотренном в данной работе) предусматривается, что только один нейрон в слое возбуждается в каждый момент времени (т. е. только нейрон с наивысшим уровнем активации будет иметь единичный выход; все остальные нейроны будут иметь нулевой выход). Эта конкуренция реализуется введением связей с отрицательными весами lij с выхода каждого нейрона ri на входы остальных нейронов. Таким образом, если нейрон имеет большой выход, он тормозит все остальные нейроны в слое. Кроме того, каждый нейрон имеет связь с положительным весом со своего выхода на свой собственный вход. Если нейрон имеет единичный выходной уровень, эта обратная связь стремится усилить и поддержать его.

Рис. 8.3. Упрощенный слой распознавания
Приемник 2. G2, выход Приемника 2, равен единице, если входной вектор X имеет хотя бы одну единичную компоненту. Более точно, G2 является логическим ИЛИ от компонента вектора X.
Приемник 1. Как и сигнал G2, выходной сигнал G1 Приемника 1 равен 1, если хотя бы одна компонента двоичного входного вектора X равна единице; однако если хотя бы одна компонента вектора R равна единице, G1 устанавливается в нуль. Таблица, определяющая эти соотношения:

Рис. 8.4. Слой распознавания с латеральным торможением
|
ИЛИ от компонента вектора X |
ИЛИ от компонента вектора R |
G1 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
0 |
1 |
0 |
В процессе функционирования модуль сброса вычисляет сходство как отношение количества единиц в векторе C к их количеству в векторе C. Если это отношение ниже значения параметра сходства, вырабатывается сигнал сброса.
Устойчивость
Как и в других сетях, веса между слоями в этой сети могут рассматриваться в виде матрицы
W. В работе [2] показано, что сеть с обратными связями является устойчивой, если ее матрица симметрична и имеет нули на главной диагонали, т.е. если wij = wji
и wii = 0 для всех i.
Устойчивость такой сети может быть доказана с помощью элегантного математического метода. Допустим, что найдена функция, которая всегда убывает при изменении состояния сети. В конце концов эта функция должна достичь минимума и прекратить изменение, гарантируя тем самым устойчивость сети. Такая функция, называемая функцией Ляпунова, для рассматриваемых сетей с обратными связями может быть введена следующим образом:

где Е – искусственная энергия сети;
wij – вес от выхода нейрона i к входу нейрона j; OUTj – выход нейрона j; Ij – внешний вход нейрона j; Тj
– порог нейрона j.
Изменение энергии Е, вызванное изменением состояния j-нейрона, есть

где ?OUTj – изменение выхода j-го нейрона.
Допустим, что величина NET нейрона j
больше порога. Тогда выражение в скобках будет положительным, а из Уравнения (6.1) следует, что выход нейрона j должен измениться в положительную сторону (или остаться без изменения). Это значит, что ?OUT. может быть только положительным или нулем и ?Е должно быть отрицательным. Следовательно, энергия сети должна либо уменьшиться, либо остаться без изменения.
Далее, допустим, что величина NET меньше порога. Тогда величина ?OUTj может быть только отрицательной или нулем. Следовательно, опять энергия должна уменьшиться или остаться без изменения.
И окончательно, если величина NET равна порогу, ?j равна нулю и энергия остается без изменения.
Это показывает, что любое изменение состояния нейрона либо уменьшит энергию, либо оставит ее без изменения. Благодаря такому непрерывному стремлению к уменьшению энергия в конце концов должна достигнуть минимума и прекратить изменение. По определению такая сеть является устойчивой.
Симметрия сети является достаточным, но не необходимым условием для устойчивости системы. Имеется много устойчивых систем (например, все сети прямого действия!), которые ему не удовлетворяют. Можно продемонстрировать примеры, в которых незначительное отклонение от симметрии может приводить к непрерывным осцилляциям. Однако приближенной симметрии обычно достаточно для устойчивости систем.
ВЕКТОРНО-МАТРИЧНЫЕ УМНОЖИТЕЛИ
Процесс функционирования большинства искусственных нейронных сетей может быть описан математически в виде последовательных умножений вектора на матрицу, одна операция умножения в каждом слое. Для вычисления выхода слоя входной вектор умножается на матрицу весовых коэффициентов, образуя вектор NET. К этому вектору прикладывается затем функция активации F, образуя вектор OUT, являющийся выходом слоя.
Символически
NET = XW,
OUT = F(NET),
где NET – вектор в виде строки, сформированный взвешенными суммами входов; OUT – выходной вектор; Х – входной вектор; W – матрица весовых коэффициентов.
В биологических нейронных сетях эта операций выполняется большим количеством работающих одновременно нейронов, поэтому система работает быстро, несмотря на медленную работу отдельных нейронов.
Когда искусственные нейронные сети моделируются на универсальных компьютерах, присущая им параллельная природа вычислений теряется; каждая операция должна быть выполнена последовательно. Несмотря на большую скорость выполнения отдельных вычислений, количество операций, необходимых для выполнения умножения матриц, пропорционально квадрату размерности входного вектора (если входной и выходной векторы имеют одинаковую размерность), и время вычислений может стать слишком большим.
ВХОДНЫЕ И ВЫХОДНЫЕ ЗВЕЗДЫ
Много общих идей, используемых в искусственных нейронных сетях, прослеживаются в работах Гроссберга; в качестве примера можно указать конфигурации входных и выходных звезд [I], используемые во многих сетевых парадигмах. Входная звезда, как показано на рис.Б.1, состоит из нейрона, на который подается группа входов через синапсические веса. Выходная звезда, показанная на рис. Б.2, является нейроном, управляющим группой весов. Входные и выходные звезды могут быть взаимно соединены в сети любой сложности; Гроссберг рассматривает их как модель определенных биологических функций. Вид звезды определяет ее название, однако звезды обычно изображаются в сети иначе.

Рис. Б.2. Сеть «Аутстар» Гроссберга
ВОССТАНОВЛЕНИЕ ЗАПОМНЕННЫХ АССОЦИАЦИЙ
Долговременная память (или ассоциации) реализуется в весовых массивах W и Wt. Каждый образ состоит из двух векторов: вектора A, являющегося выходом слоя1, и вектора B, ассоциированного образа, являющегося выходом слоя 2. Для восстановления ассоциированного образа вектор A или его часть кратковременно устанавливаются на выходах слоя 1. Затем вектор A удаляется и сеть приводится в стабильное состояние, вырабатывая ассоциированный вектор B на выходе слоя 2. Затем вектор B
воздействует через транспонированную матрицу Wt, воспроизводя воздействие исходного входного вектора A на выходе слоя 1. Каждый такой цикл вызывает уточнение выходных векторов слоя 1 и 2 до тех пор, пока не будет достигнута точка стабильности в сети. Эта точка может быть рассмотрена как резонансная, так как вектор передается обратно и вперед между слоями сети, всегда обрабатывая текущие выходные сигналы, но больше не изменяя их. Состояние нейронов представляет собой кратковременную память (КП), так как оно может быстро изменяться при появлении другого входного вектора. Значения коэффициентов весовой матрицы образуют долговременную память и могут изменяться только на более длительном отрезке времени, используя представленные ниже в данном разделе методы.
В работе [9] показано, что сеть функционирует в направлении минимизации функции энергии Ляпунова в основном таким же образом, как и сети Хопфилда в процессе сходимости (см. гл. 6). Таким образом, каждый цикл модифицирует систему в направлении энергетического минимума, расположение которого определяется значениями весов.

Рис. 7.2. Энергетическая поверхность двунаправленной ассоциативной памяти
Этот процесс может быть визуально представлен в форме направленного движения мяча по резиновой ленте, вытянутой над столом, причем каждому запомненному образу соответствует точка, «вдавленная» в направлении поверхности стола. Рис. 7.2 иллюстрирует данную аналогию с одним запомненным образом. Данный процесс формирует минимум гравитационной энергии в каждой точке, соответствующей запомненному образу, с соответствующим искривлением поля притяжения в направлении к данной точке. Свободно движущийся мяч попадает в поле притяжения и в результате будет двигаться в направлении энергетического минимума, где и остановится.
Временная неустойчивость
Если сеть учится распознавать буквы, то нет смысла учить «Б», если при этом забывается «А». Процесс обучения должен быть таким, чтобы сеть обучалась на всем обучающем множестве без пропусков того, что уже выучено. В доказательстве сходимости [7] это условие выполнено, но требуется также, чтобы сети предъявлялись все векторы обучающего множества прежде, чем выполняется коррекция весов. Необходимые изменения весов должны вычисляться на всем множестве, а это требует дополнительной памяти; после ряда таких обучающих циклов веса сойдутся к минимальной ошибке. Этот метод может оказаться бесполезным, если сеть находится в постоянно меняющейся внешней среде, так что второй раз один и тот же вектор может уже не повториться. В этом случае процесс обучения может никогда не сойтись, бесцельно блуждая или сильно осциллируя. В этом смысле обратное распространение не похоже на биологические системы. Как будет указано в гл.8, это несоответствие (среди прочих) привело к системе ART, принадлежащей Гроссбергу.
ВВЕДЕНИЕ В ПРОЦЕДУРУ ОБРАТНОГО РАСПРОСТРАНЕНИЯ
Долгое время не было теоретически обоснованного алгоритма для обучения многослойных искусственных нейронных сетей. А так как возможности представления с помощью однослойных нейронных сетей оказались весьма ограниченными, то и вся область в целом пришла в упадок.
Разработка алгоритма обратного распространения сыграла важную роль в возрождении интереса к искусственным нейронным сетям. Обратное распространение– это систематический метод для обучения многослойных искусственных нейронных сетей. Он имеет солидное математическое обоснование. Несмотря на некоторые ограничения, процедура обратного распространения сильно расширила область проблем, в которых могут быть использованы искусственные нейронные сети, и убедительно продемонстрировала свою мощь.
Интересна история разработки процедуры. В [7] было дано ясное и полное описание процедуры. Но как только эта работа была опубликована, оказалось, что она была предвосхищена в [4]. А вскоре выяснилось, что еще раньше метод был описан в [12]. Авторы работы [7] сэкономили бы свои усилия, знай они о работе [12]. Хотя подобное дублирование является обычным явлением для каждой научной области, в искусственных нейронных сетях положение с этим намного серьезнее из-за пограничного характера самого предмета исследования. Исследования по нейронным сетям публикуются в столь различных книгах и журналах, что даже самому квалифицированному исследователю требуются значительные усилия, чтобы быть осведомленным о всех важных работах в этой области.
ВВЕДЕНИЕ В СЕТИ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ
Возможности сети встречного распространения, разработанной в [5-7], превосходят возможности однослойных сетей. Время же обучения по сравнению с обратным распространением может уменьшаться в сто раз. Встречное распространение не столь общо, как обратное распространение, но оно может давать решение в тех приложениях, где долгая обучающая процедура невозможна. Будет показано, что помимо преодоления ограничений других сетей встречное распространение обладает собственными интересными и полезными свойствами.
Во встречном распространении объединены два хорошо известных алгоритма: самоорганизующаяся карта Кохонена [8] и звезда Гроссберга [2-4] (см. приложение Б). Их объединение ведет к свойствам, которых нет ни у одного из них в отдельности.
Методы, которые подобно встречному распространению, объединяют различные сетевые парадигмы как строительные блоки, могут привести к сетям, более близким к мозгу по архитектуре, чем любые другие однородные структуры. Похоже, что в мозгу именно каскадные соединения модулей различной специализации позволяют выполнять требуемые вычисления.
Сеть встречного распространения функционирует подобно столу справок, способному к обобщению. В процессе обучения входные векторы ассоциируются с соответствующими выходными векторами. Эти векторы могут быть двоичными, состоящими из нулей и единиц, или непрерывными. Когда сеть обучена, приложение входного вектора приводит к требуемому выходному вектору. Обобщающая способность сети позволяет получать правильный выход даже при приложении входного вектора, который является неполным или слегка неверным. Это позволяет использовать данную сеть для распознавания образов, восстановления образов и усиления сигналов.
Выбор начальных значений весовых векторов
Всем весам сети перед началом обучения следует придать начальные значения. Общепринятой практикой при работе с нейронными сетями является присваивание весам небольших случайных значений. При обучении слоя Кохонена случайно выбранные весовые векторы следует нормализовать. Окончательные значения весовых векторов после обучения совпадают с нормализованными входными векторами. Поэтому нормализация перед началом обучения приближает весовые векторы к их окончательным значениям, сокращая, таким образом, обучающий процесс.
Рандомизация весов слоя Кохонена может породить серьезные проблемы при обучении, так как в результате ее весовые векторы распределяются равномерно по поверхности гиперсферы. Из-за того, что входные векторы, как правило, распределены неравномерно и имеют тенденцию группироваться на относительно малой части поверхности гиперсферы, большинство весовых векторов будут так удалены от любого входного вектора, что они никогда не будут давать наилучшего соответствия. Эти нейроны Кохонена будут всегда иметь нулевой выход и окажутся бесполезными. Более того, оставшихся весов, дающих наилучшие соответствия, может оказаться слишком мало, чтобы разделить входные векторы на классы, которые расположены близко друг к другу на поверхности гиперсферы.
Допустим, что имеется несколько множеств входных векторов, все множества сходные, но должны быть разделены на различные классы. Сеть должна быть обучена активировать отдельный нейрон Кохонена для каждого класса. Если начальная плотность весовых векторов в окрестности обучающих векторов слишком мала, то может оказаться невозможным разделить сходные классы из-за того, что не будет достаточного количества весовых векторов в интересующей нас окрестности, чтобы приписать по одному из них каждому классу входных векторов.
Наоборот, если несколько входных векторов получены незначительными изменениями из одного и того же образца и должны быть объединены в один класс, то они должны включать один и тот же нейрон Кохонена. Если же плотность весовых векторов очень высока вблизи группы слегка различных входных векторов, то каждый входной вектор может активировать отдельный нейрон Кохонена.
Это не является катастрофой, так как слой Гроссберга может отобразить различные нейроны Кохонена в один и тот же выход, но это расточительная трата нейронов Кохонена.
Наиболее желательное решение состоит в том, чтобы распределять весовые векторы в соответствии с плотностью входных векторов, которые должны быть разделены, помещая тем самым больше весовых векторов в окрестности большого числа входных векторов. На практике это невыполнимо, однако существует несколько методов приближенного достижения тех же целей.
Одно из решений, известное под названием метода выпуклой комбинации (convex combination method), состоит в том, что все веса приравниваются одной и той же величине

где п – число входов и, следовательно, число компонент каждого весового вектора. Благодаря этому все весовые векторы совпадают и имеют единичную длину. Каждой же компоненте входа Х придается значение

где п – число входов. В начале a очень мало, вследствие чего все входные векторы имеют длину, близкую к

постепенно возрастает, приближаясь к единице. Это позволяет разделять входные векторы и окончательно приписывает им их истинные значения. Весовые векторы отслеживают один или небольшую группу входных векторов и в конце обучения дают требуемую картину выходов. Метод выпуклой комбинации хорошо работает, но замедляет процесс обучения, так как весовые векторы подстраиваются к изменяющейся цели. Другой подход состоит в добавлении шума к входным векторам. Тем самым они подвергаются случайным изменениям, схватывая в конце концов весовой вектор. Этот метод также работоспособен, но еще более медленен, чем метод выпуклой комбинации.
Третий метод начинает со случайных весов, но на начальной стадии обучающего процесса подстраивает все веса, а не только связанные с выигравшим нейроном Кохонена. Тем самым весовые векторы перемещаются ближе к области входных векторов.В процессе обучения коррекция весов начинает производиться лишь для ближайших к победителю нейронов Кохонена. Этот радиус коррекции постепенно уменьшается, так что в конце концов корректируются только веса, связанные с выигравшим нейроном Кохонена.
Еще один метод наделяет каждый нейрон Кохонена «Чувством справедливости». Если он становится победителем чаще своей законной доли времени (примерно 1/k, где k – число нейронов Кохонена), он временно увеличивает свой порог, что уменьшает его шансы на выигрыш, давая тем самым возможность обучаться и другим нейронам.
Во многих приложениях точность результата существенно зависит от распределения весов. К сожалению, эффективность различных решений исчерпывающим образом не оценена и остается проблемой.
Вычисления
Простые узлы в неокогнитроне имеют точно такие же характеристики, что и описанные для когнитрона, и используют те же формулы для определения их выхода. Здесь они не повторяются.
Тормозящий узел вырабатывает выход, пропорциональный квадратному корню из взвешенной суммы квадратов его входов. Заметим, что входы в тормозящий узел идентичны входам соответствующего простого узла и область включает область ответа во всех комплексных плоскостях. В символьном виде

где
v – выход тормозящего узла; i – область над всеми комплексными узлами, с которыми связан тормозящий узел; bi – вес i-й синаптической связи от комплексного узла к тормозящему узлу; ui – выход i-го комплексного узла.
Веса bi
выбираются монотонно уменьшающимися с увеличением расстояния от центра области реакции, при этом сумма их значений должна быть равна единице.
Искусственные нейронные сети являются важным
Искусственные нейронные сети являются важным расширением понятия вычисления. Они обещают создание автоматов, выполняющих функции, бывшие ранее исключительной прерогативой человека. Машины могут выполнять скучные, монотонные и опасные задания, и с развитием технологии возникнут совершенно новые приложения.
Теория искусственных нейронных сетей развивается стремительно, но в настоящее время она недостаточна, чтобы быть опорой для наиболее оптимистических проектов. В ретроспективе видно, что теория развивалась быстрее, чем предсказывали пессимисты, но медленнее, чем надеялись оптимисты, – типичная ситуация. Сегодняшний взрыв интереса привлек к нейронным сетям тысячи исследователей. Резонно ожидать быстрого роста нашего понимания искусственных нейронных сетей, ведущего к более совершенным сетевым парадигмам и множеству прикладных возможностей.
Сети с обратными связями являются перспективным объектом для дальнейших исследований. Их динамическое поведение открывает новые интересные возможности и
ставит специфические проблемы. Как отмечается в гл.9, эти возможности и проблемы сохраняются при реализации нейронных сетей в виде оптических систем.
Задача коммивояжера
Задача коммивояжера является оптимизационной задачей, часто возникающей на практике. Она может быть сформулирована следующим образом: для некоторой группы городов с заданными расстояниями между ними требуется найти кратчайший маршрут с посещением каждого города один раз и с возвращением в исходную точку. Было доказано, что эта задача принадлежит большому множеству задач, называемых «NP-полными» (недетерминистски полиномиальными) [З]. Для NP-полных задач не известно лучшего метода решения, чем полный перебор всех возможных вариантов, и, по мнению большинства математиков, маловероятно, чтобы лучший метод был когда либо найден. Так как такой полный поиск практически неосуществим для большого числа городов, то эвристические методы используются для нахождения приемлемых, хотя и неоптимальных решений.
Описанное в работе [8] решение, основанное на сетях с обратными связями, является типичным в этом отношении. Все же ответ получается так быстро, что в определенных случаях метод может оказаться полезным.
Допустим, что города, которые необходимо посетить, помечены буквами A, B, C и D, а расстояния между парами городов есть dab, dbc и т. д.
Решением является упорядоченное множество из n городов. Задача состоит в отображении его в вычислительную сеть с использованием нейронов в режиме с большой крутизной характеристики (l приближается к бесконечности). Каждый город представлен строкой из n нейронов. Выход одного и только одного нейрона из них равен единице (все остальные равны нулю). Этот равный единице выход нейрона показывает порядковый номер, в котором данный город посещается при обходе. На рис. 6.6 показан случай, когда город C посещается первым, город A – вторым, город D – третьим и город B – четвертым. Для такого представления требуется п2 нейронов – число, которое быстро растет с увеличением числа городов. Длина такого маршрута была бы равна dca
+ dad + ddb + dbc. Так как каждый город посещается только один раз и в каждый момент посещается лишь один город, то в каждой строке и в каждом столбце имеется по одной единице.
Для задачи с п городами всего имеется п! различных маршрутов обхода. Если п = 60, то имеется 6934155х1078 возможных маршрутов. Если принять во внимание, что в нашей галактике (Млечном Пути) имеется лишь 1011 звезд, то станет ясным, что полный перебор всех возможных маршрутов для 1000 городов даже на самом быстром в мире компьютере займет время, сравнимое с геологической эпохой.
Продемонстрируем теперь, как сконструировать сеть для решения этой NP-полной проблемы. Каждый нейрон снабжен двумя индексами, которые соответствуют городу и порядковому номеру его посещения в маршруте. Например, OUTxj = 1 показывает, что город х был j-ым по порядку городом маршрута.
Функция энергии должна удовлетворять двум требованиям: во-первых, должна быть малой только для тех решений, которые имеют по одной единице в каждой строке и в каждом столбце; во-вторых, должна оказывать предпочтение решениям с короткой длиной маршрута.
Первое требование удовлетворяется введением следующей, состоящей из трех сумм, функции энергии:

где A, B и C – некоторые константы. Этим достигается выполнение следующих условий:
1. Первая тройная сумма равна нулю в том и только в том случае, если каждая строка (город) содержит не более одной единицы.
2. Вторая тройная сумма равна нулю в том и только в том случае, если каждый столбец (порядковый номер посещения) содержит не более одной единицы.
3. Третья сумма равна нулю в том и только в том случае, если матрица содержит ровно п
единиц.
|
город |
Порядок следования |
|||
|
1 |
2 |
3 |
4 |
|
|
A |
0 |
1 |
0 |
0 |
|
B |
0 |
0 |
0 |
1 |
|
C |
1 |
0 |
0 |
0 |
|
D |
0 |
0 |
1 |
0 |
Рис. 6.6. Маршрут коммивояжера
Второе требование – предпочтение коротким маршрутам – удовлетворяется с помощью добавления следующего члена к функции энергии:

Заметим, что этот член представляет собой длину любого допустимого маршрута.
Для удобства индексы определяются по модулю n,
т. е. OUTn+j = OUTj, a D – некоторая константа.
При достаточно больших значениях A, B и C низкоэнергетические состояния будут представлять допустимые маршруты, а большие значения D гарантируют, что будет найден короткий маршрут.
Теперь зададим значения весов, т. е. установим соответствие между членами в функции энергии и членами общей формы (см. уравнение 6.2)).
Получаем
wxi,yi = –A?xy(1 – ?ij) (не допускает более одной единицы в строке)
–B?ij(1 – ?xy) (не допускает более одной единицы в столбце)
–С (глобальное ограничение)
–Ddxy(?j,i+1
+ ?j,i-1) (член, отвечающий за длину цикла),
где ?ij = 1, если i = j,
в противном случае ?ij = 0. Кроме того, каждый нейрон имеет смещающий вес хi,
соединенный с +1 и равный Сп.
В работе [8] сообщается об эксперименте, в котором задача коммивояжера была решена для 10 городов. В этом случае возбуждающая функция была равна
OUT = ½ [1 + th(NET/U0)].
Как показали результаты, 16 из 20 прогонов сошлись к допустимому маршруту и около 50% решений оказались кратчайшими маршрутами, как это было установлено с помощью полного перебора. Этот результат станет более впечатляющим, если осознать, что имеется 181440 допустимых маршрутов.
Сообщалось, что сходимость решений, полученных по методу Хопфилда для задачи коммивояжера, в сильной степени зависит от коэффициентов, и не имеется систематического метода определения их значений [11]. В этой работе предложена другая функция энергии с единственным коэффициентом, значение которого легко определяется. В дополнение предложен новый сходящийся алгоритм. Можно ожидать, что новые более совершенные методы будут разрабатываться, так как полностью удовлетворительное решение нашло бы массу применений.
Ограниченная емкость памяти ДАП, ложные
Ограниченная емкость памяти ДАП, ложные ответы и некоторая непредсказуемость поведения привели к рассмотрению ее как устаревшей модели искусственных нейронных сетей.
Этот вывод определенно является преждевременным. ДАП имеет много преимуществ: она совместима с аналоговыми схемами и оптическими системами; для нее быстро сходятся как процесс обучения так, и процесс восстановления информации; она имеет простую и интуитивно привлекательную форму функционирования. В связи с быстрым развитием теории могут быть найдены методы, объясняющие поведение ДАП и разрешающие ее проблемы.
Сети APT являются интересным и важным видом систем. Они способны решить дилемму стабильности-пластичности и хорошо работают с других точек зрения. Архитектура APT сконструирована по принципу биологического подобия; это означает, что ее механизмы во многом соответствуют механизмам мозга (как мы их понимаем). Однако они могут оказаться не в состоянии моделировать распределенную память, которую многие рассматривают как важную характеристику функций мозга. Экземпляры APT представляют собой «бабушкины узелки»; потеря одного узла разрушает всю память. Память мозга, напротив, распределена по веществу мозга, запомненные образы могут часто пережить значительные физические повреждения мозга без полной их потери.
Кажется логичным изучение архитектур, соответствующих нашему пониманию организации и функций мозга. Человеческий мозг представляет существующее доказательство того факта, что решение проблемы распознавания образов возможно. Кажется разумным эмулировать работу мозга, если мы хотим повторить его работу. Однако контраргументом является история полетов; человек не смог оторваться от земли до тех пор, пока не перестал имитировать движения крыльев и полет птиц.
Оптические нейронные сети предлагают огромные выгоды с точки зрения скорости и плотности внутренних связей. Они могут быть использованы (в той или иной форме) для реализации сетей фактически с любой архитектурой.
В настоящее время ограничения электронно-оптических устройств создают множество серьезных проблем, которые должны быть решены прежде, чем оптические нейронные сети получат широкое применение. Однако учитывая, что большое количество превосходных исследователей работает над этой проблемой, а также большую поддержку со стороны военных, можно надеяться на быстрый прогресс в этой области.
Как когнитрон, так и неокогнитрон производят большое впечатление с точки зрения точности, с которой они моделируют биологическую нервную систему. Тот факт, что эти системы показывают результаты, имитирующие некоторые аспекты способностей человека к обучению и познанию, наводит на мысль, что наше понимание функций мозга приближается к уровню, способному принести практическую пользу.
Неокогнитрон является сложной системой и требует существенных вычислительных ресурсов. По этим причинам кажется маловероятным, что такие системы реализуют оптимальное инженерное решение сегодняшних проблем распознавания образов. Однако с 1960 г. стоимость вычислений уменьшалась в два раза каждые два-три года, тенденция, которая, по всей вероятности, сохранится в течение как минимум ближайших десяти лет. Несмотря на то, что многие подходы, казавшиеся нереализуемыми несколько лет назад, являются общепринятыми сегодня и могут оказаться тривиальными через несколько лет, реализация моделей неокогнитрона на универсальных компьютерах является бесперспективной. Необходимо достигнуть тысячекратных улучшений стоимости и производительности компьютеров за счет специализации архитектуры и внедрения технологии СБИС, чтобы сделать неокогнитрон практической системой для решения сложных проблем распознавания образов, однако ни эта, ни какая-либо другая модель искусственных нейронных сетей не должны отвергаться только на основании их высоких вычислительных требований.