Энергетика нейросети
Пытаясь проанализировать, как энергия возбужденого нейрона воздействует на связанные с ним нейроны, мы вновь и вновь приходим к выводу, что она распределяется обратно пропорционально сопротивлениям синапсов «принимающих» нейронов.
Однако наша попытка последовать принципу распределения энергии, кроме существенного усложнения расчетов, привела к следующему.
После частичного обучения нейросети изменение весов для последующего обучения (при демонстрации других эталонов) приводит к перераспределению энергии, к ее оттоку от уже сформировавшихся динамических путей возбуждения. С точки зрения определенного нейрона выходного слоя «рассеянная» энергия устремляется по «чужим» путям возбуждения, и тогда приходится с помощью порогов компенсировать возбуждение нужного пути, поддерживая необходимый уровень энергии.
Здесь лучше всего и проявляется известная традиция построения нейронных сетей, когда возбуждение с выхода нейрона в неизменном виде поступает на каждый вход других нейронов, не распределяясь между ними.
Ориентируясь на программную реализацию нейросети, не станем отступать от традиционных принципов, используя не «физический» подход, а информационный.
Для того чтобы сделать конкретный вывод, рассчитаем вариант той же «готовой» сети (см. рис. 2.12) с распределением энергии, увеличив веса связей, которые не приняли участие в трассировке, т.е. веса, первоначально не равные нулю. Положим их равными 0,5.
Рассмотрим эталон {A1,B2,C3}, требующий решения R2. Покажем, как рассчитывать сеть, предоставив возможность читателю установить правильность ее работы:

Формализация нейросети
Тактирование работы сети, столь характерное для каждой управляющей системы, отслеживающей ее состояние в дискретные моменты времени, определяет потактовое продвижение по ней волны возбуждений от входного слоя к выходному. Волна за волной возбуждения имитируют систолическую схему вычислений
— параллельный конвейер обработки отдельных кадров, соответствующих конфигурации возбуждений входного слоя в одном такте.
На практике широко исследуются многослойные сети типа персептрон, где отсутствуют обратные связи и возможны связи между нейронами только смежных слоев. В данном разделе мы также не рассматриваем обратные связи, но снимаем ограничение на «слоистость» нейросети, что обеспечивает более общий подход. Именно такая нейросеть, допускающая связи «через слой», была построена в приведенном выше примере. Для таких сетей значительно упрощаются следующие построения.
Нейронную сеть можно изучать статически, исследуя ее структуру, и динамически, анализируя прохождение возбуждений.
Статические исследования нейросети показывают, что она представляет собой ориентированный граф G без контуров. Вершины его соответствуют нейронам, дуги — синапсическим связям. Целесообразно такой, высший, уровень представления отделить от более глубокого описания каждого нейрона и связей между ними, отображающего динамику проходящих процессов, т.е. расчет значения возбуждения нейронов в зависимости от весов синапсических связей и порогов.
Граф малопригоден для формальных исследований и компьютерных алгоритмов. Удобнее пользоваться матричным отображением нейросети. Данным способом представления можно отобразить как структуру, конфигурацию, топологию графа, так и численные значения характеристик его синапсических связей.
Составим матрицу следования S (рис.2.8), число строк (и столбцов) которой равно числу нейронов сети, включая нейроны входного и выходного слоя. Каждая строка (и столбец с тем же номером) соответствует одному нейрону. Для удобства установления порядка следования нейронов диагональные элементы матрицы отмечены черным.
Элемент 
![]() синапсической
синапсической 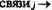
Матрицу S можно изучать в статическом режиме, исследуя и корректируя возможные пути прохождения возбуждений. По этой же матрице в динамическом режиме (моделирования) можно исследовать действительные пути прохождения возбуждений. Такое исследование связано с потактовым расчетом величин возбуждения нейронов.
Нулевые строки (входы) матрицы S соответствуют нейронам входного слоя рецепторам, нулевые столбцы (выходы) нейронам выходного слоя.
Нейроны образуют статические цепочки длины
Нейроны образуют статические цепочки длины т, если существуют синапсические связи (впредь будем опускать слово «синапсические») вида

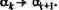
Составляя все статические цепочки по графу G, можно выделить одну или более цепочек максимальной длины. Такие цепочки назовем критическими. (В традиционных многослойных моделях длина критической цепочки совпадает.с числом слоев сети.)
Пусть по статической цепочке i




S транзитивными связями весьма прост.
Алгоритм дополнения матрицы S транзитивными связями весьма прост.
Для всех i = 1, 2,..., N:
i логическим сложением этой строки
Формируем новое значение строки i логическим сложением этой строки со строками, соответствующими не пустым элементам в ней. «Новые* непустые элементы заменяем на непустые элементы, обозначающие транзитивные связи.
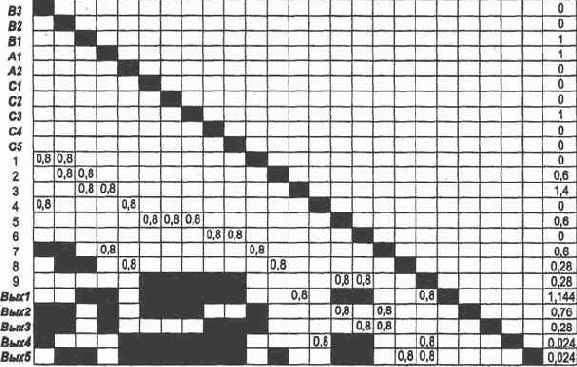
В нашем примере матрица S, дополненная транзитивными связями (непустые клеточки), представлена на рис. 2.8.
Зафиксируем некоторое подмножество R нейронов входного слоя и единственный нейрон г выходного. Построим множество цепочек, ведущих из выделенного подмножества нейронов входного слоя в данный нейрон выходного слоя. Выделенное таким образом множество цепочек назовем статическим путем возбуждения данного нейрона выходного слоя по множеству нейронов входного слоя. Обозначим его R

Представим алгоритм формирования статического пути возбуждения

1. Вычеркиваем из матрицы следования S строки и столбцы, соответствующие нейронам, не принадлежащим R.
2. Вычеркиваем из матрицы следования S все строки и столбцы, отображающие нейроны выходного слоя, кроме нейрона r.
3. Вычеркиваем из матрицы следования S строки и столбцы, отображающие нулевые позиции строки нейрона r.
4. Вычеркиваем из матрицы следования S строки и столбцы, отображающие нейроны внутренних слоев нейросети, в том случае, если в результате предыдущего вычеркивания эти строки оказались нулевыми.
5. Выполняем п. 4, пока не прекратится образование нулевых строк.
На рис. 2.9 матрицей S [B1, A1, C1
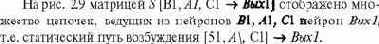
Теперь рассмотрим фактор возбуждения и проанализируем возможные динамические пути прохождения возбуждений.
Динамической цепочкой возбуждений будем называть
Динамической цепочкой возбуждений будем называть статическую цепочку, составленную из нейронов, первые т\ которых обладают отличной от нуля величиной возбуждения.

Динамическая цепочка возбуждений является вырожденной, если ее последний элемент обладает нулевой величиной возбуждения. Вырожденная динамическая цепочка возбуждений характеризует затухание сигнала.
Предъявим сети некоторый образ или эталон (не будет большой ошибки, если и здесь, при предъявлении, мы будем пользоваться словом «образ», ибо все есть образ чегото), приводящий к возбуждению нейроны входного слоя в некоторой конфигурации. Эти нейроны образуют множество R. В результате возбуждения сети оказался возбужденным некоторый нейрон г выходного слоя. Сформировался, таким образом, динамический путь возбуждения R


В общем случае не все нейроны, составляющие статический путь возбуждения, «работают» на возбуждение нейрона выходного слоя, поскольку возможны вырожденные динамические цепочки возбуждения, обусловленные значениями порогов передаточной функции.
Модель механизма запоминания
Главный механизм запоминания, реализованный в природе, можно представить так. Импульс возбуждения, проходя через синапс, «нагревает» и уменьшает его сопротивление, увеличивая синапсический вес. В следующих тактах при последующих предъявлениях эталона импульс возбуждения увереннее одолевает путь возбуждения, с большей определенностью указывая соответствующий образ (как говорится: «Сложилась связь»), а используемые при этом синапсы, «подогреваясь», сохраняют, и, возможно, увеличивают вес.
Здесь работает известное правило Хебба : синапсический вес связи двух возбужденных нейронов увеличивается.
Таким способом даже достигается эффект локализации и максимизации возбуждения на выходном слое, дублирующий, а возможно, исключающий необходимость взаимодействия соседних нейронов.
По видимому, синапсы обладают свойством «остывания» со временем, если нет подтверждения их использования. Такое предположение адекватно свойству нашей памяти: ненужная, не подтверждаемая и не используемая периодически информация стирается («Связи рвутся!»). Стирается до такой степени, что приходится учиться заново.
Отметим и важную роль воображения: эталоны на входном слое поддерживаются достаточно долго, возобновляются или моделируются. Видимо, здесь большое значение имеет эпифиз, «третий глаз» — орган воображения и медитации, память и генератор видений.
При создании искусственных механизмов обучения нейросети возникают вопросы:
увеличивать ли веса всем нейронам, образующим статический путь возбуждения, для запоминания эталона?
увеличивать ли веса только вдоль некоторых (опорных) цепочек статического пути возбуждения?
увеличивать ли веса только нейронов, образующх динамический путь возбуждений, ведь выше предполагалось, что лишь само возбуждение увеличивает вес связи? Зачем возбуждать дополнительные нейроны, если и этих достаточно?
Очевидно, третий аспект в большей степени соответствует самообучению, самонастройке. Вмешательство в наш мозг на этом уровне исключено. Однако система искусственного интеллекта в более выгодном положении. Ведь она находится под нашим неусыпным контролем, реализуя обучение «с учителем», и допускает любое вторжение, корректирующее вынужденные недостатки естественного интеллекта. Поэтому, рассматривая пример (и пытаясь накопить хоть какой то опыт), мы будем увеличивать веса синапсических связей нейронов, составляющих выделенные цепочки статического пути возбуждения от эталона к образу. Назовем такой метод методом опорных путей, который выработан в процессе проведения многочисленных экспериментов. В частности, увеличение синапсических весов большого числа нейронов приводило к неудачам, связанным с корреляцией динамических цепочек возбуждения для разных эталонов и с быстрым насыщением нейросети (недостаток некоторых известных алгоритмов обучения). В процессе обучения многим эталонам рано или поздно все веса сети оказывались повышенными, и она прекращала что либо различать. Начиналась путаница согласно выражению «Ум за разум заходит»
Что же касается величины изменения синапсических весов, то вряд ли необходимо относительно каждого нейрона решать системы дифференциальных уравнений в частных производных. Природа больше рассчитывает на авось, «на глазок» и другие мудрые и практические приблизительные ориентиры, мало привлекательные теоретически. В данном случае нас более обнадеживает «прилив крови» в нужном направлении, стимулируемый информационным раздражителем или легким подзатыльником.
уменьшаемую или увеличиваемую при необходимости.
Введем некую переменную

выверяемую практически (а то и просто единицу), уменьшаемую или увеличиваемую при необходимости.
Таким образом, нам удалось перейти от схемотехники к нейротехнологии, от точного, определенного, к приблизительному, неопределенному. Действительно, не могла эволюция, основанная на принципе «делай все, что можно», методом «проб и ошибок» привести к производству точных электронных схем, упрятанных в черепную коробку. Да и нет в природе точной, абсолютно достоверной информации. Но общие логические принципы и зависимости должны быть воплощены и в той, и в другой технологии.
Нейросетевые технологии и нейрокомпьютеры
Итак, располагая знаниями о данных на входе управляющей системы и реакциях на каждую ситуацию, получаем таблицу. В одном столбце, так называемом запросном поле, — векторситуация, в другом, ответном поле, — принимаемое решение. Такая идея ситуационного управления высказана Д.А. Поспеловым еще в 1970х годах.
Для ее воплощения можно использовать технологии построения ассоциативной памяти, столь широко используемой в современных вычислительных системах. Если между ситуациями ввести операции отношения, то можно построить операции вида «найти ближайшую величину слева (справа)», «найти ближайшие включающие границы» и т.д. Идея ассоциативной ЭВМ давно реализована, например, в STARAN [17] в 1977 г.
На основе вышесказанного строится самообучающаяся система, в режиме обучения дополняющая базу знаний (ту самую таблицу в ассоциативной памяти) с помощью моделирования ситуаций и принимаемых решений, и выдающая решение в рабочем режиме согласно таблице на основе интерполяции.
Однако необходимость выхода на большие размерности ограничивает возможность построения «большой» ассоциативной памяти по существующей технологии. Ведь такая память даже при реализации единственной операции основана на одновременном сравнении входного вектора с запросными частями всех ее регистров и с выдачей содержимого ответного поля в случае совпадения.
Получается, что мозг не может непосредственно хранить таблицы, а моделирует их с помощью нейросетевых механизмов. Исходные предложения, например, Кохонена [13] по применению нейросетей касались именно ассоциативной памяти.
Очевидно, такая реализация не очень удобна, поэтому следует определять области разумного применения каждого средства решения задач искусственного интеллекта.
Рассмотрим, где используется принцип нейросети без расчета, анализа баз знаний и т.д. По видимому, там, где получена первичная информация для органов чувств. На этом же уровне проводим первичную классификацию и принимаем оперативное решение: убежать от стремительно приближающегося автомобиля, надеть противогаз и т.д.
Значит, в нашей жизнедеятельности существует такая ниша, где решение должно быть сверхоперативным, скорее рефлекторным, не допускающим анализа, чему и способствует высокий параллелизм сети. Именно высокий параллелизм наряду с исключением сложных расчетов обусловил взрыв интереса к системам искусственного интеллекта в начале 1980х годов, когда остро встала задача разработки вычислительных средств сверхвысокой производительности.
Здесь мы вновь затронули вопрос актуальности аппаратной реализации нейросети или нейрокомпьютеров , так как программная модель на непараллельном компьютере лишена свойства высокого параллелизма мозга и ограничивает выход на «большие» нейросети.
Указанный параллелизм выражается в том, что одновременно обрабатывается большое число цепочек нейронов. При этом каждый нейрон обрабатывается хотя и по одному алгоритму, но по разным его ветвям: один в конце концов возбудится, другой нет; связи нейрона индивидуальны и изменяются неидентично связям других нейронов и т.д.
Тогда при разработке параллельного вычислительного устройства нейрокомпьютера, способного имитировать работу нейросети высокой производительности, следует учесть нижеперечисленное:
необходимо распределять нейроны (точнее, нейроподобные элементы или соответствующие им программные процедуры) между процессорами НК, синхронизируя обработку нейронов в соответствии с матрицей следования, т.е. реализовать способ распараллеливания по информации;
одинаковые для всех процессоров программы одновременно обрабатываемых нейронов в общем случае должны выполняться по разным ветвям.
При программной реализации нейросети перечисленные
При программной реализации нейросети перечисленные требования соответствуют SPMD технологии («одна программа — много потоков данных»), привлекательность которой обоснована для многих приложений параллельного решения задач высокой сложности.
Привлекательна реализация «большой» нейросети на основе сетевых технологий.
При аппаратной реализации НК (или его аппаратной поддержке) также необходимо учесть требование: один нейроподобный элемент должен делить время между имитацией многих нейронов. Жесткая аппаратная имитация нейросети, соответствующая связи «один нейроподобный элемент — один нейрон», неэффективна, так как ограничивает возможную размерность моделируемой сети.
При применении сетевых технологий в рамках построения более сложных управляющих систем целесообразно использовать НК как сопроцессор под управлением мощного и универсального компьютера — монитора, что обусловлено разнообразными функциями «учителя» по формированию, заданию и регулировке параметров, по обучению и дальнейшему применению результатов. В рамках сегодняшних компьютерных технологий НК должен дополнять персональный компьютер (рабочую станцию) как его внешнее устройство и встраиваться в существующие ОС.
Итак, известны языки логического вывода, экспертные системы, самообучающиеся системы управления, а в природе первично воплощены лишь нейросети.
Почему же средства искусственного интеллекта, опирающиеся далеко не только на одни нейросети, не были первоначально заданы Природой, а явились плодом человеческого гения?
Да просто мозг — конструктивно целесообразен, развиваем, универсален и самодостаточен. С его помощью еще не то можно построить!
Приведем пример колеса: какова должна быть длина нерва, чувствующего обод колеса? Весьма велика. Значит, колесо должно быть отделено от живого существа. И потому человек как существо разумное колесо может сделать сам.
Обобщением «схемотехнического» подхода является подход к построению нейросетей с позиций алгебры высказываний. Логическое описание системы управления или принятия решений, в терминах алгебры высказываний, — «один в один», в результате формирования логической схемы ложится в основу нейронной сети. Остается заменить булевы переменные действительными (достоверная или другие оценки), а операции конъюнкции и дизъюнкции — единой операцией, осуществляемой передаточной функцией нейрона. Конечно, такая замена не столь безболезненна. Необходимы несложные преобразования логического описания, а также настройка порогов и весов связей, чтобы избежать неоднозначности выдаваемых решений.
Кроме того, читатель не должен считать, что каждая нейросеть сводится к однослойной. Значит, предложенный далее алгоритм трассировки нуждается в обобщении, направленном на структуризацию обучаемой нейросети.
Построение нейросети «под задачу»
Мы построили нейросеть с экзотическими (с точки зрения психотерапевта) конъюнкторами и дизъюнкторами.
Предположим теперь (см. рис 2.4, 2.5), что все нейроны одинаковы, реализуют одну передаточную функцию, а веса и пороги реализуют равные и общие возможности.
Введем ту же, но без ограничения по величине возбуждения передаточную функцию
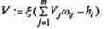
При 
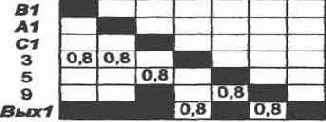
Подадим на вход, например, ситуацию {А1, В2, С3}, требующую решения R1. Величины возбуждений нейронов показаны на рис. 2.6.
На основе расчетов по полученной сети составим табл. 2.1, отображающую правильную (!) работу сети при получении различных решений. При этом связи, предыстория которых определена дизъюнкторами, требуют проверки не более чем одного «представителя»: в рассмотренном примере получаем тот же результат, если вместо C3 положим C1 или C2.
| Таблица 2.1 Примеры расчета принимаемых решений Ситуация | Требуемое решение | |||||
| {A1,B1,C3} | R1 | 1,144 | 0,76 | 0,28 | 0,024 | 0,248 |
| {A1,B2,C2} | R2 | 0,504 | 1,144 | 0,664 | 0,024 | 0,248 |
| {A1,B3,C3} | R2 | 0,504 | 1,144 | 0,664 | 0,504 | 0,024 |
| {A1,B2,C4} | RЗ | 0,504 | 0,664 | 1,144 | 0,024 | 0,224 |
| {A1,B3,C5} | RЗ | 0,504 | 0,664 | 1,144 | 0,504 | 0,024 |
| {A2,B3,C1} | R4 | 0,024 | 0,504 | 0,024 | 1,144 | 0,504 |
Анализируя первые восемь строк таблицы,
Анализируя первые восемь строк таблицы, соответствующие достоверным ситуациям, видим, что по крайней мере максимум возбуждения определяется устойчиво верно.
Рассмотрим ту же неопределенную ситуацию.
Рассмотрим ту же неопределенную ситуацию. Она отражена в последней строке таблицы. Близка ли эта ситуация более всего ситуации, когда Петя направился к Аполлинарии, и надо принимать решение R5 ? Ситуация с Васей, устремившимся туда же, дает примерно тот же ответ.
Отметим, что по убыванию величин возбуждения нейронов выходного слоя вновь полученный результат полностью совпадает с полученным по «схемотехнической» сети (см. рис. 2.5), так что и величина средней прибыли, по видимому, будет близка найденной ранее.
Однако не проще было бы применять способ построения нейросети, близкий к табличному? Что если каждую ситуацию непосредственно «замкнуть» на соответствующее решение, избежав сложной путаницы промежуточных слоев нейронов и не рассчитывая множества вариантов для нахождения максимального возбуждения и распределения возбуждения на выходном слое?
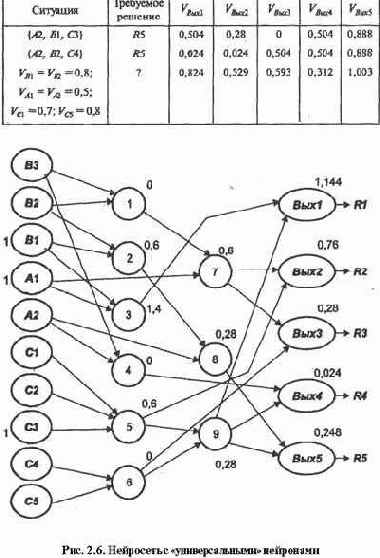
Очень часто на практике так и поступают. Отсюда широкое распространение так называемых однослойных сетей. Построим такую сеть и для нашего примера (рис. 2.7).
Возьмем ту же передаточную функцию с теми же параметрами и рассчитаем те же примеры, отображенные в табл. 2.1. Составим для них табл. 2.2.
Таблица 2.2 Примеры расчета решений по однослойной нейросети

Данная нейросеть также оказывает предпочтение
Продолжение
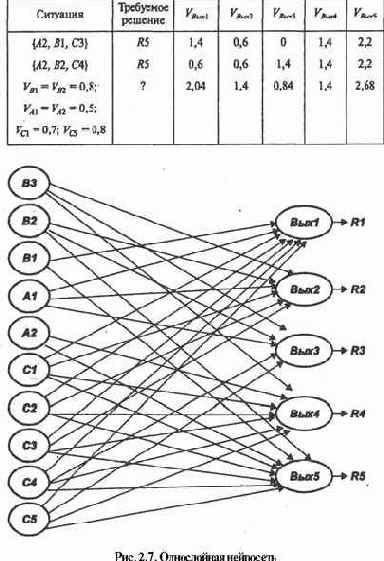
Данная нейросеть также оказывает предпочтение решению R5, хотя порядок убывания величин возбуждения выходного слоя отличен от ранее полученного. Предпочтительность решений R2 и R3 меняется местами.
Очевидно, что масштабирование порогов позволяет управлять величинами возбуждений, и при желании можно добиться аналогичных результатов расчетов по этим двум сетям. Но надо ли?
Рассмотрим пример, навеянный временем перестройки.
Рассмотрим пример, навеянный временем перестройки.
Вася и Петя — друзья. Обозначим А — множество друзей:
А = {А1, А2} = {Вася, Петя}.
Вася и Петя создали «крышу», под которой успешно трудится ряд палаток:
заботливо опекаемые хозяйками, соответственно Оксаной и Роксаной, Мариной и Региной, а также Аполлинарией. Палатки реализуют продукцию фирм:
Фирма Красный киллер производит винноводочную продукцию отличного качества. Фирма Пират специализируется на аудио и видеопродукции и других культурных ценностях, а фирма Ночная бабочка — на французской косметике из мосластых московских дворняг.
Ситуацию контролирует дядя Рамзай из налогового ведомства, который имеет свой маленький частный бизнес. С каждой сложившейся ситуацией, определяемой тем, кто из друзей какие палатки посетил и чья продукция находилась на реализации, дядя Рамзай связывает свою долю прибыли, основанную, мягко говоря, на шантаже. Дядя Рамзай имеет свой штат осведомителей: пару бомжей жертв предыдущей амнистии, и парутройку голопузых апологетов трудного детства, которые с некоторой долей достоверности доставляют ему информацию.
Дядя Рамзай — прогрессивный бизнесмен, и оценки прибыли производит с помощью математического аппарата, обратившись за помощью к нам. А информации дяде Рамзаю приходится обрабатывать много. Он, прямо скажем, работает в условиях неопределенности и усиленных помех. Судите сами. Оксана делит любовь между Васей и Петей. Роксана — пока нет. Марина и Регина, жалея, подкармливают юных следопытов. Аполлинария заполучила покровителя в местной мэрии и разъезжает в длиннющем "линкольне". Тщетно пытаясь разрушить узы бескорыстной дружбы, фирма Пират подкупила Васю, снизив нагрузку вымогательства на свою продукцию. Петя, кажется, пошел на нарушение «закона» и вторгается в область, контролируемую конкурентами. Все такие обстоятельства прямо или косвенно влияют на долю прибыли дяди Рамзая.
А мы, принимая заказ на
А мы, принимая заказ на очень трудно формализуемую задачу, хотим уяснить, что нужно дяде Рамзаю, и устанавливаем:
он хочет, задавая исходные данные на основе неполной или недостоверной информации своих агентов, всетаки распознать с наибольшей определенностью, что это за ситуация и на какую прибыль можно рассчитывать;
он хочет, задавая исходную ситуацию с некоторой достоверностью, установить среднюю величину прибыли;
он хочет сделать вывод о частоте появления различных ситуаций, чтобы перераспределить таксу за молчание о шалостях Васи и Пети.
Итак, абстрагируемся. Пусть по стечению обстоятельств, которые мы будем называть событиями, принимаются решения R1, R2, R3, R4, R5.
События выражаются записями, например, вида {A1, B2, С3} Это означает, что Вася (А1) отправился в палатку Марины {СУ), торгующей в этот раз продукцией фирмы Пират
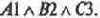
Решения образуют конечное множество. Каждое решение носит сугубо личностный характер и определяет тактику дальнейшего поведения, надежду на существенное приобретение, тур поездку и т.д. Одно решение соответствует некоторой, в общем случае не единственной, комбинации событий. Для изображения таких комбинаций воспользуемся записями, например, вида
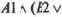
Это означает, что Вася отправился в палатку то ли к Регине, то ли к Аполлинарии, торгующей продукцией то ли фирмы Пират, то ли фирмы Ночная бабочка. Однако эта же запись означает, что все составляющие ее конъюнкции и другие приводят к одному и тому же решению.
и перебрав все возможные ситуации,
Проанализировав и перебрав все возможные ситуации, с учетом одинакового принимаемого решения получим систему логических высказываний — предикатов как основу формализации задачи при построении нейросети:

Тогда, например, первое логическое высказывание означает: «Если Вася отправился в одну из пяти палаток, и все они торгуют сегодня продукцией фирмы Красный киллер, то следует принять решение R1 (например, заказать туристическую путевку)».
Второе логическое высказывание означает: «Если Вася посетил одну из палаток С1, С2 или С3, торгующих сегодня продукцией фирм B2 и (или) B3, то следует принять решение R2» и т.д.
Применение типовых нейросетей
Справедливо желание построения универсальных моделей нейросетей в составе программного обеспечения компьютера, снабженных механизмами приспособления под задачу пользователя. Е1це более справедливо желание построить набор аппаратных средств — нейросетей (нейрокомпьютеров, НК), сопряженных с компьютером и, по выбору пользователя, участвующих в решении сложных задач. Такие аппаратно реализованные нейросети, как приставки или внешние устройства компьютера, например, определяют специальное направление использования ПЛИС интегральных схем с программируемой логикой.
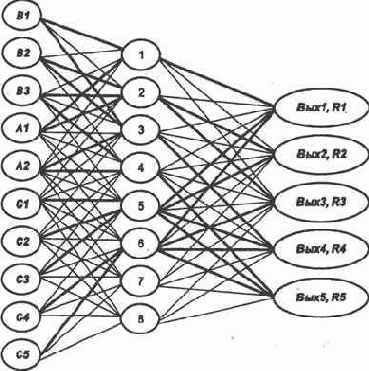
Однослойная нейросеть. Для наглядности воспользуемся как матричным, удобным алгоритмически, так и графическим представлением нейросети.
Однослойная нейросеть, составленная по принципу «каждый с каждым», представлена на рис. 2.10. Пусть используется предложенная выше передаточная функция
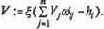
Значения

![]() положим равными нулю.
положим равными нулю.
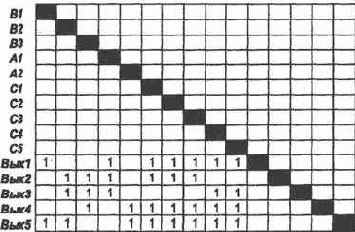
Закрепим 10 нейронов входного слоя за исходными данными, 5 выходов — за решениями. Этим мы выделим интересующую нас подсеть, которой соответствует матрица следования на рис. 2.11. Здесь отображен ее окончательный вид, так как сначала все веса связей принимаются равными нулю.
Для того чтобы сформировать решение R\ на нейроне Вых\, надо значительно увеличить веса связей этого нейрона с нейронами В1, А1, С1, С2, С3, С4, С5, т.е. построить статический путь возбуждения [B1, А1, С1, С2, С3, C4, C5]

Установим веса связей между нейронами В1, А1, С1, С2, С3, C4, C5, с одной стороны, и нейроном Вых1 — с другой, равными единице, оставив нулевыми веса связей этого нейрона с другими нейронами входного слоя. Таким образом, полностью исключается влияние других нейронов входного слоя на данный выходной нейрон. Конкретная задача может потребовать корректировки, учета взаимного влияния всех входных ситуаций в результате тщательного экспериментального исследования задачи.
Здесь вновь прослеживается преимущество нейросети,
Здесь вновь прослеживается преимущество нейросети, способной элементарно учитывать наблюдаемые или интуитивно предполагаемые поправки, требующие огромных исследований и расчетов.
Поступив так же со всеми выделенными нейронами выходного слоя, получим окончательный вид матрицы следования (см. рис. 2.11). Построенная нейросеть полностью соответствует специальной сети «под задачу», представленной на рис. 2.7.
Так какую же сеть предложить
Так какую же сеть предложить дяде Рамзаю? Ведь надо и подоходчивее, и попрактичнее, но и так, чтобы не казалось уж слишком просто.
Нейросеть произвольной структуры. Предположим, мы располагаем некоторым банком «красиво» изображенных графических схем, которые можно положить в основу структуры нейросети. Понравившуюся структуру интерпретируем как нейросеть, дополнив ее передаточной функцией и обучив решению задачи, поставленной дядей Рамзаем.
Пусть выбранная нейросеть имеет 12 входов (более чем достаточно), 5 выходов и реализует ту же передаточную функцию с начальными значениями весов

Однако сеть обладает специфической топологией,
Однако сеть обладает специфической топологией, затрудняющей ее обучение. Сеть многослойная, что исключает связи «через слой», присутствующие, например, в сети на рис. 2.6, как результат построения нейросети «под задачу».
Применим метод опорных путей, или трассировки, расширяющий использованный выше «схемотехнический» подход. Его можно изобразить схемой рис. 2.1
Суть метода в трассировке соединений, в назначении высоких весов некоторых связей, превращающих нейросеть в законченное функциональное устройство. При такой трассировке обучение производится на эталонах в полном смысле этого слова на вполне определенных (достоверных) ситуациях, например на отсутствии события (0) или на его наступлении (1). После обучения сеть должна выдавать наиболее близкое решение при недостоверной информации, т.е. согласно вероятности наступления того или иного события. Хотя, как показано на примерах, можно выйти и за рамки теории вероятности, не требуя полноты множества событий и условия нормировки, но взвешивая события на основе какихто других принципов.
Итак, для успешной, наглядной и легко рассчитываемой трассировки решим вопрос кардинально: какие веса полагать равными нулю, а какие — единице?
Все прочие возможности, например min

введение порога h = 0,5 и т.д., будут способствовать более плавной работе сети, непрерывности перехода из состояния в состояние.
и эвристики, выполним трассировку нейросети
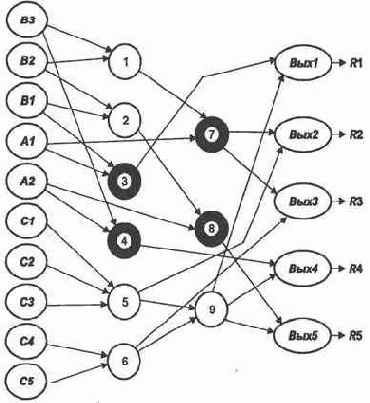
Применив принципы комбинаторики и эвристики, выполним трассировку нейросети (рис. 2.12). На рисунке наглядно показано, какая нейросеть была предоставлена, насколько она «неповоротлива», скажем, по сравнению с однослойной «каждый с каждым».
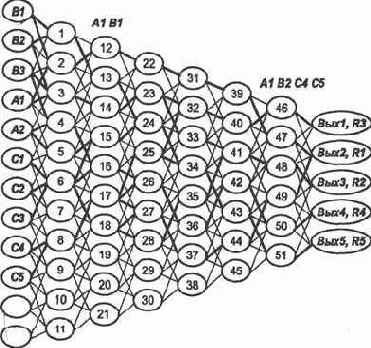
Далее рассмотрим формальный алгоритм трассировки. Однако чтобы настроиться на его понимание, необходимо проанализировать свои действия и сделать следующие выводы.
Мы исследовали слой за слоем,
1. Мы исследовали слой за слоем, постоянно помня о цели — пять комбинаций ситуаций, каждая из которых должна возбудить один из нейронов выходного слоя. Причем решения за этими нейронами пока жестко не закреплены.
2. В каждом слое мы собирали частную комбинацию терм, который можно использовать в последующем, — из доступных термов предыдущего слоя.
3. Термы, которые пока не используются при конструировании изза их взаимной удаленности, мы запоминали без изменения на анализируемом слое, пытаясь «подтянуть» их в направлении возможного дальнейшего объединения.
4. Мы старались не «тянуть» термы «поперек» сети. В противном случае возникла бы проблема — как избежать пересечений и искажения уже сформированных термов. Все это заставило нас долго не закреплять нейроны выходного слоя за решениями, что в конце концов привело к нарушению естественного порядка следования решений.
Для автоматизации трассировки необходимо матричное представление, только и доступное компьютеру.
Матрица следования, отражающая трассировку нейросети, получается на основе рис. 2.12, если отметить элементы, соответствующие «тонким» линиям, нулевыми весами, а элементы, соответствующие «жирным» линиям, — весами, равными единице.
На рис. 2.13 отражен динамический путь возбуждения, приводящий к решению R1. Он строится по алгоритму, изложенному в подразд. 2.5. В данном случае динамические пути возбуждения совпадают со статическими. В общем случае из статического пути возбуждения необходимо исключить нейроны, которым соответствуют нулевые строки матрицы следования.
Аналогично получают динамические пути возбуждения, приводящие к другим решениям.
Поставим теперь задачу дальнейших исследований: как построить все необходимые пути возбуждения так, чтобы они, возможно, пересекались, но только для формирования общих термов? А способна ли выбранная нами «готовая» нейросеть вообще справиться с поставленной задачей или предпочтительнее принцип «нейросеть под задачу»?

Рекомендации
Испытывая различные структуры нейросети и пытаясь произвести обучение рассматриваемой задаче, мы, в частности, много усилий затратили на одну нейросеть. Выяснилось, что 5 9 имеет место пересечение путей возбуждения несовместимых ситуаций, требующих максимальных возбуждений разных нейронов выходного слоя. Нам так и не удалось разнести эти пути возбуждений. Коррекция весов одного пути немедленно вызывала коррекцию возбуждения другого. Кроме того, при «случайной» топологии сети величины возбуждения нейронов входного слоя оказывали различное влияние на возбуждение нейронов выходного.
В результате предпочтительнее оказалась регулярная структура сети, принудительное навязывание структуры и контроль взаимодействия ее элементов.
Другой важный вывод касается порочности излишней «экономии» при формировании нейросети.
Почему мы эвристически решали столь трудную комбинаторную задачу согласно рекомендациям, без всякого конструктивного алгоритма?
Наверное, изза отсутствия должной избыточности. Умышленно создавая головоломку, мы теснились на маленькой сети с ограниченными связями. Таковы ли условия в живой природе, где складывающиеся связи помимо запоминания удовлетворяют требованиям устойчивости, надежности, дублирования — резервирования и хд.? Здесь уж либо жалеть и экономить, рискуя оказаться перед неразрешимостью задачи вообще, либо щедро и самым простым способом, по возможности независимо, прокладывать цепочки возбуждений от каждого нейрона входного слоя к каждому «заинтересованному» нейрону выходного слоя. Нет, ясность мышления основана на достаточности и даже избыточности мыслительной субстанции.
Снимем некоторые ограничения и рассмотрим другую типовую нейросеть. На рис. 2.14 тем же методом трассировки опорных путей показано возможное решение задачи. Здесь входной и первый внутренний слои сети связаны почти по принципу «каждый с каждым», что и позволило сформировать основные конструкции — термы, на основе комбинаций которых затем продолжается создание нужных путей возбуждения.
Все построения ведутся на основе рекурсивного подхода: сначала мы имеем термы самого низкого уровня — на входном слое, на их базе получаем конструктивные единицы первого уровня, их комбинируем в термы более высокого уровня и т.д. Конечно, это самое конструктивное решение (мышление). Ведь термы могут формироваться в коре для многократного и многоцелевого использования, так сказать, впрок.
возбуждений от нейронов входного слоя
Но возможен и другой, более «щедрый» путь: «тянуть» цепочки «сильных» возбуждений от нейронов входного слоя к нейронам выходного слоя, избегая пересечений.
Пропагандируемая нами случайнорегулярная структура связей не должна зависеть от «слоистости» сети: связи «через слой» значительно упрощают пути возбуждения нейронов.
и последующая замена булевых функций
Вместе с тем «схемотехнический» подход и последующая замена булевых функций л и v одной передаточной функцией приводят к интересной гипотезе.
Оптимальное число слоев нейросети или максимальная длина статической цепочки (если принцип «слоистости» не актуален) совпадает с максимальной длиной логической цепочки в аналогичной электронной схеме, реализующей систему булевых функций зависимости выходных сигналов — аналогов возбуждения нейронов выходного слоя от входных сигналов — аналогов возбуждения рецепторов.
Сказанное позволяет ставить задачу минимизации длины статической цепочки при формировании нейросети для максимального упрощения ее структуры. Этим определяется широкая возможность применения однослойных сетей в том случае, когда задача сводится к обработке простых таблиц с однозначным соответствием принимаемых решений совокупности исходных ситуаций.
Однако дело в том, что любая булева функция представима дизъюнктивной нормальной формой, т.е. дизъюнкцией известных специалисту в области математической логики и схемотехники конъюнкций. Значит, соответствующая электронная схема состоит из логических цепочек, длина которых равна двум. При построении таких схем условно выделяют два уровня: на первом уровне формируются конъюнкции на основе комбинаций булевых переменных и их отрицаний, а на втором уровне — их дизъюнкция.
Таким образом, при использовании «схемотехнического» подхода для построении обученных нейросетей в самом общем случае мы можем довольствоваться не более чем двухслойными нейросетями.
Действительно, в нашем примере каждое событие, требующее определенного решения, интерпретируется как конъюнкция элементарных событий (например, и в более доходчивой форме соответствует логической операции И. Комбинация событий, приводящих к одному решению, соответствует объединению дизъюнкции событий (например, к решению R1 приводит дизъ
Электронная схема на основе логических высказываний, приведенных выше, которую легко себе представить, отличается от изображенной на рис. 2.1. В ней все длины логических цепочек равны двум. Следовательно, при замене логических элементов нейронами, выполняющими пороговую передаточную функцию (при замене булевых переменных действительными), получаем статические цепочки нейросети также с длинами, равными двум.
Значит, принципиально возможно априорное ограничение: «для построения схемы обученной нейросети для заданного применения изображаем два слоя (не считая рецепторного) нейронов, причем один из них выходной. Далее, только лишь выбором конфигурации связей, возможно, через слой, достигаем требуемой функциональной ориентации нейросети».
Неужели достаточно иметь дело с одно и двухслойными нейросетями? Над этой проблемой советуем читателю подумать самостоятельно, обратив внимание на переход от схемы на рис. 2.1, преобразующей булевы переменные, к идентичной структуре нейронной сети на рис. 2.6, обрабатывающей действительные переменные.
«схемотехнический» подход к построению нейросети «под задачу»
Реализуем подход, используемый при построении схем устройств ЭВМ и другой электронной техники. Выделим функционально полную для данного применения систему булевых функций — дизъюнкцию

![]()
Нарушив принятые обозначения, построим (рис. 2.1) схему, реализующую алгоритм счета значения выражения (2.1). Предполагаем подавать на вход значения булевых переменных, обозначающих события.
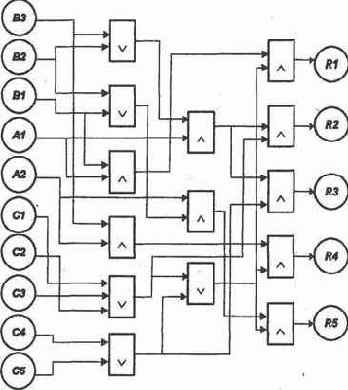
Такая электронная схема могла бы
Такая электронная схема могла бы нам верно служить, способствуя быстрому определению необходимой реакции на сложившуюся ситуацию, если мы предусмотрели все возможные ситуации, знаем, какое решение соответствует каждой из них, и всегда обладаем полной и точной информацией о происходящих событиях. Но ведь не зря мы обращаем внимание на те помехи и неопределенность, в условиях которых приходится жить и работать. Мы должны оперировать только достоверностями либо другими оценками событий, пытаясь определить, какой ситуации более всего соответствуют сложившиеся обстоятельства.
Значит, мы должны из точного, детерминированного представления перейти в область ассоциативного, неточного, приблизительного мышления! Но степень (частота) угадывания должна быть достаточно высока.
Именно здесь помогает нейросеть.
Прежде всего надо перейти от типа булевых переменных к типу действительных, введя в обращение не непреложность событий, а лишь вероятности или другие весовые оценки их наступления (электронной технике это не свойственно.) Затем необходимо реализовать аналоги булевых функций над этим новым типом данных, т.е. заставить нейроны с помощью весов, порогов и самой передаточной функции выполнять дизъюнкции и конъюнкции с учетом вариации и неопределенности данных. При этом абсолютно достоверные данные, несомненно, приведут к известным решениям, а по неточным данным можно определить лишь вес каждого из возможных решений. Тогда по максимальному весу определим, на что более всего похожа данная неопределенная ситуация.
Выберем передаточную функцию произвольного (/го) нейрона с числом т входов — дендритов:
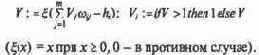
Здесь как всегда, величина возбуждения. Тогда нейронконъюнктор может быть реализован с помощью существенно высокого порога (рис. 2.2), где значение

При обучении предполагается, что входные сигналы булевы переменные, принимающие значения 0, 1. Положим выберем

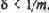
Тогда для преодоления порога на
Тогда для преодоления порога на всех входах должны быть 1; недостаток хотя бы одной 1 приведет к тому, что взвешенная сумма будет более чем на
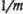
При переходе к действительным переменным, когда вместо событий рассматриваются, например, лишь предполагаемые вероятности их наступления, экспериментальный выбор значения 8 может обусловить ту границу, когда считаться с возможностью данной комбинации событий нецелесообразно.
Нейрон дизъюнктор реализуется, наоборот, при
Нейрон дизъюнктор реализуется, наоборот, при низком значении порога, но при высоких значениях весов. Порог выбирается так, чтобы уже при возбуждении на одном входе возникал сигнал возбуждения на выходе. При этом сигнал на выходе не превышает «1» (рис. 2.3).
Понятно, что при полной определенности в режиме обучения возбуждение поступает по единственному входу (нейрон реализует функцию «ИСКЛЮЧАЮЩЕЕ ИЛИ»). В условиях неопределенности предполагается, что нейрон имитирует выполнение функции ИЛИ, допуская возбуждение более чем на одном входе.
Итак, поменяем тип данных и заменим нейронами все элементы на схеме рис. 2.1. Получим нейросеть (рис. 2.4), где нейроны конъюнкторы заштрихованы.
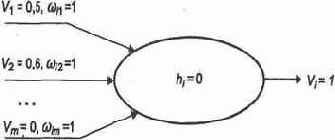
Теперь позволим дяде Рамзаю поучиться, поэкспериментировать, задавая различные достоверности событий — возможных или невозможных. Например, зададим «правильную» и абсолютно достоверную ситуацию
B3=1,A1=1,C4=1 (Вася отправился к Регине, торгующей ямайским ромом).
в первом такте возбудятся нейроны
Легко проследить, что в первом такте возбудятся нейроны 1 и 6, реализующие дизъюнкцию. Величина их возбуждения равна 1. В следующем такте возбуждение нейронов 1, 6 и A1 приведет к возбуждению (с величиной, равной 1) нейронов 7 и 9, а в следующем такте сигналы возбуждения нейронов 6 и 7 поступят на вход нейрона конъюнктора ВыхЗ. Никакой другой нейрон выходного слоя не возбудится.
Рассмотрим другую ситуацию, неопределенную и недостоверную.
Пусть то ли Вася, то ли Петя — «разведчик» не установил точно — направился то ли к Оксане, то ли к Аполлинарии, торгующим в этот день то ли тройным одеколоном, то ли золотым диском группы «Тарарам».
Дядя Рамзай по выданной нами инструкции решает использовать интуитивные оценки веса, или, на нашем языке, оценить достоверность каждой компоненты возникшей ситуации. Поскольку прогулки как Васи, так и Пети одинаково достоверны, то дядя Рамзай полагает величину возбуждения нейронов
А1 и А2, равной 0,5

После долгих раздумий он по наитию полагает




Напоминаем еще раз, что требовать полноты множества событий и непременного выполнения нормировочного условия не обязательно. Достоверность может выбираться по наитию, на уровне чувств. Именно эти качества неопределенности, субъективности, наличия жизненного опыта и интуиции присущи механизмам ассоциативного мышления.
мы установили веса всех конъюнкторов
Сдавая нейросеть «в эксплуатацию», мы установили веса всех конъюнкторов равными 0,5, а дизъюнкторов, — равными 1. Пороги конъюнкторов определяются значением

Важность данного примера требует повторения рисунка нейросети (рис. 2.5) с проставленными возле нейронов значениями сигналов возбуждения. В итоге ситуация скорее всего имеет решение R5 и уж никак не R4. Однако ситуация, соответствующая решению R1, требует внимания и т.д.
Пусть при вполне определенной ситуации
Пусть при вполне определенной ситуации (все достоверности принимают значение «1») каждое решение Ri приносит прибыль


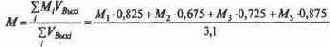
Конечно, полученное решение столь же неопределенно, как и карточный расклад, что предвещает трогательную встречу в казенном доме, поэтому мы погружаемся в дальнейший поиск.
Возбуждение входного слоя
Определим теперь возбуждение входного слоя, учитывая то, что по нейросетевым технологиям решаются сложные, чаще всего трудно формализуемые задачи. Исходная информация этих задач может быть настолько несовместима по смыслу, типам данных и единицам измерения, что приведение ее к некоторому количественному воплощению — величине возбуждения нейронов входного слоя — представляет серьезную проблему.
Например, как объединить величину превышаемой водителем скорости, тип автомобиля иностранного производства со вчерашним неудачным выступлением любимой автоинспектором футбольной команды при нахождении величины штрафа? Ведь каждый из перечисленных факторов должен определить некоторые общие, приведенные значения возбуждения.
Такое приведение также зависит от задачи. Поскольку нейроны — нечто стандартное для данной задачи или класса задач, то каждая характеристика нейрона — величина возбуждения, веса его синапсических связей, порог, передаточная функция — должны быть одинаковы или принадлежать общему (по каждой характеристике) для всех нейронов диапазону возможных значений.
Дадим рекомендации, основанные на «событийном» принципе.
В нашем новом примере о превышении скорости разобьем скорость на диапазоны штрафования, например
[90,100), [100 — ПО), [ПО 120), [120 200].
За каждым диапазоном скорости закрепим нейрон входного слоя — рецептор. Определим его среднее значение возбуждения, равное 1. Пусть отклонение к границам диапазона скорости пропорционально уменьшает эту величину возбуждения, увеличивая величину возбуждения рецептора «соседнего» диапазона. Другой вариант задания исходных данных основан на решении вопроса принадлежности скорости некоторому диапазону. Тогда величина возбуждения превратится в булеву переменную, фиксируя событие. Но более универсальный подход основан на связывании величины возбуждения рецептора с достоверностью — вероятностью того, что величина скорости принадлежит одному или нескольким диапазонам. Такой подход мы и намерены воплотить в дальнейшем.
А именно хотя бы интуитивно (ведь интуиция основана на опыте), определим достоверность того, что интересующая нас величина принадлежит данному диапазону. С какой достоверностью она принадлежит второму диапазону? А третьему? Можно даже уйти от понятия достоверности как вероятностной категории. Все ли мы знакомы с понятием полноты множества событий? Ведь часто слышим: «Даю голову на отсечение, что это так, хотя и допускаю, что все наоборот...». Главное, чтобы исходные оценки информации были относительными, отражающими принцип «больше — меньше». Это расширит популярность нейротехнологий, исключит необходимость специальных знаний. Ведь какието начальные возбуждения рецепторов при их относительном различии распространятся по нейросети, определяя предпочтительность принимаемого решения.
Тогда на этапе обучения нейросети получим возможность формирования аналога некой таблицы, в соответствии с которой будет действовать инспектор. (Однако здесь пока не рассматривается процесс обучения нейросети — формирование этой таблицы, а только принцип формирования данных для входа в нее.)
Выделим нейроны, «отвечающие» за типы автомобилей: отечественного производства, «мерседес», «вольво», джип «чероки» и т.д. Величину возбуждения этих нейронов будем полагать равной 1 (на этапе обучения) или равной достоверности события (в рабочем режиме). Аналогично выделим рецепторы, «отвечающие» за другие возможные события: степень интеллигентности водителя (так же по диапазонам изменения), выигрыш или проигрыш любимой команды и т.д.
Следовательно, на входном слое будут формироваться приведенные значения возбуждения.
В рабочем режиме мы, таким образом, получили возможность использования неопределенной, недостоверной информации. Например, инспектор не смог изза высокой скорости отличить «ниву» от джипа «чероки». Тогда он решает ввести значение 0,5 в графу «нива» (величина возбуждения рецептора, «отвечающего» за «ниву» станет равной 0,5) и 0,5 — в графу джип «чероки» (такой же станет величина возбуждения соответствующего рецептора). Однако, подумав, он на всякий случай вводит величину 0,2 в графу ВАЗ2104, что также во власти его сомнений. Так же инспектор поступает и с другими характеристиками сложившейся ситуации в поисках наиболее достоверного решения по принципу наибольшей похожести.