Булева концепция алгебры высказываний о событиях
" Ученые объяснения большей частью производят то впечатление, что бывшее ясно и понятно становится темно и запутанно".
Определение 1. Предполагаемое или свершившееся действие, его фигурант, результат, а также условия свершения, называются событием.
Определение 2. Событие выражается высказыванием о его свершении.
Высказыванию о событии (далее - просто высказывание, считая событие и высказывание о нем синонимами) можно поставить в соответствие переменную, которая в рамках булевой концепции может принимать значение ИСТИНА (1) или ЛОЖЬ (0).
Например:
x = <поезд опоздал на пять минут>; y = <в данной операции принимал участие Вася> (достаточно сообщить лишь имя); z = <скорость автомобиля принадлежит диапазону (120-140 км/ч)> (достаточно кратко обозначить диапазон в известном контексте, как условие свершения некоторого действия, приведшего к автокатастрофе).
Очевидно, что каждая переменная x, y, z может принимать одно из двух значений - 0 или 1.
Над высказываниями производятся логические операции. В рамках последующих построений потребуются четыре операции: отрицание (¬x, НЕx, x ), конъюнкция (



Предполагая достаточные знания слушателей, можно напомнить:
одноместная операция отрицания меняет значение переменной на противоположное; двуместная операция конъюнкции над двумя и (рекурсивно) более переменными порождает значение 1 тогда и только тогда, когда все переменные имеют значение 1; двуместная операция дизъюнкции над двумя и (рекурсивно) более переменными порождает значение 1, когда хотя бы одна переменная имеет значение 1; переменная справа от знака операции следования (импликации) принимает значение 1 тогда и только тогда, когда выражение слева от этого знака имеет значение 1.
Кроме того, ниже используется операция ИСКЛЮЧАЮЩЕЕ ИЛИ, предполагающая возможность лишь единственного вхождения переменной со значением 1 в операцию дизъюнкции, объединяющую несколько переменных.
Переход от высказываний к их булевой интерпретации, к булевым переменным, вводит в действие все законы, свойства и правила эквивалентных преобразований, известные из булевой алгебры.
Закон коммутативности:
 | (1.1) |
 | (1.2) |
 | (1.3) |
 | (1.4) |
 | (1.5) |
 | (1.6) |
 | (1.7) |
 | (1.8) |
 | (1.9) |
 | (1.10) |






Переход от высказываний к их булевой интерпретации, к булевым переменным, вводит в действие все законы, свойства и правила эквивалентных преобразований, известные из булевой алгебры.
Закон коммутативности:
 | (1.1) |
 | (1.2) |
 | (1.3) |
 | (1.4) |
 | (1.5) |
 | (1.6) |
 | (1.7) |
 | (1.8) |
 | (1.9) |
 | (1.10) |






Достоверность высказываний о событиях
Говоря о высказываниях как о логических переменных, мы, несомненно, предполагаем наличие субъективного фактора: ведь это кто-то сказал. И мы говорим верному другу: "Я мало доверяю этому человеку, но он сказал …, а дыма без огня не бывает".
Очевидно, недостаточно резких, кардинальных, взаимоисключающих, крайних суждений о высказываниях, подразделяющих их на истинные и ложные. Жизненный опыт говорит, что стопроцентной правды не бывает.
Таким образом, необходимо ввести понятие достоверность высказывания, которая идеально представляет вероятность того, что данное высказывание о свершении события истинно, т.е. представляющая его логическая переменная равна 1.
В этой оценке достоверности вновь практически преобладает субъективный фактор. Поэтому при построении экспертных систем применяется двойная оценка: оценка, данная экспертом по запросу, и вес самого эксперта. Здесь эффективно используется аппарат нечетких множеств [30].
Говоря о сложных высказываниях, отображаемых деревьями логических возможностей, тем более трудно судить о достоверности высказываний о событиях, особенно тех, которые отображаются концевыми вершинами.
Рассмотрим пример. Информатор сообщает Агенту о том, что видел своими глазами, как Марина передала Васе пачку денег. Призвав на помощь свой богатый опыт, Агент рассуждает логически:
Насколько можно доверять Информатору, который три дня не брился и от которого дурно пахнет?Мог ли находиться Информатор в это время в нужном месте, чтобы "видеть своими глазами"?Насколько верно то, что в переданной пачке были деньги?Можно ли оперативно воспользоваться существующими математическими методами оценки (например, аппаратом нечетких множеств), заодно учитывающими другие факторы, как, например, личные финансовые трудности, или необходимые оценки следует выполнить интуитивно, "с потолка"?Так какова же должна быть формулировка отчета в Центр для получения максимального вознаграждения за поимку взяточника?
Таким образом, видно, что оценка достоверности высказываний неизбежна, но представляет значительные практические трудности, тем более - при требуемой оперативности этих оценок, столь важной в реальных системах управления и принятия решений.
Итак, на основе алгебры высказываний можно создавать электронные системы принятия решений: на входе задавать ситуацию, на выходе получать указание на правильную реакцию. Все дело лишь в интерпретации предметной области - во вскрытии причинно-следственных связей, в исследовании личного или коллективного опыта, в изучении теории. Необходимы и схемотехнические навыки запоминания связей.
Однако смущают два обстоятельства:
Неопределенность исходной информации о ситуациях, исключающая точный ответ на вопрос о наличии или отсутствии события и делающая неправомерным использование исключительно булевых переменных. Высказывания не бывают истинными и ложными, как это предполагается в классической математической логике. Высказывания оцениваются своей достоверностью, которая принимает действительные значения на отрезке [0, 1] и подчиняется известным положениям теории вероятности.Способность человека логично мыслить на неформальном уровне не реализуется с помощью конъюнкторов и дизъюнкторов в составе мозга. Именно вскрытие механизмов мышления, особенно того, которое мы называем рефлекторным, привлекает внимание исследователей. Необходимо искать механизмы мышления, оперирующие не с булевыми переменными, а с действительными, несущими смысл достоверности.
Пусть рассмотренные выше переменные-высказывания {xi}, образующие факторное пространство, могут принимать значения достоверности {Pi}, 0


Так как факторное пространство формируется на основе исчерпывающих множеств событий, то внутри каждого такого множества выполняется известное правило нормировки: сумма достоверностей событий каждого такого множества равна единице.
Перегруппируем события и дополним дерево логических возможностей, представленное на рис. 1.1, указав на его ветвях (стрелках), в качестве весов этих ветвей, значения достоверности событий (рис. 1.5). Получим вероятностное дерево логических возможностей.
При организации ветвления в этом дереве также предполагаются все возможные альтернативы, т.е. исчерпывающие множества событий.
Поэтому сумма вероятностей всех событий, отображаемых вершинами, которые связаны входящими стрелками, исходящими из некоторой вершины, равна единице.

Рис. 1.5. Вероятностное дерево логических возможностей
В отличие от дерева логических возможностей, вероятностное дерево явно отображает зависимость событий. События, зависимые от данного, отображаются более низкими уровнями ветвления. Такая зависимость определяется на уровне смыслового анализа факторного пространства.
Например, логично предположить, что формы труда, отдыха и спортивных развлечений зависят от времени года, затем - от распорядка приема пищи. Такая зависимость и отображается на рис. 1.5.
Тогда достоверность событий формируется с помощью условных вероятностей, зависящих от путей, по которым достигаются эти события. Поэтому на вероятностном дереве логических возможностей целесообразно повторять вершины одного смыслового содержания, в результате чего размножаются варианты ветвления, а дерево существенно разрастается. От совмещения путей страдает наглядность, и не более того.
Чтобы найти вероятность некоторого события b при условии свершения события а (событию а может соответствовать корневая вершина, тогда речь идет о полной, а не условной вероятности), необходимо найти все пути, ведущие из a в b. По каждому пути необходимо перемножить все веса ветвей. Полученные по всем путям произведения необходимо сложить.
Пример 1. Найдем вероятность того, что отдыхающий весной и летом в произвольно выбранный момент времени совершает прогулку верхом:
0,25 ? 0,33 ? 0,5 ? 0,4 + 0,25 ? 0,33 ? 0,3 = 0,04125.
Пример 2. Найдем вероятность того, что в произвольно выбранный момент времени в течение года отдыхающий совершает прогулку верхом:
0,25 ? 0,33 ? 0,5 ? 0,4 + 0,25 ? 0,33 ? 0,3 + 0,25 ? 0,33 ? 0,2 = 0,05775.
Исчерпывающее множество событий
Следующие ниже определения не могут не затронуть смысловых особенностей высказываний о событиях. Кроме чисто формальных свойств высказываний, выражающихся в их истинности или ложности, невозможно полностью абстрагироваться от содержательной сути или от контекста, в котором они звучат.
Определение 4. Исчерпывающее множество событий (ИМС) образуют те события, совокупность высказываний, о которых покрывает весь возможный смысловой диапазон проявления объекта высказывания, и каждая допустимая ситуация характеризуется тем, что значение ИСТИНА (1) может принимать единственное высказывание из этой совокупности. (Значение 0 могут принимать все высказывания.)
Рассмотрим примеры.
В состав редколлегии входят трое: Иванов, Петров, Сидоров. Тогда провозглашение фамилий этих фигурантов определяет исчерпывающее множество событий при выдвижении единственного представителя коллектива в президиум собрания.Наказуемое превышение скорости автомобиля делится на диапазоны: до 10%, от 10% до 20%, свыше 20%. Однако если в регламентирующем документе заданы только диапазоны до 10% и от 10% до 100%, то это не будет соответствовать исчерпывающему множеству событий. Такие нестрогие определения возможного диапазона ситуаций являются причиной юридической казуистики, требующей дальнейшего исследования прецедента.
Итак, ИМС, которому соответствует множество высказываний А= {x1, …, xn}, характеризуется тем, что при соответствующих обстоятельствах одно и только одно высказывание из этого множества может принимать значение 1. Это и определяется операцией ИСКЛЮЧАЮЩЕЕ ИЛИ, которую будем обозначать
 |
 |
Очевидны главные свойства высказываний о событиях из ИМС:
 | (1.12) |
 | (1.13) |
Теорема. Логическая функция от переменных-высказываний о событиях, образующих исчерпывающее множество событий, преобразуется в дизъюнкцию ИСКЛЮЧАЮЩЕЕ ИЛИ переменных-высказываний о событиях из этого множества.
Доказательство. Для произвольной логической функции, заданной на исчерпывающем множестве высказываний {x1, …, xn}, СДНФ имеет вид

Рассмотрим первую конъюнкцию в СДНФ. Применив (1.12), (1.3) и (1.13), получим

Аналогично, вторая конъюнкция преобразуется

Третья конъюнкция содержит переменные с разными индексами, на что указывает не единственное вхождение единицы в выражение f(0, …, 1, 1). Эта конъюнкция имеет значение 0.
Таким образом, определяющее значение в СДНФ имеют лишь те конъюнкции, где в обозначении функции f указана единственная единица. Единичные значения f в таком случае определяют вхождение соответствующей переменной в результирующее выражение СДНФ.
Теорема доказана.
Чтобы подчеркнуть, что задание ситуаций подчиняется условию операции
 |
 |
 | (1.14) |
Каждая переменная, участвующая в формировании этого выражения, входит в него единственный раз.Единственность вхождения переменных достигнута на основе применения закона дистрибутивности с учетом свойств высказываний на исчерпывающем множестве событий.
Назовем преобразование логической функции, приведшее к единственности вхождения переменных, дистрибутивным.
Композиция исчерпывающих множеств
Для строгого логического мышления, исключающего неопределенность, приходится оперировать не отдельными событиями и даже не исчерпывающими множествами таких событий (высказываниями о них), а композициями таких множеств. Между событиями, принадлежащими различным множествам, возможна зависимость, порождающая сложные высказывания. Да и сами ИМС могут определяться и инициироваться обстоятельствами, обусловленными событиями из других ИМС. Связи между ИМС, образующие сложные высказывания, отображаются деревом логических возможностей.
Рассмотрим пример.
Пансионат для ветеранов труда обеспечивает постояльцам активный отдых круглый год. Представим схемой (рис. 1.1) распорядок дня отдыхающих. Такая схема и определит дерево логических возможностей.
Уровни ветвления могут формироваться разными способами. Например, первый уровень можно сформировать на основе времен года и т.д. Однако в порядке рекомендации можно следовать правилу "события располагаются на более низких уровнях по сравнению с теми уровнями, которые занимают события, от которых зависят данные события".
Бабушка пишет внуку: "Зимой я после завтрака катаюсь на лошади, и летом я после завтрака катаюсь на лошади, а также весной после завтрака прогулка бывает на лошади". …Что-то ей не нравится, и она строит схему своего составного высказывания: f = x1














Ответ следующий: необходимо на каждом пути в дереве логических возможностей, ведущем к заданному событию, построить конъюнкцию событий, образующих этот путь. Затем все такие конъюнкции объединить операцией дизъюнкции.
Поскольку используются только исчерпывающие множества событий, очевидно, что эта дизъюнкция выполняется с помощью операции
 |
 |

Полученная таким способом функция подвергается дистрибутивному преобразованию - "вынесению за скобки".
Отметим, что в результате такого способа построения искомая функция принимает вид, при котором каждая используемая переменная-высказывание входит не более одного раза.
Например, функция, отображающая такое событие в жизни бабушки, как езда на велосипеде, имеет вид


Рис. 1.1. Полное дерево логических возможностей
Однако далее будет показано, что не всегда единственного вхождения переменных можно добиться с помощью дистрибутивных преобразований. Иногда требуются дополнительные действия для его осуществления.
Определение 5. Совокупность всех исследуемых в данном контексте событий, т.е. множество - объединение всех рассматриваемых ИМС - образует факторное пространство событий.
Как и ранее, точку факторного пространства (ситуацию) будем обозначать {x1, …, xn}.
Итак, показана возможность построения логических функций на основе высказываний о событиях из факторного пространства.
Как видно из примера, факторное пространство событий отображается ветвящейся структурой на основе отдельных исчерпывающих множеств событий, входящих в его состав. Тогда подмножества, состоящие из таких ИМС, тоже являются факторными подпространствами, которые в некотором контексте можно исследовать отдельно.
Например, можно отдельно исследовать факторное подпространство, сформированное на основе первых двух уровней ветвления (рис. 1.2) в приведенном на рис. 1.1 дереве логических возможностей. Это может быть необходимо при планировании финансовых расходов пансионата на питание.

Рис. 1.2. Факторное подпространство для исследований финансовых затрат на питание
Можно, в соответствии с поставленной задачей (в контексте исследований), формировать другие факторные пространства событий.Например, планирование использования спортивного инвентаря по времени года приводит к целесообразности факторного пространства, структура которого показана на рис. 1.3.

Рис. 1.3. Факторное пространство для планирования использования спортивного инвентаря
Логические функции высказываний
Множество логических переменных - высказываний о событиях {x1, x2, …, xn} в контексте некоторого приложения образует пространство событий размерности n. Точка этого пространства является ситуацией.
Можно записать произвольную композицию на основе заданного множества переменных-высказываний и логических операций, например, ¬


(x



Высказывания (о событиях) в качестве переменных могут входить в состав сложных формирований - логических функций, принимающих (булевы) значения 1 (ИСТИНА) или 0 (ЛОЖЬ).
Определение 3. Имеющая смысл линейно-скобочная композиция операций ¬,


Таким образом, логическая функция является булевой функцией ситуаций.
В классической теории булевых функций [1] показывается, что каждая такая функция может быть представлена дизъюнктивной и (или) конъюнктивной нормальной формой. В первом случае ее структура выражается как дизъюнкция конъюнкций, во втором - как конъюнкция дизъюнкций.
Рассмотрим две логические функции
Y = x1



Z = (x1



Выражение Y представлено дизъюнктивной нормальной формой (ДНФ). Выражение Z соответствует конъюнктивной нормальной форме (КНФ), практически не применяемой.
Преобразуем
Z = (x1






Это - дизъюнктивная нормальная форма.
Практически, например, при конструировании электронных устройств, известно наперед, какой сигнал на отдельно взятом выходе должен формироваться при различных значениях сигналов на входе.
Тогда значения логической функции, описывающей формирование сигнала на данном выходе, задаются таблично, в зависимости от всех возможных ситуаций на входе. По такой таблице аналитическое выражение для искомой логической функции формируется в виде совершенной дизъюнктивной нормальной формы (СДНФ). Ее общий вид продемонстрируем на примере трех переменных:
 | (1.11) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |

После эквивалентных преобразований (начинающихся с вынесения x1 "за скобку") получим

Аналогично,

После эквивалентных преобразований находим

Из табл. 1.1 видно, что все значения Z и Z* от одних и тех же наборов значений переменных совпадают. Однако Z* образуется только двумя "слагаемыми" Z. Конъюнкция x1

В заключение этого раздела представим обобщение, построенное над СДНФ, - в соответствии с теоремой разложения, широко используемой при конструировании электронных схем на основе стандартного набора элементов. Как и ранее, продемонстрируем суть данной теоремы на примере четырех переменных:

Минимизация длины логической цепочки в системе принятия решений
Предваряя подробное исследование в последующих лекциях, отметим, что замена логических операций операцией суммирования при счете передаточной функции приводит к актуальности однократного учета всех входящих переменных, т.е. к единственности вхождения переменных в каждое логическое выражение, составляющее описание системы принятия решений. Выше с целью обеспечения такого единственного вхождения переменной был использован прием "размножения" решения R6.
При разработке электронных схем исследуется понятие "длина логической цепочки" - под ней подразумевается максимальное количество электронных элементов, которое должен преодолеть сигнал на входе схемы, пройдя последовательное тактируемое преобразование, чтобы на выходе схемы сформировался сигнал. От этой длины, определяющей время переходного процесса, зависит быстродействие схемы. Поэтому актуальной задачей является минимизация максимальной длины логической цепочки при возможности параллельного выполнения всех таких цепочек (что характерно для прохождения электрического сигнала по схеме).
Очевидно, что в схеме на рис. 1.4 максимальная длина логической цепочки равна двум.
Применим ко всем выражениям (1.17), каждое из которых является или может быть преобразовано в дизъюнкцию конъюнкций, прием "размножения" решений. Теперь (рис. 1.9) схема состоит из цепочек единичной длины. Каждый входной сигнал подвергается обработке только конъюнктором. Так как электронная схема полностью определяет конструкцию системы принятия решений на основе достоверности событий, то можно преобразовать полученную электронную схему в однослойную схему СПР, показанную на том же рисунке.

Рис. 1.9. Преобразование электронной схемы с единичной длиной логической цепочки в однослойную систему принятия решений
Таким образом, доказано следующее утверждение:
Лемма 1. Любая СПР, сформированная на основе логического описания булевыми функциями, способом "размножения" решений преобразуется в однослойную СПР на основе достоверности событий.
Преимуществом таких СПР является то, что они представляют собой таблицы с ассоциативной выборкой по принципу наибольшей похожести.
Конечно, можно за каждым решением закреплять один выход СПР, на котором объединить общее решение, полученное по разным путям, в виде текста. При корректно заданных исходных данных - на основе правил использования исчерпывающих множеств событий - СПР будет "работать" правильно, выдавая адекватные ответы. Тогда рекомендация "Прими решение R" будет выдана, а информация о пути, приведшему к этому решению, будет утрачена.
При составлении "электронной" схемы такое объединение производится с помощью операции дизъюнкции, что приводит к длине логической цепочки, равной двум. Но ведь если, формируя структуру СПР, строго следовать порядку построения "электронная схема

Таким образом, "размножение" решений - операция, свойственная СПР, что делает ее (СПР) построение отличающимся, развивающим "схемотехнический" подход. "Электронные" схемы целесообразно использовать на начальном этапе исследования логического описания СПР, а далее, оттолкнувшись от них, перейти к более совершенной однослойной структуре.
"Размножение" решений имеет важное достоинство. Оно позволяет установить причину, найти объяснение принимаемого решения. Это означает, что текст решения может быть дополнен указанием причины принятия именно такого решения.
Например, получив информацию о необходимости заказа велосипеда в отделе спортинвентаря, бабушка может воспользоваться и важным объяснением: "…потому что сейчас, скорее всего, весна, а вы, вероятно, только что сытно позавтракали" (рис. 1.10).

Рис. 1.10. Бабушка
В заключение данной лекции следует отметить, что построен алгоритм параллельных вычислений [6] сложных логических конструкций в области действительных переменных, предназначенный для реализации высокого быстродействия в системах управления и принятия решений.Более того, сведение СПР к однослойной приводит к применению лишь тех передаточных функций (элементов N1 на рис. 1.6 и рис. 1.9), которые имитируют конъюнкторы. Это служит повышению достоверности оценок, стандартизации и адекватности природным процессам.
"Схемотехническое" представление системы принятия решений
Отобразим (c нарушением некоторых стандартов) схемотехнически бабушкину СПР, подобно электронной схеме (рис. 1.4) с помощью конъюнкторов и дизъюнкторов. На вход будем подавать значения истинности переменных-высказываний (ситуации) так, чтобы на одном из выходов формировалась единица - значение истинности соответствующего решения. Задавать значение ситуаций следует корректно, чтобы соблюдать требования вхождения переменных в исчерпывающие множества событий.

Рис. 1.4. "Электронная" схема системы принятия решений
Реализовав эту схему на логических элементах, бабушка получит реальное средство подсказки: что она должна делать в данное время года и суток.
Например, бабушка хочет вспомнить, чем она должна заниматься летом после обеда. Она полагает x2 = x5 = 1 при нулевых значениях других переменных и запускает программу, моделирующую работу электронной схемы. На выходе R3формируется сигнал, соответствующий высказыванию "Верховая езда".
Электронная схема, имитирующая систему принятия решений, требует корректного задания исходной информации, т.е. корректной формулировки вопроса в соответствии со смыслом задачи. Одновременно должна существовать уверенность в получении единственного решения, в том числе предполагающего задание альтернативных вариантов, если это предусмотрено при построении СПР. В таком случае окончательный выбор альтернативы может быть предусмотрен при развитии системы, при анализе новых вводимых факторов. При некорректной формулировке вопроса возникнут коллизии, неоднозначные или неправильные выводы. Таким образом, СПР может отвечать только на те вопросы, на которые она настроена.
Система принятия решений
Для некоторой логической функции f от переменных из факторного пространства событий воспользуемся операцией следования (импликации) и сформируем логическое выражение вида
 |
(1.15) |
Здесь f следует рассматривать как выражение, определяющее условие, сложившуюся ситуацию, посылку, а R - высказывание, которое рассматривается как следствие: правило поведения, значение векторной функции, указание к действию и т.д. Таким образом, возможно формирование связей вида "посылка - следствие", "если …, то …". При этом функция f задается на множестве ситуаций и указывает на то, что, если на некоторой ситуации она принимает значение 1 (ИСТИНА), то такое же значение принимает высказывание R, являясь руководством к действию, к принятию определенного решения.
Подобно (1.16), можно описать множество логических выражений, определяющих стройную систему управления или принятия решений в соответствии со складывающейся ситуацией в факторном пространстве событий:
 |
(1.16) |
Определение 6. Система логических выражений вида (1.16), заданная на факторном пространстве (подпространстве) событий, обладающая полнотой и непротиворечивостью, называется системой принятия решений.
Поясним важность свойств, указанных в определении.
То, что система функций f1, …, fm является полной, означает, что любая точка факторного пространства событий входит в область задания хотя бы одной из этих функций. Непротиворечивость означает, что по каждой ситуации одна и только одна из этих функций принимает значение 1, приводящее к истинности соответствующего высказывания - решения. Однако отметим, что в действительности на основе смыслового содержания задачи по каждой или некоторой ситуации может быть известно более одного правильного решения, приводящего к успешным действиям. В таком случае высказывания об этих решениях могут быть объединены операцией ИЛИ, что приводит к приведенному выше предположению о непротиворечивости.
Продолжим рассмотрение примера.
Пусть известная нам бабушка планирует занятия физкультурой и спортом во все времена года по времени дня: после завтрака, после обеда и после ужина.
Объединяя высказывания по принципу "если …, то" и пользуясь обозначениями на рис. 1.1, она формирует систему принятия решений, которой, не полагаясь на память, намерена строго следовать, добившись согласия администрации.
Система имеет вид
 | (1.17) |

Однако выше не напрасно обращается внимание на целесообразность однократного вхождения переменных в подобное выражение (это будет изучено в лекциях 9 и 10). Выражение, полученное первоначально, с помощью дистрибутивных преобразований привести к такому виду не удается. Тогда бабушка решает разбить это выражение на два подобных, сформировав получение одного и того же решения на основе двух условий. Это и послужило появлению в (1.17) двух выражений, определяющих одно решение R6.
Легко убедиться, что все возможные ситуации факторного пространства событий охвачены, демонстрируя полную ясность действий бабушки.
Системы принятия решений могут образовывать сложные иерархические структуры. В этом случае необходимо, чтобы высказывания- решения R1, …, Rm отображали события, образующие ИМС.
Системы принятия решений на основе достоверности высказываний о событиях
Изменения, внесенные в дерево логических возможностей и представленные на рис. 1.5, отобразим в электронной схеме системы принятия решений, представленной на рис. 1.4. Теперь исходными данными (рис. 1.6) для конъюнкторов и дизъюнкторов, принимающих эти данные, становятся не булевы, а действительные значения, для которых логические операции не определены.

Рис. 1.6. Система принятия решений на основе достоверности событий
Следуя далее по пути приблизительных оценок (ибо практически достоверность, как категория теории вероятностей, принадлежит области весьма приблизительных оценок), разработаем некоторый суррогат операций конъюнкции N1 и дизъюнкции N2 на основе передаточной функции порогового элемента, преобразующего сумму входных величин в выходные значения, которые приближенно "напоминают" результаты упомянутых логических операций. Этот путь - путь ухода от точного выбора решения в сторону выбора решения на основе степени похожести ситуаций на уже известные, - путь ассоциативного мышления.
Существует множество вариантов подбора пороговой передаточной функции, лежащей в основе такого элемента.
Введем сквозную нумерацию всех узлов схемы, реализующих дизъюнкцию и конъюнкцию. Пусть i - номер такого узла, j - номер входа этого узла при количестве mi активных входов (в данном примере каждый узел имеет два входа), ?j - вес входа. Тогда простейшая передаточная функция fi, реализуемая i-м узлом для замены логических операций конъюнкции и дизъюнкции, имеет вид
 |
(1.18) |
Здесь fj - величина сигнала, поступающая на j-й вход.
Тогда элемент N1, подобный конъюнктору, может быть реализован при ?j = 1/mi, j =1, …, mi, с помощью существенно высокого порога (рис. 1.7), где значение


Рис. 1.7. Элемент N1
На этапе настройки и верификации СПР предполагается, что входные сигналы - булевы переменные, принимающие значения 0, 1.
Тогда целесообразно выбрать значение

При переходе к действительным переменным, когда вместо событий рассматриваются, например, лишь предполагаемые вероятности их наступления, экспериментальный выбор значения

Элемент N2, подобный дизъюнктору, реализуется, наоборот, при низком значении порога и при ?j = 1, j = 1, …, mi. Порог выбирается так, чтобы уже при возбуждении на одном входе возникал сигнал возбуждения на выходе. При этом сигнал на выходе не превышает "1" (рис. 1.8), а значение


Рис. 1.8. Элемент N2
Задав на входе СПР значения достоверности переменных-высказываний и рассчитав значения на выходах пороговых элементов, на выходах схемы получим некоторые значения. Максимальное из этих значений "голосует" в пользу соответствующего решения.
Предложения, касающиеся создания пороговых элементов N1 и N2, носят лишь рекомендательный характер. Здесь неограниченный простор для творчества.
Напомним, что корректность задания исходной информации (соблюдение условия нормировки на исчерпывающих множествах событий, оценки достоверности с помощью вероятностного дерева логических возможностей) гарантируют практически приемлемый результат. Если же на входах задавать что угодно, то СПР преобразует это в какую угодно рекомендацию по принципу "каков вопрос - таков и ответ".
На рассмотренном жизненном примере проанализируем принимаемые бабушкой решения на основе двух вариантов СПР: с помощью электронной схемы (рис. 1.4), использующей определенность знания о ситуации, и с помощью схемы, основанной на неопределенности, на предполагаемой достоверности этих знаний (рис. 1.6).
Кора
"Крошка сын к отцу пришел,
и спросила кроха:
- Что такое хорошо
и что такое плохо?"
В. Маяковский
Мы видим, что столь примитивная оптимизация целевой функции, принимающей только два значения - "хорошо" и "плохо", может быть использована лишь на начальной стадии изучения и применения принципов нейросети. Можно построить занимательную игрушку (как весь наш мир!), веселый аттракцион…
Очевидно, что мы не можем оставаться на том примитивном уровне, когда по предъявляемому изображению мы получаем заключение типа "это буква х", "это - хорошо (вкусно)", "это - плохо" и т.д. В научном приложении на таких принципах можно построить модель собачки Павлова, демонстрирующую условный рефлекс при предъявлении этикетки "Pedigrее".
Но более серьезные применения должны использовать более сложные критерии логической выводимости. Ведь хронология Божественных событий Сотворения Мира закончилась созданием Человека!.. И тут начались проблемы… Эти проблемы обусловлены вопросом, запретным плодом райского сада: "Ну, и что же из этого следует?"
Цепочки логических выводов, производимые человеком, содержат не одно, а много звеньев. Сделанные выводы вновь входят в конфигурацию изображений (входных векторов) для новых выводов, действий и т.д.
Буква нужна, чтобы распознать слово. Слово - чтобы распознать предложение, уяснить его смысл, предпринять адекватные действия и т.д. (вспомним исходную посылку Иоанна Евангелиста: "В начале было Слово").
Тогда возникает вопрос о целесообразной структуре сети, где одни выводы, собираясь в различные конфигурации, как бы множась, вновь участвуют в формировании новых выводов. Здесь можно предположить как прямые, так и обратные связи, когда попутно сделанные выводы уточняют правильность всего умозаключения.
Технически возникает вопрос о такой концентрации выводов, когда совмещены понятия входного и выходного слоев. Это наводит на мысль о целесообразности существования такого универсального слоя - коры со связями между отдельными нейронами и целыми областями. На коре концентрируются выводы для немедленного участия в формировании других выводов.
По-видимому, таков ход мыслей Господа Бога, создавшего кору головного мозга не подумав о греховных последствиях. Так чисто технически можно доказать ее целесообразность.
Модель мозга
Нейросеть содержит узлы - аналоги нервных клеток - нейронов (рис. 2.7) (нейроподобных элементов, НПЭ) и их соединения - синапсические связи.

Рис. 2.7. Нейрон
Модель нейрона во взаимодействии с другими нейронами нейросети представлена на рис. 2.8.

Рис. 2.8. Модель нейрона
Здесь Vki
- энергетические доли импульсов Vk
, выработанных другими нейронами и поступивших на дендриты нейрона i, ?ik
- веса дендритов, hi
- пороги. В свою очередь, выработанный импульс Vi
также распределяется между дендритами нейронов, с которыми связан нейрон i с помощью ветвящегося аксона. В соответствии с законом распределения энергии, величина Vi
делится пропорционально значениям весов дендритов "принимающих" нейронов.
Впрочем, проблему деления (или неделения), лежащую в основе практических моделей, мы еще обсудим далее.
Каждый нейрон или управляем извне, или сети строятся по принципу самоуправления, используя обратные связи. А именно, можно регулировать значения весов синапсических связей {?i} и значения порогов hi
. Такое регулирование, во многих вариантах реализованное в разных моделях, и определяет возможность обучения и самообучения сети. Оно задает пути прохождения возбуждений через сеть, простейшим образом формируя связи "посылка - следствие".
На рис. 2.9 дается фрагмент нейросети, по которому мы можем представить следующее.

увеличить изображение
Рис. 2.9. Нейронная сеть с "правдоподобным" распределением сигнала возбуждения
Функции f бывают различны, но просты по объему вычислений. В простейшем случае f cовпадает с линейной формой - указанным аргументом. Т.е. по всем дендритам с учетом их весов (на рис. 2.9) производится суммирование и сравнение с порогом "

\begin{array}{l} V_i = \xi (( \omega_{i1}V_2+\omega_{i2}V_4) -h),\\ \xi (x) = \left \{ \begin{array}{ll} 0, & \mbox{при } x < 0 \\ x, & \mbox{при } x \ge 0 \end{array} \right \end{array} " width="227" height="67">
Величина превышения порога является величиной возбуждения нейрона или определяет значение величины возбуждения (например, в некоторых моделях величина возбуждения всегда равна единице, а отсутствие возбуждения соответствует нулю).
В некоторых моделях допускают и отрицательную величину возбуждения. Значение возбуждения передается через ветвящийся аксон в соответствии со связями данного нейрона с другими нейронами.
В общем случае по дендритам может передаваться как возбуждающее, так и тормозящее воздействие. Первое может соответствовать положительному значению веса синапсической связи, второе - отрицательному. Аналогичный эффект достигается при передаче отрицательных значений возбуждения нейронов.
В сети распознают входной (рецепторный) слой, воспринимающий внешние возбуждения (например, на который подается видеоизображение), и выходной слой, определяющий результат решения задачи. Работа сети тактируется для имитации прохождения по ней возбуждения и управления им.
Существуют два режима работы сети: режим обучения и режим распознавания (рабочий режим).
Установим случайным образом начальные значения весов дендритов всей сети. Пусть нейросеть предназначена для распознавания рукописного текста. Тогда входной слой аналогичен сетчатке глаза, на который ложится изображение. Его подача на входной слой возбуждает в некоторой конфигурации множество нейронов-рецепторов. Пусть мы на входной слой подали и поддерживаем некоторый эталон, например букву А. Через некоторое время возбудится (максимально) нейрон выходного слоя, который мы можем отметить как образ А (прохождение возбуждения отмечено темным цветом). Т.е. его возбужденное состояние мы воспринимаем как ответ "Это буква А". Введем снова букву А, но с естественными искажениями, обусловленными почерком, дрожанием руки и т.д. Может возбудиться тот же нейрон, но может и другой. Мы же хотим "научить" систему, заставить ее ответить, что это - тоже буква А, т.е. добиться возбуждения того же нейрона выходного слоя.
Тогда по некоторому алгоритму (один из известных алгоритмов называется алгоритм обратного распространения ошибки; в нем воспроизводится подход, используемый в динамическом программировании, здесь мы предлагаем алгоритм "трассировки") мы меняем веса и, возможно, пороги в сети на пути прохождения возбуждения так, чтобы заставить возбудиться нужный нейрон.
Таким способом, предъявляя множество эталонов и регулируя параметры, мы производим обучение сети данному образу. (Математические проблемы несовместимости управления параметрами для разных эталонов оставим в стороне: в живой природе такой процесс проходит успешно, достаточно устойчиво при разумном отличии эталонов. Например, интуитивно ясно, что пытаться заставить один и тот же нейрон выходного слоя возбуждаться и на строчную, и на прописную букву А вряд ли разумно. В лучшем случае он определит, что это буква вообще, а не, скажем, знак пунктуации.)
Обучение заканчивается тогда, когда вероятность "узнавания" достигнет требуемого значения, т.е. необходимость корректировки параметров по предъявляемым эталонам возникает все реже. Теперь можно работать в режиме распознавания - в том ответственном режиме, для которого сеть создавалась. Предъявляем сети различные буквы. Можем быть уверены, что с большой вероятностью, если мы предъявим случайно искаженную и даже зашумленную букву А (конечно, в допустимых пределах), сеть ее распознает, т.е. максимально возбудится соответствующий нейрон выходного слоя.
Можно существенно облегчить обучение, предъявляя эталон "в полном смысле", т.е., например, показывая букву, точно регламентируемую букварем. Тогда предусмотренная (!) степень отклонения от этого эталона, обусловленная почерком, будет влиять на вероятность распознавания этой буквы. Далее мы будем рассчитывать именно на такой способ обучения.
Теперь обобщим "специализацию" входного слоя, связав его с некоторыми характеристиками исходной ситуации (входного вектора), по которой необходимо принимать решение - формировать выходной вектор. Мы учим сеть по эталонным ситуациям, по которым мы знаем решение, а затем в рабочем режиме она выдает нам решение во всем диапазоне ситуаций. При этом она автоматически решает проблему, на какую "знакомую" ей ситуацию более всего похожа введенная ситуация, и, следовательно, какое решение следует выдать. Конечно, с определенной вероятностью правильности.
Такая обработка входной информации при возможном применении в сфере развлечений показана на рис. 2.10 и рис. 2.11.
Отметим, что в экспертных системах требуются точные данные о ситуации, чтобы выдать соответствующее ей заключение. Нейронной сети такой подход "чужд". Она выдает ответ на вопрос "На что похожа данная ситуация?" и, следовательно, какое должно быть заключение. Это еще раз подтверждает, что нейросеть имитирует ассоциативное мышление.

увеличить изображение
Рис. 2.10. Реакция на угрозу

Рис. 2.11. Реакция на поощрение
Обучение нейросети
Теперь предположим, что структура сети (рис. 2.5), а также передаточная функция (та же), заданы, и нам предстоит обучить сеть распознаванию букв О и А.

Рис. 2.5. Нейросеть, подлежащая обучению
Пусть экран разбит на столько же клеток, и мы убеждаемся лишь в том, что предложенная нейросеть содержит не менее 12 нейронов входного слоя, а также не менее двух нейронов выходного слоя.
Теперь возникла необходимость отразить истинный характер преобразования нейроном входной информации, т.е. величин возбуждения нейронов, связанных с ним. Дело в том, что все входы нейронов обладают регулируемыми (!) весами (синапсическими весами, весами связей), позволяющими направлять прохождение возбуждения в сети. С помощью этого регулирования можно связывать конфигурации и возбуждения нейронов входного слоя (посылка) с максимальным возбуждением определенных нейронов выходного слоя (следствие), формируя связи "если …, то …".
В связи с этим передаточная функция нейрона, в частности заданная нам или выбранная нами сознательно, имеет общий вид

Здесь ?j
- синапсический вес входа или вес связи, по которой передается возбуждение от нейрона j нейрону i.
Тогда задачей обучения является выбор высоких весов некоторых связей и малых весов других связей так, чтобы в соответствии с функциональным назначением сети сложились отношения "посылка - следствие", подобные тем, которые мы создали выше при построении уже обученной сети. Они переводят возбуждение рецепторов, образующееся при "показе" эталонов и образов, в максимальное возбуждение тех нейронов выходного слоя, которые говорят, "что это такое".

Рис. 2.6. Обученная нейросеть
Для простоты положим максимальный вес связи единичным, а минимальный оставим нулевым. Это соответствует тому, что, интерпретируя связи в сети как "проводочки", мы какие-то из них оставим (считая их сопротивление нулевым), а другие, ненужные, "перекусим".
Изложенная идея обучения по четко заданным эталонам воплощена в алгоритме трассировки нейросети.
На рис. 2.6 приведен результат такой трассировки для нашего примера, где выделенные стрелки соответствуют связям с единичными весами, а другие - с нулевыми.
Просчитав несколько, в том числе "неопределенных", образов на входе, можно убедиться в ее правильной работе, хотя и демонстрирующей изначально выбранное слабое отличие О от А.
Получилась интересная игра. Мы задаем на входе случайные возбуждения и спрашиваем: на что это больше похоже из того, что "знает" нейросеть? Все, что надо сделать, это посчитать в едином цикле для каждого нейрона значение передаточной функции и проанализировать величины возбуждения нейронов выходного слоя.
Построение обученной нейросети
Пусть перед нами экран, разбитый на двенадцать клеток, 4?3. Клетки отображают дискретность элементов изображения. При фокусировании изображения клетка либо засвечивается, либо нет. "Засветка" определяет единичное значение величины ее возбуждения, "не засветка" - нулевое. Так, буква О
определяет засветку клеток, определяемую на рис. 2.1. Буква А засвечивает экран, как показано на рис. 2.2.

Рис. 2.1. Обучение букве "О"

Рис. 2.2. Обучение букве "А"
Что надо сделать для распознавания этих двух букв? Для того, чтобы некий конструируемый нами прибор мог сказать, какая это буква?
Очевидно, надо все сигналы возбуждения клеток экрана, засвечиваемой буквой О, подать на конъюнктор, реализующий схему И. Единичный сигнал на выходе конъюнктора, как показано на рис. 2.1, сформируется тогда и только тогда, когда засветятся все клетки экрана, на которое ложится изображение буквы О. Наличие единичного сигнала на выходе конъюнктора и определит ответ "Это буква О".
То же необходимо сделать и для буквы А.
Пометим каждую клетку экрана ее координатами. Тогда на языке математической логики сделанное нами можно записать в виде логических высказываний - предикатов:
(1,2)






(1,2)








Эти предикаты определяют "электронное" воплощение методами схемотехники.
При этом буквы не будут "мешать" друг другу, так как засветка соответствующих им клеток экрана частично не совпадает и единичное значение конъюнкции определится только для одной из них.
А если на экран подать букву К? Тогда ни один из двух конъюнкторов не выработает единичное значение, так как не произойдет полное совпадение засветки соответствующих им клеток экрана. Чтобы "научить" систему букве К, необходимо ввести еще один конъюнктор и проделать те же построения, что и выше.
Таким образом, мы можем говорить, что построили систему распознавания двух "правильно" заданных букв.
Но что делать, если буквы на экране пишутся дрожащей рукой? Тогда мы должны разрешить альтернативную засветку каких-то соседних клеток экрана и учитывать это с помощью операции дизъюнкции, ИЛИ. Как известно, в результате выполнения этой операции формируется единичный сигнал в том случае, если на входе есть хоть один единичный сигнал.
Рассмотрим возможность распознавания буквы О, допустив возможность засветки клеток (1,1), (1,3), (4,1), (4,3). Тогда ранее построенный предикат примет вид
((1,1)










Аналогично, для буквы А допустим засветку клеток (1,1) и (1,3):
((1,1)










Объединив оба предиката, получим схему на рис. 2.3.
Таким образом, мы реализовали для обучения и распознавания "схемотехнический" подход, основанный на применении булевых функций и оперирующий булевыми переменными 0, 1.
Теперь совершим тот шаг, тот переход, который и определяет гениальную простоту природного воплощения, рассчитанного на неполноту данных, недостоверность, "зашумленность", высокое быстродействие, надежность и унифицированность. Ибо мы не можем представить себе электронную схему, укрытую в черепной коробке.

Рис. 2.3. Совместное обучение буквам "О" и "А"
Природа (и мы, как ее часть) никогда не располагает точной, определенной и достоверной информацией. Засветка клеток экрана, как и рецепторов нашего глаза, не бывает полной, образ не бывает правильным, присутствуют шумы, пропуски и т.д. Тогда жизненную важность обретают понятия похожести, ассоциаций. "На что более всего похож "показанный" образ, возникшая ситуация, и какие ответные действия наиболее обоснованы?" - вот вопрос, определяющий принцип нашей жизни среди многих опасностей и свершений. Ассоциативность нашего мышления является абсолютной.
Значит, надо уйти от вполне определенных булевых переменных (0, 1, "да - нет", "белое - черное" и т.д.) в сторону неопределенности, достоверности или других оценок информации, - в сторону действительных переменных.
Но тогда необходимо уйти и от булевой алгебры, так как понятия конъюнкции и дизъюнкции для действительных переменных не определены.
Тут и приходит на помощь анализ и применение принципов природной реализации - принципов нейронной сети, воплощенных в нашем мозге.
Преобразуем полученную нами обученную схему в нейронную сеть (рис. 2.4).
Каждая клетка экрана - это нейрон-рецептор, который в результате засветки обретает некоторую величину возбуждения, принимающую значение между нулем и единицей. Рецепторы, заменившие экран, образуют входной, или рецепторный, слой нейросети. Каждый конъюнктор и дизъюнктор заменим единой для всей сети моделью нейрона. Введем выходной слой сети, состоящий в нашем примере из двух нейронов, возбуждение которых определяет результат распознавания. Назовем нейроны выходного слоя по названиям букв - О и А.
Рецепторы, подобно экрану, возбуждаются извне. Все же другие нейроны, имитируя распространение возбуждения в мозге, реализуют передаточную функцию. Она преобразует сигналы на входе нейрона, с учетом весов этих входов (пока отложим их рассмотрение), в величину возбуждения данного нейрона, передаваемого далее по сети в соответствии со связями нейронов и достигающего выходного слоя.
Поскольку работа мозга имитируется на логическом уровне, передаточная функция выбирается достаточно простой. Так, в нашем примере достаточно выбрать следующую передаточную функцию для нахождения величины возбуждения i-го нейрона:


Рис. 2.4. Нейронная сеть для распознавания букв "О" и "А"
Здесь суммируются все сигналы (величины возбуждения), которые пришли от нейронов, связанных с данным. Порог может быть единым для всех нейронов.
Проверим, как построенная нейросеть реагирует на четко заданные эталоны букв. Под четкостью будем понимать то, что величина возбуждения, реально отражающая достоверность, максимальна и равна единице. Пусть при показе буквы О засветились нейроны-рецепторы (1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 3), (4, 2).
Тогда, при h = 0 величины возбуждения нейронов примут значения V1 = 3 , V2 = 1 , VO = 8 , VA = 7 . Нейрон О
возбудился более, чем нейрон А, указывая тем самым, что скорее всего была показана буква О. Аналогично можно рассчитать реакцию нейросети на все возможные конфигурации четко заданных эталонов букв.
А теперь введем ту самую неопределенность, к которой мы так стремились. Пусть в процессе показа буквы О четкость утрачена и величины возбуждения нейронов-рецепторов принимают значения V(1,1) = 0,2 , V(1,2) = 0,7 , V(1,3) = 0 , V(2,1)
= 0,5 , V(2,2) =0,1 , V(2,3) = 0,5 , V(3,1) = 0,5 , V(3,2) = 0,5 , V(3,3) = 0,1 , V(4,1) = 0,4 , V(4,2) = 0,4 , V(4,3) = 0,5 . Считаем: V1
= 0,9 , V2 = 1,3 , VO = 3,8 , VA = 3,9 .
Что ж, по-видимому, мы потребовали невозможного. Ведь при таком "крупнозернистом" экране налагаемые на него образы букв О и А пересекаются весьма существенно, и зашумленный показ букв обладает малой устойчивостью.
Рассмотренный принцип распознавания является обобщением принципа простейшего Персептрона, предложенного Ф. Розенблатом в 1959 г. [4] и ставшего классическим.
Пространство признаков
Выше неявно проявилась лишь следующая модель. Образ буквы, например а, налагается на входной слой нейросети - рецепторы. Конфигурация возбужденных рецепторов, порождая прохождение возбуждения через внутренние слои нейросети (образуя путь возбуждения), определяла возбуждение (если не гасло по пути) одного из нейронов выходного слоя, говорящего "это буква а". Интуитивно ясно, что устойчивость такой схемы по отношению к огромному множеству конфигураций возбуждений рецепторов, соответствующих одной только букве а, вряд ли высока. Вглядываясь в себя, мы видим, что такое непосредственное распознавание осуществляется далеко не всегда, особенно на этапе получения школьного образования, ибо наше образование получается на основе признаков и определений (правил вывода).
Как мы характеризуем строчную букву а? Это кружочек, справа примыкает палочка с хвостиком вправо.
А прописная А? Две палочки с перекладинкой. Но ведь буква Н тоже соответствует этому определению. Тогда мы добавляем: две палочки, соединенные вверху. (Кстати, соединение вверху может быть в результате небрежности лишь обозначено. Тогда о намеке на него мы можем судить по наклону палочек. Дальнейшая небрежность может привести к неразличимости букв А и Н.)
Значит, существует ряд признаков, лежащих в основе определений. И мы на интуитивном уровне понимаем, что такой способ распознавания гораздо более устойчив к искажениям и особенностям почерка, однозначен и надежен. Ведь при изображении буквы А можно допустить не только небрежность в верхнем соединении палочек, но и значительную разницу в общем наклоне буквы, в длинах боковых палочек, в месте расположения перекладины, в ее наклоне и длине и т.д. Искажение может привести к сомнениям лишь при крайней похожести на цифру 4, на телеграфный столб или на греческую ?. Но даже в этом случае окончательный вывод может быть сделан на основе контекста, т.е. по использованию дополнительных признаков "по умолчанию".
Значит, в нашем случае необходимо ввести такие признаки, как наличие кружка, палочек, хвостиков, их взаимного расположения и т.д.
То есть необходимо построить пространство признаков , преобразовать наши входные изображения в это пространство, и тогда появится возможность получения более определенного и устойчивого к искажениям заключения.
Перевод входного изображения в пространство признаков значительно расширяет возможности "разглядывания" - масштабирования, размещения, поиска угла наклона и т.д., т.е. позволяет с более высокой достоверностью производить распознавание.
Например, изображение танка может в разных ракурсах ложиться на входной слой рецепторов. Конечно, можно запомнить, что "и это - танк", "и это - тоже танк" и т.д. Но если ввести хотя бы такое определение, достаточное для соседки - тети Маши, как "массивный корпус на гусеничном ходу (тоже нуждается в определении!), а сверху башня с дулом пушки, и все такое зелененькое", то это научит хотя бы принимать меры предосторожности.
Устойчивость, помехозащищенность и локализация максимального возбуждения
"…Цинциннат брал себя в руки и, прижав к груди, относил в безопасное место".
В. Набоков. "Приглашение на казнь"
На рассмотренном маленьком примере, где мы предположили жесткое закрепление нейронов выходного слоя между образами, принцип ассоциации "на что более всего это похоже" пока не виден. Как же он появляется?
Уместны ассоциации, предположения о том, как это реализовано в природе.
Представим себе отдельно выходной слой (рис. 2.17).

Рис. 2.17. Области возбуждения
Рассматривая прохождение возбуждения, например, при подаче того же изображения буквы А, в модели нейросети, ближе к реальному мы можем предположить, что не один нейрон, строго соответствующий этой букве, придет в возбужденное состояние, как это предполагается в логической модели, в его окрестности возбудятся и другие нейроны. Эта величина возбуждения будет угасать с ростом удаления. Нам же будет нужно, чтобы максимальной величиной возбуждения в этой окрестности обладал именно отмеченный нейрон. Более того, желательно, чтобы этот и только этот нейрон обладал высокой, существенно различимой величиной возбуждения. Это обеспечит определенность и однозначность при дальнейшем использовании полученного вывода для принятия решения и для построения других логических цепочек, использующих это решение. Такая локализация сигнала возбуждения позволяет ответить на вопрос: "на что более всего похож предъявляемый образ, несмотря на случайные отличия и оказываемые помехи?"
Кстати, такое предположение указывает на другое, фактически реализуемое предположение о непрерывности перерастания свойства похожести одних образов в другие. Следование этому принципу при принудительном закреплении нейронов выходного слоя способствует построению адекватных моделей. А точнее, подавая первый раз букву А, не следует указывать системе, какой нейрон выходного слоя должен возбудиться. Лучше подать достаточно "правильный" эталон и посмотреть, какой нейрон возбудится. Этот нейрон и будет впредь соответствовать нашей букве.
Возбуждения именно этого нейрона мы будем добиваться при предъявлении других эталонов.
(Хотя, мы же далее предполагаем, на основе уже рассмотренных примеров, что первоначально сеть "пуста", т.е. все веса - нулевые. Путь же возбуждения прокладывается, "трассируется".)
Способы максимизации и локализации уровня возбуждения основаны на нахождении экстремума функции возбуждения, построенной на области выходного слоя. Здесь нельзя обойтись без обмена тормозящими воздействиями между нейронами выходного слоя. Простейшая идея состоит в следующем. Все нейроны области выходного слоя имеют между собой синапсические связи, так что каждый нейрон связан с ближайшими нейронами тормозящими связями, по модулю пропорциональными величине собственного возбуждения. Тогда в итоге взаимодействия двух нейронов (один из алгоритмов такого взаимодействия нейронов выходного слоя будет рассмотрен) более "сильный" нейрон сохранит положительный (хотя и меньший) потенциал, сообщив более "слабому" нейрону тормозящее воздействие. Такое пошаговое "голосование" на фоне приходящего подтверждения от эталона и выделит сильнейшего.
Итак, мы видим, что обучение сети неразрывно связано с локализацией возбуждения на выходном слое.
Анализируя все сказанное выше, мы можем попытаться собрать некоторую универсальную модель нейросети. В ней будут присутствовать входной и выходной слои. Картина возбуждений выходного слоя при подаче изображения на входной слой будет представлять собой (после аппроксимации в непрерывную область определения из дискретной) непрерывную функцию, максимум которой должен определить нам необходимое заключение. Однако на этапе обучения (да и в рабочем режиме - с удовлетворяющей нас достаточно малой вероятностью) по ряду предъявляемых эталонов этот максимум не совпадает с желаемым ответом. Следовательно, путь распространения возбуждений внутри сети необходимо скорректировать изменением синапсических весов нейронов, оказавшихся задействованными в этом процессе.
Было сказано, что предварительная локализация максимума величины сигнала производится в результате взаимодействия нейронов в области или некоторой окрестности выходного слоя или коры. Получается так, что области возбуждений оказываются "закрепленными" за типами объектов - за буквами, цифрами, продуктами питания и т.д. В развитой сети, где становится актуальным понятие коры, нейроны отдельных ее областей через нейроны внутренних слоев вновь порождают пути прохождения возбуждений в другие области коры и т.д.
Пытаясь разгадать и воспроизвести универсальную нейросеть, мы вновь и вновь пытаемся "заглянуть в зеркало". Мы видим, что хотя отдельный нейрон обладает возможностями взаимодействия с огромным числом нейронов (нейрон имеет до 10 тысяч дендритов), это взаимодействие характеризуется локальностью. А именно, несмотря на случайность связей, вероятность связи с "близким" нейроном значительно выше вероятности связи с нейроном "далеким". Об этом говорят даже исследованные длины дендритов и аксонов. (Длина дендрита достигает одного миллиметра; однако длина аксона достигает сотен миллиметров. При этом применяется, по-видимому, усредненная характеристика, вряд ли принимающая во внимание нейроны только лишь головного мозга.)
Такой принцип локальности, пронизывающий всю структуру сети, в сочетании с принципом иерархии - возможностью построения новых выводов на основе сделанных - позволяет на деле реализовать связи "каждый с каждым". Никакой вывод не может оставаться недоступным и неиспользованным при построении сложных умозаключений.
Принцип локальности обеспечивает минимизацию входной информации, существенное влияние лишь значимых признаков на заключение, контролируемое и диагностируемое по функциональное разбиение областей нейросети, определение и выделение той области нейросети, в синапсические веса которой необходимо внести поправки в процессе обучения (например, организовать прилив крови).
Принцип локальности не отвергает существования маловероятных связей "каждый с каждым".
Эта вероятность может быть высокой вследствие аномалий генетического характера. Например, человек, которого мы относим к уникумам, может видеть кожей вследствие того, что нейроны, воспринимающие кожные ощущения, сильно связаны с нейронами выходного слоя, "отвечающими" за зрение. И вместо того чтобы возбуждение в сторону последних при слабых связях угасло, оно становится результативным. Ведь в целом все нейроны устроены одинаково!
Большое число связей способствует высокой надежности мозга. Ведь ежедневная гибель огромного числа нейронов, подхлестанная алкоголем и наркотиками, а также травмы, компенсируются другими путями прохождения возбуждений, иногда даже связанными с необходимостью переобучения. Впрочем, ограниченный ресурс возможного не спасает, в конце концов, от деградации.
Итак, рассмотрим более подробно процесс локализации максимальной величины возбуждения на выходном слое, заключающейся в выделении того нейрона некоторой малой области, величина возбуждения которого максимальна. Он основан на подавлении тех сигналов возбуждения нейронов, которые не соответствуют нейрону с максимальным возбуждением. Т.е. если необходимо сконцентрировать сигнал и выделить нейрон с максимальной величиной возбуждения, это достигается с помощью подавляющих связей, с которыми действуют друг на друга "соседние" нейроны выходного слоя.
Пусть в целом над нейронами выходного слоя, условно расположенного на плоскости (x, y), можно построить непрерывную функцию их возбуждения P(x, y) (рис. 2.18), обусловленную прохождением сигналов возбуждений в сети на основе предъявленного эталона. Будем считать, что эта функция имеет один или более максимумов. Пусть Pij
- значение величины возбуждения нейрона с координатами (i, j).
Каждый нейрон (i, j), действуя в своей окрестности, рассылает соседним нейронам, на их дендриты с отрицательными, не обязательно регулируемыми, весами, свою величину возбуждения Pij, первоначально полученную из сети.
Представим взаимодействие двух "близких" нейронов, например (i, j) и (i, j+1), получивших первоначально разные значения величин возбуждения из сети.
Пусть Pij > Pi,j+1
. Тогда в очередном такте времени на входе нейрона (i, j) появится подавляющий сигнал Pi,j+1
, а на входе нейрона (i, j+1), и так имеющего меньшее значение величины возбуждения, - подавляющий, больший сигнал Pij
.

Рис. 2.18. Проблема локализации возбуждения
При подтверждаемом на входном слое эталоне, т.е. при существовании на некотором отрезке времени характера и величины возбуждений, обусловливающих возбуждение выходного слоя, на выходном слое, в частности между нейронами (i, j) и (i, j+1) , происходит перераспределение величины возбуждения.
А именно: несомненно, уменьшится значение Pij
, но в еще большей степени уменьшится значение Pi,j+1
. В следующем такте более "сильный" нейрон еще более "ослабит" более "слабый" нейрон, который, в свою очередь, сможет еще в меньшей степени "ослабить" более "сильный" нейрон и т.д. Более того, "слабый" нейрон может "слабеть" до тех пор, пока взвешенная сумма подаваемых ему сигналов не станет меньше его порога.

Рис. 2.19. Локализация возбуждения
Рассматривая этот процесс в рамках взаимодействия всех нейронов области выходного слоя, можно сделать вывод о постепенной концентрации высокого уровня возбуждения, присущего одному или нескольким нейронам и определяющего один или несколько локальных максимумов.
При таком взаимодействии нейронов области возбуждения выходного слоя происходит лишь усиление сигнала наиболее возбужденного нейрона. Полное подавление возможно лишь на границе этой области. Если где-то внутри области возбуждение некоторого нейрона окажется подавленным полностью (сигнал не преодолевает порога), то в следующем такте этот нейрон не сможет подавить сигнал того нейрона, который до того имел более слабый сигнал возбуждения. Тогда возможно появление в такой области возбуждения нового локального максимума. Таким образом, веса отрицательных связей должны способствовать максимальному усилению возбуждения того нейрона, который первоначально продемонстрировал максимальное возбуждение, при затухании возбуждения нейронов в сторону периферии.
На человеческом языке это означает: "Любое угадывание не исключает сомнений".
Однако всегда ли необходимо на выходном слое локализовать величину возбуждения?
По-видимому, такое усиление уровня возбуждения необходимо для того, чтобы единственный нейрон выходного слоя преодолел некоторую "планку" (изменяющуюся?), чтобы объявить себя ответственным за сделанный вывод или решение.
Однако следует отметить, что локализация и максимизация возбуждения на выходном слое особенно важны тогда, когда действительно необходима высокая степень определенности. Это важно в том случае, если получаемый вывод (решение) немедленно участвует в цепочке последующих, использующих его выводов.

Рис. 2.20. Нейродегустатор
В конце концов, все обусловлено назначением сети, решаемой задачей. Можно представить себе возможный аттракцион - реакцию фантастического чудовища на изображение, как это представлено на
рис. 2.10 и рис. 2.11. По виду изображения инициируются те или иные программы действий: радости, гнева, поднятия лап, виляния хвостом и т.д. Возбуждение определенных нейронов выходного слоя связывается с запуском соответствующих программ. Величина возбуждения может являться основным параметром для этих программ. Программы не исключают друг друга, и в одном такте могут запускаться несколько программ.
Можно представить радостную модель гурмана-дегустатора (рис. 2.20), по аромату блюда определяющего состав использованных ингредиентов и приходящего в восторг или в уныние от представленного букета.
В большинстве частных задач, где нейросеть обучается с помощью "учителя", т.е. на основе действий извне при ее настройке, присутствует элемент принудительного закрепления нейронов выходного слоя за выводами. В процессе последующего обучения преимущественно с помощью весов синапсических связей добиваются адекватной реакции сети.
Ввод и "разглядывание" эталонов и образов
Устройства ввода информации - эталонов, входных векторов, исходных ситуаций - имеют определяющее значение для нейросети. С их помощью формируются и поддерживаются возбуждения входного слоя. Однако связь модели живого организма с внешней средой естественно представляет собой сложную проблему - конгломерат ряда частных технических и алгоритмических проблем. Среди них - успешно решаемая проблема видеоввода. Однако ввести в компьютер "картинку" - это лишь часть дела. Картинку надо обработать - в целом и по частям, чтобы по максимуму интересующей информации получить полные и достоверные выводы. Здесь мы ищем аналоги нашего восприятия действительности.
Мы совершаем обзор представляемой нам картины тремя способами:
сканированием сектора обзора, разбитого на элементарные сегменты (рис. 2.12);
сканированием сектора обзора со "своим окном просмотра" (рис. 2.13);
спонтанным обзором, обусловленным привлечением внимания к цветовому или скоростному всплеску, быстрым увеличением размера (угрожающим приближением) объекта, указанием извне (целеуказанием) и т.д. (рис. 2.14).
Третий способ также требует сканирования сектора обзора, однако со значительно меньшими энергетическими затратами.
При первом и втором способах анализ сложнее, т.к. требует согласования всего виденного по сегментам. Это, в свою очередь, требует включения высших уровней логического вывода (интеллекта).
При третьем же способе можно добиться избирательности, чрезвычайности реакции, например на резкие движения, на бег, появление яркой расцветки в одежде и т.д. Это может с успехом использоваться в развлекательных, игровых системах.
Все способы реализуются легче, если речь идет о единственном объекте единовременного распознавания, например буквы, хозяина квартиры, подписи и т.д. Ибо любая сцена, например туристская группа, пришедшая полюбоваться "умным" монстром, требует не только детального, но и совместного анализа этим монстром всех (многих) ее составляющих.

Рис. 2.12. Сканирование по строкам

Рис. 2.13. Реакция на внезапность

Рис. 2.14. Беспорядочное сканирование
Впрочем, говоря о туристах, можно говорить о конечной, усредненной реакции на всю группу. Ведя обзор, сеть постепенно, по критериям обучения "это хорошо - это плохо", воспринимая "настроение" как последовательное добавление элементов радости и огорчения, приходит к некоторому окончательному состоянию, обусловленному тем, сколько того и другого она увидела. Тогда для разных групп туристов или экскурсантов это состояние будет разным. Это может стать источником веселья и шутливого "поощрения" той группы, которая привела объект в радость, и "осуждение" группы, ввергнувшей его в печаль.
Итак, в каждом такте обзора, формируется сегмент, содержимое которого необходимо распознать. Чаще всего целесообразно допущение о том, что в элементарном сегменте (или в "окне просмотра") при дискретном сканировании находится не более чем один значимый объект. Пусть это - максимальная область текста, вмещающая единственную букву, написанную с допустимой долей небрежности. Как помочь себе же разглядеть эту букву? По-видимому, следует пытаться разместить эту букву на входном слое так, чтобы она максимально соответствовала тому размещению эталонов, с помощью которых производилось обучение. Тогда распознавание заработает правильно (рис. 2.15). Такой процесс "разглядывания" может предполагать:
поиск возможности совмещения условного центра элемента изображения и центра экрана - входного рецепторного слоя сети (фокусировка); поиск варианта масштабирования элемента изображения (приближение - удаление); поиск угла наклона и др.
В результате таких пробных действий может вдруг "запуститься" процесс распознавания, хотя, возможно, и ошибочного. Что ж, в жизни бывает и так.

Рис. 2.15. Поиск условия узнавания
Этот процесс выделения и размещения в попытке инициировать распознавание мы можем сравнить с концентрацией нашего внимания и с фокусировкой, понимая, что наше зрение в каждый момент всегда сконцентрировано на элементе изображения, держа его в фокусе, в целом производя обзор и разглядывание всего изображения [26].
Напомним, что работа нейросети тактируется. Тогда развитие сценария в увлекательной многофункциональной детской игре с обучаемым компьютерным человечком КОМПИ может быть таким, как представлено на рис. 2.16.

Рис. 2.16. Реакция на распознавание в реальном времени
Формализация нейросети
Тактирование работы сети, столь характерное для каждой управляющей системы, которая отслеживает состояние сети в дискретные моменты времени, определяет потактовое продвижение по ней волны возбуждений от входного слоя к выходному. Волна за волной, возбуждения имитируют систолическую схему вычислений - параллельный конвейер обработки отдельных кадров, соответствующих конфигурации возбуждений входного слоя в одном такте.
На практике широко исследуются многослойные сети типа персептрон, где отсутствуют обратные связи и связи возможны между нейронами только смежных слоев. В данном разделе мы также не рассматриваем обратные связи, но снимаем ограничение на "слоистость" нейросети, обеспечивая более общий подход. Именно такая нейросеть, допускающая связи "через слой", была построена в приведенном выше примере. Для таких сетей значительно упрощаются следующие построения.
Нейронную сеть можно изучать статически, исследуя ее структуру, и динамически, исследуя в ней прохождение возбуждений.
Статические исследования нейросети показывают, что она представляет собой ориентированный граф G без контуров. Вершины его соответствуют нейронам, дуги - синапсическим связям. Целесообразно такой, высший уровень представления отделить от более глубокого описания каждого нейрона и связей между ними, отображающего динамику проходящих процессов, т.е. расчет значения возбуждения нейронов в зависимости от весов синапсических связей и порогов.
Граф малопригоден для формальных исследований и компьютерных алгоритмов. Удобнее пользоваться матричным отображением нейросети. Таким способом представления можно отобразить как структуру, конфигурацию, топологию графа, так и численные значения характеристик его синапсических связей.
Составим матрицу следования S (рис. 3.9), число строк (и столбцов) которой равно числу нейронов сети, включая нейроны входного и выходного слоя. Каждая строка (и столбец с тем же номером) соответствуют одному нейрону.
Элемент (i, j) этой матрицы - суть непустой объект, содержащий вес ?ij синапсической связи j

В то же время элементы матрицы S следует интерпретировать как булевы переменные, равные "1" в случае ненулевого значения указанного веса. Это разрешает выполнение логических операций над строками и столбцами матрицы S, рассматривая ее как аналогичную матрицу следования, используемую при описании частично упорядоченных множеств работ в параллельном программировании [6].

Рис. 3.9. Матрица следования с транзитивными связями
Матрицу S можно изучать в статическом режиме, исследуя и корректируя возможные пути прохождения возбуждений. По этой же матрице в динамическом режиме (моделирования) можно исследовать действительные пути прохождения возбуждений. Такое исследование связано с потактовым расчетом величин возбуждения нейронов.
Нулевые строки (входы) матрицы S соответствуют нейронам входного слоя - рецепторам, нулевые столбцы (выходы) - нейронам выходного слоя.
Нейроны образуют статические цепочки









Пусть по статической цепочке i




Алгоритм дополнения матрицы S транзитивными связями весьма прост.
Для всех i = 1, 2 ,…, N:
Формируем новое значение строки i логическим сложением этой строки со строками, соответствующими непустым элементам в ней. "Новые" непустые элементы заменяем на не пустые элементы, обозначающие транзитивные связи.
В нашем примере матрица S, дополненная транзитивными связями (непустые клеточки), и представлена на рис. 3.9.
Зафиксируем некоторое подмножество R нейронов входного слоя и единственный нейрон r выходного. Построим множество цепочек, ведущих из выделенного подмножества нейронов входного слоя в данный нейрон выходного слоя. Выделенное таким образом множество цепочек назовем статическим путем возбуждения данного нейрона выходного слоя по множеству нейронов входного слоя. Обозначим его R

Представим алгоритм формирования статического пути возбуждения R

Вычеркиваем из матрицы следования S строки и столбцы, которые соответствуют нейронам, не принадлежащим R.Вычеркиваем из матрицы следования S все строки и столбцы, отображающие нейроны выходного слоя, кроме нейрона r.Вычеркиваем из матрицы следования S строки и столбцы, отображающие нулевые позиции строки нейрона r.Вычеркиваем из матрицы следования S строки и столбцы, отображающие нейроны внутренних слоев нейросети, в том случае, если в результате предыдущего вычеркивания эти строки оказались нулевыми.Выполняем пункт 4, пока не прекратится образование нулевых строк.
На рис. 3.10 матрицей S[B1, A1, C1



Рис. 3.10. Статический путь возбуждения
Теперь рассмотрим фактор возбуждения и проанализируем возможные динамические пути прохождения возбуждений.
Динамической цепочкой возбуждений ?1



Динамическая цепочка возбуждений является вырожденной, если ее последний элемент обладает нулевой величиной возбуждения. Вырожденная динамическая цепочка возбуждений характеризует затухание сигнала.
Предъявим сети некоторый образ или эталон (не будет большой ошибки, если и здесь при предъявлении мы будем пользоваться словом "образ", ибо все есть образ чего-то), приводящий к возбуждению нейроны входного слоя, - в некоторой конфигурации.Эти нейроны образуют множество R. В результате возбуждения сети оказался возбужденным некоторый нейрон r выходного слоя. Сформировался, таким образом, динамический путь возбуждения R


В общем случае не все нейроны, составляющие статический путь возбуждения, "работают" на возбуждение нейрона выходного слоя, поскольку возможны вырожденные динамические цепочки возбуждения, обусловленные значениями порогов передаточной функции.
Модель механизма запоминания
Главный механизм запоминания, реализованный в природе, можно представить так. Импульс возбуждения, проходя через синапс, "нагревает" и уменьшает его сопротивление, увеличивая синапсический вес. В последующих тактах, при последующих предъявлениях эталона, импульс возбуждения увереннее одолевает путь возбуждения, с большей определенностью указывая соответствующий образ (как говорится, "Сложилась связь"), а используемые при этом синапсы, "подогреваясь", сохраняют и, возможно, увеличивают вес.
Здесь работает известное правило Хебба [19, 20]: Синапсический вес связи двух возбужденных нейронов увеличивается.
Таким способом даже достигается эффект локализации и максимизации возбуждения на выходном слое, дублирующий, а возможно, исключающий необходимость взаимодействия соседних нейронов.
По-видимому, синапсы обладают свойством "остывания" со временем, если нет подтверждения их использования. Такое предположение адекватно свойству нашей памяти: ненужная, не подтверждаемая и не используемая периодически информация стирается ("Связи рвутся!"). Стирается до такой степени, что приходится учиться заново.
Отметим и важную роль воображения: эталоны на входном слое поддерживаются достаточно долго, возобновляются или моделируются. По-видимому, здесь большое значение имеет эпифиз, "третий глаз" - орган воображения и медитации, память и генератор видений.
При создании искусственных механизмов обучения нейросети возникают вопросы:
Увеличивать ли веса всем нейронам, образующим статический путь возбуждения - для запоминания эталона?Увеличивать ли веса только вдоль некоторых (опорных) цепочек статического пути возбуждения? Увеличивать ли веса только нейронов, образующих динамический путь возбуждений; ведь выше предполагалось, что уже само возбуждение увеличивает вес связи? Зачем возбуждать дополнительные нейроны, если и этих достаточно?
По-видимому, третий аспект в большей степени соответствует самообучению, самонастройке. Вмешательство в наш мозг на этом уровне исключено.
Однако система искусственного интеллекта - в более выгодном положении. Ведь она находится под нашим неусыпным контролем, реализуя обучение "с учителем", и допускает любое вторжение, корректирующее вынужденные недостатки естественного интеллекта. Поэтому, рассматривая пример (и пытаясь накопить хоть какой-то опыт), мы будем увеличивать веса синапсических связей нейронов, составляющих выделенные цепочки статического пути возбуждения от эталона к образу. Назовем такой метод методом опорных путей, который выработан в процессе проведения многочисленных экспериментов. В частности, увеличение синапсических весов большого числа нейронов приводило к неудачам, связанным с корреляцией динамических цепочек возбуждения для разных эталонов и с быстрым насыщением нейросети (недостаток многих известных алгоритмов обучения). В процессе обучения многим эталонам рано или поздно все веса сети оказывались повышенными, и она прекращала что-либо различать. Начиналась путаница согласно выражению "Ум за разум заходит!"
Что же касается величины изменения синапсических весов, то вряд ли необходимо относительно каждого нейрона решать системы дифференциальных уравнений в частных производных. (Речь идет о методе обратного распространения ошибки, подробно изложенном в [20].) Природа больше рассчитывает на авось, "на глазок" и другие мудрые и практические приблизительные ориентиры, малопривлекательные теоретически. В данном случае нас более обнадеживает "прилив крови" в нужном направлении, стимулируемый информационным раздражителем или легким подзатыльником. В связи с этим введем некую переменную

Таким образом, нам удалось перейти от схемотехники к нейротехнологии, от точного, определенного к приблизительному, неопределенному. Действительно, не могла эволюция, основанная на принципе "делай все, что можно", методом "проб и ошибок" привести к производству точных электронных схем, упрятанных в черепную коробку.Да и нет в природе точной, абсолютно достоверной информации. Но общие логические принципы и зависимости должны быть воплощены и в той и в другой технологии.
Начинаем решать пример
"В России революция - дрогнула мать
сыра земля, замутился белый свет…"
Артем Веселый, "Россия, кровью умытая"
Нейросетевые технологии основаны на моделировании деятельности мозга. А как сказал Р. Шеннон, "Моделирование есть искусство" [29]. И как любое искусство, модель нейросети может базироваться на примерах, опыте и общих рекомендациях.
Рассмотрим пример, который навеян славным временем революционной перестройки, предлагающей нам эталоны актуальности, культурного ориентира и предприимчивости.
Вася и Петя - друзья. Нет, не в том смысле: они почти нормальной сексуальной ориентации. Скорее в смысле вечной святой мужской дружбы, без смущения применяющей слово "друг". Обозначим А - множество друзей,

Вася и Петя - крутые парни. Они плохо учились в школе, и это хорошо! Они создали "крышу", под которой успешно трудится ряд палаток

заботливо опекаемые хозяйками, соответственно, Оксаной и Роксаной, Мариной и Региной, а также Аполлинарией. Палатки реализуют продукцию фирм

Фирма Красный Киллер в секретных подвалах славных подразделений бойцов холодной войны на основе бабушкиного самогона и контрабандного синтетического спирта гонит всемирно известную вино-водочную продукцию отличного качества. Фирма Пират производит аудио- и видеопродукцию и другие культурные ценности. Фирма Ночная Бабочка стряпает французскую косметику из мосластых московских дворняг.
Ситуацию контролирует дядя Рамзай из налогового ведомства, который имеет свой маленький частный бизнес. С каждой сложившейся ситуацией, определяемой тем, кто из друзей какие палатки "накрыл" и чья продукция находилась на реализации, дядя Рамзай связывает свою долю прибыли, основанную, мягко говоря, на шантаже. Дядя Рамзай имеет свой штат осведомителей: пару бомжей - жертв предыдущей амнистии, и пару-тройку голопузых апологетов трудного детства, которые с некоторой долей достоверности, за небольшую мзду и мелкое попустительство, доставляют ему информацию.
Дядя Рамзай - прогрессивный бизнесмен, и оценки прибыли решает проводить на высоком математическом уровне, обратившись за помощью к нам (рис. 3.1). Мы хорошо учились в школе, и это - плохо! Мы, как истинные альтруисты и ученые-бессеребренники, с радостью поможем ему, - бесплатно.

Рис. 3.1. Предмет исследования
А информации приходится обрабатывать дяде Рамзаю много. Он, прямо скажем, работает в условиях неопределенности и усиленных помех. Судите сами. Оксана делит любовь между Васей и Петей. Роксана - пока нет. Марина и Регина, жалея, подкармливают юных следопытов. Аполлинария вообще закадрила хахаля из местной мэрии и разъезжает в длиннющем "линкольне". Тщетно пытаясь разрушить узы бескорыстной дружбы, фирма Пират напрямую подмазала Васю, снизив нагрузку вымогательства на свою продукцию. Петя, кажется, пошел на нарушение Конвенции и вторгается в область, контролируемую конкурентами. (Ох, не избежать благородной разборки, со стрельбой и окровавленными трупами!) Скоро отмотает свой срок Никита, и предприятие расширится и т.д., и т.д., и т.д.…
Все такие обстоятельства прямо или косвенно влияют на долю прибыли дяди Рамзая.
Однако, разбираясь в столь сложной ситуации - для демонстрации действительно очень трудно формализуемой задачи, - мы чувствуем, как чем-то липким покрываются наши честные ладошки. А потому мы решительно отталкиваемся от… и со сладким упоением возносимся на уровень милого сердцу абстрактного, математического, формально-логического мышления.
Но, прежде всего, принимая столь ответственный заказ, мы хотим четко уяснить, что хочет дядя Рамзай, - чтобы все же максимально формализовать задачу. И после долгих согласований мы устанавливаем:
Он хочет, задавая исходную информацию на входе той системы, которую мы для него создадим, на основе, возможно, не полной или недостоверной информации своих агентов, все-таки распознать с наибольшей определенностью, что это за ситуация (на какую ситуацию в наибольшей степени указывают сложившиеся обстоятельства), чтобы знать, на какой навар можно рассчитывать.Он хочет, задавая исходную ситуацию на входе системы, установить среднюю величину прибыли (учитывая, что в разной степени речь идет о нескольких возможных ситуациях).Он хочет сделать вывод о частоте появления различных ситуаций, чтобы перераспределить тарифные ставки за умолчание о шалостях Васи и Пети.
Итак, ступим на путь абстрагирования.
Пусть по стечению обстоятельств, которые мы будем называть событиями, принимаются решения. Решения образуют конечное множество. Каждое решение соответствует некоторой, в общем случае не единственной, комбинации событий. Предположим наличие нескольких вариантов одного события.
Введем "удобную", не обязательно единственно возможную, иерархию событий на основе их совместимости и алгоритмически привычного представления.
Считая, что варианты каждого вида событий образуют исчерпывающее множество, алгоритм работы системы можно записать как
if A1 then if B1 then R1 else if (C1


Здесь R1-R5 - принимаемые решения.
Одно решение соответствует некоторой, в общем случае не единственной, комбинации событий. Для изображения таких комбинаций воспользуемся записями, например, вида А1








Проанализировав и перебрав все возможные ситуации, с учетом одинакового принимаемого решения, получим систему логических высказываний - предикатов, как основу формализации задачи при построении нейросети:
 | (3.1) |
Второе логическое высказывание означает: "Если Вася посетил одну из палаток С1, С2 или С3, торгующих сегодня продукцией фирм В2 и (или) В3, то следует принять решение R2" и т.д.
Нейросеть произвольной структуры
Предположим, мы располагаем некоторым банком "красиво" изображенных графических схем, которые можно положить в основу структуры нейросети. Понравившуюся структуру мы решаем интерпретировать как нейросеть, дополнив ее передаточной функцией и обучив решению задачи, поставленной дядей Рамзаем.
Пусть выбранная нами нейросеть имеет 12 входов (более чем достаточно), 5 выходов и реализует ту же передаточную функцию с начальными значениями весов ?ij = 0 и порога h = 0.
Однако сеть обладает специфической топологией, затрудняющей ее обучение. Сеть многослойная, что исключает связи "через слой", присутствующие, например, на рис. 3.7 как результат построения нейросети "под задачу". Да и связь между слоями скорее соответствует известному предупреждению "шаг влево, шаг вправо…".
Будем использовать метод опорных путей, или трассировки, расширяющий использованный выше "схемотехнический" подход. Его можно изобразить схемой рис. 3.2



Итак, для успешной, наглядной и легко рассчитываемой трассировки решим вопрос кардинально: какие веса полагать равными нулю, а какие - единице? Все прочие возможности, например min ?ij = 0,1, введение порога h = 0,5 и т.д., будут способствовать более плавной работе сети, непрерывности перехода из состояния в состояние.
Применив принципы комбинаторики и эвристики, выполним трассировку нейросети (рис. 3.13). На рисунке наглядно показано, какая нейросеть была предоставлена, насколько она "неповоротлива", скажем, по сравнению с однослойной "каждый с каждым".

Рис. 3.13. Результат трассировки многослойной нейросети
Далее будет представлен формальный алгоритм трассировки. Однако чтобы настроиться на его понимание, следует проанализировать свои действия и сделать следующие выводы:
Мы анализировали слой за слоем, постоянно помня цель - пять комбинаций ситуаций, каждая из которых должна возбудить один из нейронов выходного слоя, не вводя пока жесткое закрепление решений за этими нейронами.В каждом слое мы собирали частную комбинацию - терм, который можно использовать в последующем, - из доступных термов предыдущего слоя.Термы, которые пока не могут быть использованы при конструировании из-за их взаимной удаленности, мы запоминали без изменения на анализируемом слое, пытаясь их "подтянуть" в направлении возможного дальнейшего объединения.Мы старались не "тянуть" термы "поперек" всей сети. В противном случае мы сталкивались бы с проблемой: как избегать пересечений и искажения уже сформированных термов. Все это заставило нас долго не закреплять нейроны выходного слоя за решениями, что в конце концов привело к нарушению естественного порядка следования решений.
Для автоматизации трассировки необходимо матричное представление, только и доступное компьютеру.
Матрица следования, отражающая трассировку нейросети, получается на основе рис. 3.13, если отметить элементы, соответствующие "тонким" линиям, нулевыми весами, а элементы, соответствующие "жирным" линиям, - весами, равными единице.
На рис. 3.14 отражен динамический путь возбуждения, приводящий к решению R1. Он строится по алгоритму, изложенному в разд. 3.5. В данном случае динамические пути возбуждения совпадают со статическими. В общем случае из статического пути возбуждения необходимо исключить нейроны, которые не входят во входной слой и которым соответствуют нулевые строки сформированной матрицы следования.

Рис. 3.14. Динамический путь возбуждения
Аналогично получают динамические пути возбуждения, приводящие к другим решениям.
Поставим теперь задачу дальнейших исследований: как построить все необходимые пути возбуждения так, чтобы они, возможно, пересекались, - но только для формирования общих термов? А способна ли выбранная нами "готовая" нейросеть вообще справиться с поставленной задачей или предпочтительнее принцип "нейросеть под задачу"?
…Вот теперь-то мы довольны! Мы снабдили дядю Рамзая универсальной обучаемой нейросетью. Теперь, если он, раскаявшись, вновь возлюбит свою благороднейшую профессию, он найдет ей (сети) достойное применение в водворении Васи, Пети & K0 на то спальное место, которого они действительно заслуживают.
Нейросетевые технологии и нейрокомпьютеры
Итак, располагая знаниями о ситуациях на входе управляющей системы и реакциях на каждую из них, получаем таблицу. В одном столбце, так называемом запросном поле, - вектор-ситуация, в другом, ответном поле - принимаемое решение. Такая идея ситуационного управления высказана Д.А. Поспеловым [23] еще в 1970-х годах.
Для ее воплощения можно применить технологии построения ассоциативной памяти, столь широко используемой в современных вычислительных системах. Если между ситуациями ввести операции отношения, то можно построить операции вида "найти ближайшую величину слева (справа)", "найти ближайшие включающие границы" и т.д. Идея ассоциативной ЭВМ давно реализована, например в STARAN [15] (1977 г.).
На основе вышесказанного строится самообучающаяся система, в режиме обучения дополняющая базу знаний (ту самую таблицу в ассоциативной памяти) с помощью моделирования ситуаций и принимаемых решений и выдающая решение в рабочем режиме согласно таблице на основе интерполяции.
Однако необходимость выхода на большие размерности ограничивает возможность построения "большой" ассоциативной памяти по существующей технологии. Ведь такая память, даже при реализации единственной операции, основана на одновременном сравнении входного вектора с запросными частями всех ее регистров и с выдачей содержимого ответного поля в случае совпадения.
Выходит, что мозг не может непосредственно хранить таблицы, а моделирует их с помощью нейросетевых механизмов? Можно вспомнить, что исходные предложения (например, Кохонена) по применению нейросетей касались именно ассоциативной памяти.
Зачем же нам следовать столь неловкому воплощению?
Ответ может быть лишь таким: все хорошо к месту. Просто более тщательно следует определять области разумного применения каждого из различных средств решения задач искусственного интеллекта. И как можно раньше уйти от опасных для здоровья вопросов философски-мистического характера.
Хотя и следует вновь заглянуть "в зеркало".
Где мы используем принцип нейросети непосредственно, а не косвенно, - посредством расчета, анализа баз знаний и т.д.? По-видимому, обязательно там, где мы получаем первичную информацию для последующих выводов: органами зрения, слуха, обоняния, осязания.
На этом же уровне мы способны провести первичную классификацию и принять оперативное решение: убежать от стремительно приближающегося автомобиля, надеть противогаз и т.д.
Значит, в нашей жизнедеятельности, требующей разнообразного проявления, существует такая ниша, эффективная на самом низком уровне животного состояния, где решение должно быть сверхоперативным, скорее - рефлекторным, не допускающим анализа. Этому способствует высокий параллелизм сети. Именно высокий параллелизм, наряду с исключением сложных расчетов, обусловил взрыв интереса к системам искусственного интеллекта в начале 1980-х годов, когда остро встала задача разработки вычислительных средств сверхвысокой производительности.
И этим мы вновь затронули важный вопрос актуальности аппаратной реализации нейросети или нейрокомпьютеров, т.к. программная модель на непараллельном компьютере лишена свойства высокого параллелизма мозга и ограничивает выход на "большие" нейросети.
Этот параллелизм выражается в том, что одновременно обрабатывается большое число цепочек нейронов. При этом каждый нейрон обрабатывается хотя и по одному алгоритму, но - по разным его ветвям: один, в конце концов, возбудится, другой нет; связи нейрона индивидуальны и изменяются не идентично связям других нейронов и т.д.
Тогда, ставя задачу разработки параллельного вычислительного устройства - нейрокомпьютера, способного имитировать работу нейросети с учетом ее достоинств по реализации высокой производительности, следует учесть, что:
необходимо распределять нейроны (точнее, нейроподобные элементы или соответствующие им программные процедуры) между процессорами НК, синхронизируя обработку нейронов в соответствии с матрицей следования. Т.е. необходимо реализовать способ распараллеливания по информации;одинаковые на всех процессорах программы одновременно обрабатываемых нейронов в общем случае должны выполняться по разным ветвям.
При программной реализации нейросети перечисленные требования соответствуют SPMD-технологии ("одна программа - много потоков данных") [9], привлекательность которой обоснована для многих приложений параллельного решения задач высокой сложности.
Привлекательна реализация "большой" нейросети на основе сетевых технологий.
При аппаратной реализации НК ( или его аппаратной поддержке) также необходимо учесть следующее требование: один нейроподобный элемент должен делить время между имитацией многих нейронов. Жесткая аппаратная имитация нейросети, соответствующая связи "один нейроподобный элемент - один нейрон", неэффективна, т.к. ограничивает возможную размерность моделируемой сети.
Учитывая специализацию нейрокомпьютера при применении сетевых технологий в рамках построения более сложных управляющих систем, целесообразно, чтобы НК использовался как сопроцессор под управлением мощного и универсального компьютера-монитора. Это же обусловлено разнообразными функциями "учителя" по формированию, заданию и регулировке параметров, по обучению и по дальнейшему применению результатов. В рамках сегодняшних компьютерных технологий НК должен дополнять персональный компьютер как его внешнее устройство и "врезаться" в существующие ОС.
***
Итак, мы знаем языки логического вывода, экспертные системы, самообучающиеся системы управления. Но в природе первично воплощены лишь нейросети!
Почему же мы, располагая столь богатым арсеналом средств искусственного интеллекта, в основе своей (как нам кажется!) опирающихся далеко не на одни только нейросети, самодовольно недоумеваем, отчего они не были первоначально заданы Природой, а явились плодом нашей творческой гениальности? И мы кощунственно вопрошаем:
- Ты что, Господи, не мог додуматься до этого Сам?
И посылается нам догадка с Неба: о Великой Целесообразности, о непрерывности и преемственности Развития, о предлагаемом Базисе, требующем Надстройки, о вечной Причинно-Следственной Вытекаемости… Мозг - конструктивно целесообразен, развиваем, универсален, самодостаточен. Мозг - основа, на которой еще не то можно построить!
Здесь можно привести пример колеса, не существующего в живых организмах. Какова должна быть длина нерва, чувствующего обод колеса? Значит, колесо должно быть отделено от живого существа! Но не рожать же матери отдельно ребенка, отдельно - колесо к нему.И сказал Господь Человеку:
- Я дам тебе разум, а колесо ты сделаешь сам…
Нет, додумался Он, Высший Разум, - посредством средства, вложенного в нас… Мы сыграли роль слепых исполнителей предназначенного, предопределенного, предсказанного… Словно микробы в желудочно-кишечном тракте - в заблуждении о личном счастье и сытости, - в действительности мы работаем на Волю Создателя, помогая Ему в главной и глобальной установке на Развитие.
Однослойная нейросеть
Для наглядности воспользуемся как матричным, удобным алгоритмически, так и графическим представлением нейросети.
Однослойная нейросеть, составленная по принципу "каждый с каждым", представлена на рис. 3.11.

Рис. 3.11. Формирование однослойной нейросети
Пусть используется предложенная выше передаточная функция

Значения ?ij предстоит подобрать, а значения hi положим равными нулю.
Закрепим 10 нейронов входного слоя за исходными данными, 5 выходов - за решениями. Этим мы выделим интересующую нас подсеть, которой соответствует матрица следования на рис. 3.12.

Рис. 3.12. Матрица следования для однослойной нейросети
Здесь отображен ее окончательный вид, т.к. сначала все веса связей принимаются равными нулю.
Для того чтобы сформировать решение R1 на нейроне Вых1, надо значительно увеличить веса связей этого нейрона с нейронами В1, А1, С1, С2, С3, С4, С5, т.е. построить статический путь возбуждения [B1, A1, C1, C2, C3, C4, C5]

В данном случае результат очевиден, поэтому обратим внимание на некоторый общий подход.
Установим веса связей между нейронами В1, А1, С1, С2, С3, С4, С5 с одной стороны, и нейроном Вых1 - с другой равными единице, оставив нулевыми веса связей этого нейрона с другими нейронами входного слоя. Таким образом полностью исключается влияние других нейронов входного слоя на данный выходной нейрон. Конкретная задача может потребовать корректировки, учета взаимного влияния всех входных ситуаций в результате тщательного экспериментального исследования задачи.
Здесь вновь прослеживается преимущество нейросети, способной элементарно просто учитывать наблюдаемые или интуитивно предполагаемые поправки, требующие огромных исследований и расчетов.
Поступив так же со всеми выделенными нейронами выходного слоя, получим окончательный вид матрицы следования (рис. 3.12). Построенная нейросеть полностью соответствует специальной сети "под задачу", представленной на рис. 3.7.
…Так какую же сеть предложить дяде Рамзаю? Ведь надо и подоходчивее, и попрактичнее, но и так, чтобы не казалось уж слишком просто.
Построение нейросети "под задачу"
Мы построили нейросеть - с экзотическими (с точки зрения невропатолога) конъюнкторами и дизъюнкторами.
Предположим теперь (рис. 3.5, 3.6), что все нейроны одинаковы, реализуют одну передаточную функцию, а веса и пороги реализуют равные и общие возможности.
Введем ту же, но без ограничения по величине возбуждения, передаточную функцию

Положим ?ij = 0,8, h = 0,2. Сеть представлена на рис. 3.7.

Рис. 3.7. Расчет примера на нейросети
Подадим на вход, например, ситуацию {A1, B1, C3}, требующую решения R1. Величины возбуждений нейронов показаны на рисунке.
На основе расчетов по полученной сети составим табл. 3.1, отображающую правильную (!) работу сети при получении различных решений. При этом связи, предыстория которых определена дизъюнкторами, требуют проверки не более чем одного "представителя": в рассмотренном примере получаем тот же результат, если вместо С3 положим С1 или С2.
| 1,144 | 0,76 | 0,28 | 0,024 | 0,248 |
| 0,504 | 1,144 | 0,664 | 0,024 | 0,248 |
| 0,504 | 1,144 | 0,664 | 0,504 | 0,024 |
| 0,504 | 0,664 | 1,144 | 0,024 | 0,224 |
| 0,504 | 0,664 | 1,144 | 0,504 | 0,024 |
| 0,024 | 0,504 | 0,024 | 1,144 | 0,504 |
| 0,504 | 0,28 | 0 | 0,504 | 0,888 |
| 0,024 | 0,024 | 0,504 | 0,504 | 0,888 |
| 0,824 | 0,529 | 0,593 | 0,312 | 1,003 |
Анализируя первые восемь строк таблицы, соответствующие достоверным ситуациям, видим, что по крайней мере максимум возбуждения определяется устойчиво верно.
Рассмотрим ту же неопределенную ситуацию. Она отражена в последней строке таблицы. Близка ли она более всего ситуации, когда Петя направился к Аполлинарии и надо принимать решение R5? Ситуация с Васей, устремившимся туда же, дает примерно тот же ответ.
Отметим, что по убыванию величин возбуждения нейронов выходного слоя, вновь полученный результат полностью совпадает с полученным по "схемотехнической" сети (рис. 3.5), так что и величина средней прибыли, по-видимому, будет близка найденной ранее.
Однако не проще было бы применять способ построения нейросети, близкий к табличному? Что, если каждую ситуацию непосредственно "замкнуть" на соответствующее решение, избежав сложной путаницы промежуточных слоев нейронов и не рассчитывая множества вариантов для нахождения максимального возбуждения и распределения возбуждения на выходном слое?
Очень часто на практике так и поступают. Поэтому широкое распространение получили так называемые однослойные сети. Построим такую сеть и для нашего примера (рис. 3.8).

Рис. 3.8. Однослойная нейросеть
Возьмем ту же передаточную функцию, с теми же параметрами и рассчитаем те же примеры, отображенные в табл. 3.1. Составим для них табл. 3.2.
Данная нейросеть также оказывает предпочтение решению R5, хотя порядок убывания величин возбуждения выходного слоя отличен от ранее полученного. Предпочтительность решений R2 и R3 меняется местами.
| 2,2 | 1,4 | 0,6 | 0,6 | 1,4 |
| 1,4 | 2,2 | 1,4 | 0,6 | 1,4 |
| 1,4 | 2,2 | 1,4 | 1,4 | 0,6 |
| 1,4 | 1,4 | 2,2 | 0,6 | 1,4 |
| 1,4 | 1,4 | 2,2 | 1,4 | 0,6 |
| 1,4 | 1,4 | 0,6 | 2,2 | 1,4 |
| 1,4 | 0,6 | 0 | 1,4 | 2,2 |
| 0,6 | 0,6 | 1,4 | 1,4 | 2,2 |
| 2,04 | 1,4 | 0,84 | 1,4 | 2,68 |
Применение "готовых" нейросетей
Справедливо желание построения универсальных моделей нейросетей в составе программного обеспечения компьютера, снабженных механизмами приспособления под задачу пользователя. Еще более справедливо желание построить набор аппаратных средств - нейросетей (нейрокомпьютеров, НК), сопряженных с компьютером и, по выбору пользователя, участвующих в решении сложных задач. Такие аппаратно реализованные нейросети, как приставки или внешние устройства компьютера, например, определяют специальное направление использования ПЛИС - интегральных схем с программируемой логикой.
"Схемотехнический" подход к построению нейросети "под задачу"
Реализуем подход, используемый при построении схем устройств компьютера и другой электронной техники. Выделим функционально полную, для данного применения, систему булевых функций - дизъюнкцию


Отрицание нам не понадобится, мы пока не рассматриваем тормозящие связи.
Нарушив принятые обозначения, построим (рис. 3.2) схему, реализующую алгоритм счета значения выражения (3.1). Предполагаем, что на вход будут подаваться значения булевых переменных, обозначающих события.

Рис. 3.2. "Электронная" схема системы принятия решений
Такая электронная схема могла бы нам верно служить, способствуя быстрому определению необходимой реакции на сложившуюся ситуацию, если мы предусмотрели все возможные ситуации, знали, какое решение соответствует каждой из них, и всегда обладали полной и точной информацией о происходящих событиях. Но ведь не зря мы обращаем внимание на те помехи и неопределенность, в условиях которых приходится жить и работать. Мы должны оперировать только достоверностями либо другими оценками событий, пытаясь определить, какой ситуации более всего соответствуют сложившиеся обстоятельства.
Значит, мы должны из точного, детерминированного представления перейти в область ассоциативного, неточного, приблизительного мышления! Но степень (частота) угадывания должна быть достаточно высока.
Именно здесь должна помочь нейросеть.
Прежде всего надо перейти от типа булевых переменных к типу действительных, введя в обращение не непреложность событий, а лишь вероятности или другие весовые оценки их наступления (электронной технике это не свойственно). Затем необходимо реализовать аналоги булевых функций над этим новым типом данных, т.е. заставить нейроны с помощью весов, порогов и самой передаточной функции выполнять дизъюнкции и конъюнкции с учетом вариации и неопределенности данных. При этом абсолютно достоверные данные, несомненно, приведут к известным решениям, а по неточным данным можно определить лишь вес каждого из возможных решений.
Реализуем подход, используемый при построении схем устройств компьютера и другой электронной техники. Выделим функционально полную, для данного применения, систему булевых функций - дизъюнкцию


Отрицание нам не понадобится, мы пока не рассматриваем тормозящие связи.
Нарушив принятые обозначения, построим (рис. 3.2) схему, реализующую алгоритм счета значения выражения (3.1). Предполагаем, что на вход будут подаваться значения булевых переменных, обозначающих события.

Рис. 3.2. "Электронная" схема системы принятия решений
Такая электронная схема могла бы нам верно служить, способствуя быстрому определению необходимой реакции на сложившуюся ситуацию, если мы предусмотрели все возможные ситуации, знали, какое решение соответствует каждой из них, и всегда обладали полной и точной информацией о происходящих событиях. Но ведь не зря мы обращаем внимание на те помехи и неопределенность, в условиях которых приходится жить и работать. Мы должны оперировать только достоверностями либо другими оценками событий, пытаясь определить, какой ситуации более всего соответствуют сложившиеся обстоятельства.
Значит, мы должны из точного, детерминированного представления перейти в область ассоциативного, неточного, приблизительного мышления! Но степень (частота) угадывания должна быть достаточно высока.
Именно здесь должна помочь нейросеть.
Прежде всего надо перейти от типа булевых переменных к типу действительных, введя в обращение не непреложность событий, а лишь вероятности или другие весовые оценки их наступления (электронной технике это не свойственно). Затем необходимо реализовать аналоги булевых функций над этим новым типом данных, т.е. заставить нейроны с помощью весов, порогов и самой передаточной функции выполнять дизъюнкции и конъюнкции с учетом вариации и неопределенности данных. При этом абсолютно достоверные данные, несомненно, приведут к известным решениям, а по неточным данным можно определить лишь вес каждого из возможных решений.
Тогда по максимальному весу определим, на что более всего похожа данная неопределенная ситуация.
Выберем передаточную функцию произвольного (i-го) нейрона, с числом m входов-дендритов:

где ?(x) = x при x

Здесь Vj, как всегда, - величина возбуждения (другого нейрона), поступающая на j-й вход.
Тогда нейрон-конъюнктор может быть реализован с помощью существенно высокого порога (рис. 3.3), где значение


Рис. 3.3. Модель нейрона-конъюнктора
При обучении предполагается, что входные сигналы - булевы переменные, принимающие значения 0, 1. Положим ?ij = 1/m и выберем

При переходе к действительным переменным, когда вместо событий рассматриваются, например, лишь предполагаемые вероятности их наступления, экспериментальный выбор значения

Нейрон-дизъюнктор реализуется, наоборот, при низком значении порога, но при высоких значениях весов. Порог выбирается так, чтобы уже при возбуждении на одном входе возникал сигнал возбуждения на выходе. При этом сигнал на выходе не превышает "1" (рис. 3.4).

Рис. 3.4. Модель нейрона-дизъюнктора
Понятно, что при полной определенности в режиме обучения возбуждение поступает по единственному входу (нейрон реализует функцию "ИСКЛЮЧАЮЩЕЕ ИЛИ"). В условиях неопределенности предполагается, что нейрон имитирует выполнение функции "ИЛИ", допуская возбуждение более чем на одном входе.
Итак, поменяем тип данных и заменим нейронами все элементы на схеме рис. 3.2. Получим нейросеть на рис. 3.5, где нейроны-конъюнкторы заштрихованы.
Теперь позволим дяде Рамзаю поучиться, поэкспериментировать, задавая различные достоверности событий, - возможных или невозможных.
Например, зададим "правильную" и абсолютно достоверную ситуацию В3 = 1, А1 = 1, С4 = 1 (Вася отправился к Регине, торгующей ямайским ромом). Легко проследить, что в первом такте возбудятся нейроны 1 и 6, реализующие дизъюнкцию. Величина их возбуждения равна "1". В следующем такте возбуждение нейронов 1, 6 и А1 приведет к возбуждению (с величиной, равной "1") нейронов 7 и 9, а в следующем такте - сигналы возбуждения нейронов 6 и 7 поступят на вход нейрона-конъюнктора Вых3. Никакой другой нейрон выходного слоя не возбудится.

Рис. 3.5. Нейросеть с "конъюнкторами" и "дизъюнкторами"
Рассмотрим другую ситуацию, неопределенную и недостоверную.
Пусть то ли Вася, то ли Петя - "разведчик" не установил точно - направился то ли к Оксане, то ли к Аполлинарии, торгующим в этот день то ли тройным одеколоном, то ли золотым диском группы "Та-ра-рам".
Дядя Рамзай, по выданной нами инструкции, решает использовать интуитивные оценки веса или, на нашем языке, оценить достоверность каждой компоненты возникшей ситуации. Поскольку прогулки как Васи, так и Пети одинаково достоверны, то дядя Рамзай полагает величину возбуждения нейронов А1 и А2 равной 0,5 (VA1 = VA2 = 0,5). После долгих раздумий он по наитию полагает VB1 = 0,8, VB2 = 0,8, VC1 = 0,7, VC5 = 0,8.
Замечание. Напоминаем еще раз, что требовать исчерпывающего множества событий и непременного выполнения нормировочного условия не обязательно. Достоверность может выбираться по наитию, на уровне чувств. Именно эти качества неопределенности, субъективности, наличия жизненного опыта и интуиции присущи механизмам ассоциативного мышления.
Сдавая нейросеть "в эксплуатацию", мы установили веса всех конъюнкторов равными 0,5, а дизъюнкторов - равными 1. Пороги конъюнкторов определяются значением


Рис. 3.6. Расчет примера
Важность данного примера требует повторения рисунка нейросети (рис. 3.6) с проставленными возле нейронов значениями сигналов возбуждения.
В итоге ситуация скорее всего имеет решение R5, и уж никак не R4. Однако ситуация, соответствующая решению R1, требует внимания.
Пусть при вполне определенной ситуации (все достоверности принимают значение "1") каждое решение Ri приносит прибыль Mi. Тогда средняя величина ожидаемой прибыли для нашей неопределенной ситуации рассчитывается так:

Конечно, полученное решение столь же неопределенно, как и тот карточный расклад, что предвещает трогательную встречу в казенном доме, поэтому мы погружаемся в дальнейший поиск.
Тогда по максимальному весу определим, на что более всего похожа данная неопределенная ситуация.
Выберем передаточную функцию произвольного (i-го) нейрона, с числом m входов-дендритов:

где ?(x) = x при x

Здесь Vj, как всегда, - величина возбуждения (другого нейрона), поступающая на j-й вход.
Тогда нейрон-конъюнктор может быть реализован с помощью существенно высокого порога (рис. 3.3), где значение


Рис. 3.3. Модель нейрона-конъюнктора
При обучении предполагается, что входные сигналы - булевы переменные, принимающие значения 0, 1. Положим ?ij = 1/m и выберем

При переходе к действительным переменным, когда вместо событий рассматриваются, например, лишь предполагаемые вероятности их наступления, экспериментальный выбор значения

Нейрон-дизъюнктор реализуется, наоборот, при низком значении порога, но при высоких значениях весов. Порог выбирается так, чтобы уже при возбуждении на одном входе возникал сигнал возбуждения на выходе. При этом сигнал на выходе не превышает "1" (рис. 3.4).

Рис. 3.4. Модель нейрона-дизъюнктора
Понятно, что при полной определенности в режиме обучения возбуждение поступает по единственному входу (нейрон реализует функцию "ИСКЛЮЧАЮЩЕЕ ИЛИ"). В условиях неопределенности предполагается, что нейрон имитирует выполнение функции "ИЛИ", допуская возбуждение более чем на одном входе.
Итак, поменяем тип данных и заменим нейронами все элементы на схеме рис. 3.2. Получим нейросеть на рис. 3.5, где нейроны-конъюнкторы заштрихованы.
Теперь позволим дяде Рамзаю поучиться, поэкспериментировать, задавая различные достоверности событий, - возможных или невозможных.
Например, зададим "правильную" и абсолютно достоверную ситуацию В3 = 1, А1 = 1, С4 = 1 (Вася отправился к Регине, торгующей ямайским ромом). Легко проследить, что в первом такте возбудятся нейроны 1 и 6, реализующие дизъюнкцию. Величина их возбуждения равна "1". В следующем такте возбуждение нейронов 1, 6 и А1 приведет к возбуждению (с величиной, равной "1") нейронов 7 и 9, а в следующем такте - сигналы возбуждения нейронов 6 и 7 поступят на вход нейрона-конъюнктора Вых3. Никакой другой нейрон выходного слоя не возбудится.

Рис. 3.5. Нейросеть с "конъюнкторами" и "дизъюнкторами"
Рассмотрим другую ситуацию, неопределенную и недостоверную.
Пусть то ли Вася, то ли Петя - "разведчик" не установил точно - направился то ли к Оксане, то ли к Аполлинарии, торгующим в этот день то ли тройным одеколоном, то ли золотым диском группы "Та-ра-рам".
Дядя Рамзай, по выданной нами инструкции, решает использовать интуитивные оценки веса или, на нашем языке, оценить достоверность каждой компоненты возникшей ситуации. Поскольку прогулки как Васи, так и Пети одинаково достоверны, то дядя Рамзай полагает величину возбуждения нейронов А1 и А2 равной 0,5 (VA1 = VA2 = 0,5). После долгих раздумий он по наитию полагает VB1 = 0,8, VB2 = 0,8, VC1 = 0,7, VC5 = 0,8.
Замечание. Напоминаем еще раз, что требовать исчерпывающего множества событий и непременного выполнения нормировочного условия не обязательно. Достоверность может выбираться по наитию, на уровне чувств. Именно эти качества неопределенности, субъективности, наличия жизненного опыта и интуиции присущи механизмам ассоциативного мышления.
Сдавая нейросеть "в эксплуатацию", мы установили веса всех конъюнкторов равными 0,5, а дизъюнкторов - равными 1. Пороги конъюнкторов определяются значением


Рис. 3.6. Расчет примера
Важность данного примера требует повторения рисунка нейросети (рис. 3.6) с проставленными возле нейронов значениями сигналов возбуждения.
В итоге ситуация скорее всего имеет решение R5, и уж никак не R4. Однако ситуация, соответствующая решению R1, требует внимания.
Пусть при вполне определенной ситуации (все достоверности принимают значение "1") каждое решение Ri приносит прибыль Mi. Тогда средняя величина ожидаемой прибыли для нашей неопределенной ситуации рассчитывается так:

Конечно, полученное решение столь же неопределенно, как и тот карточный расклад, что предвещает трогательную встречу в казенном доме, поэтому мы погружаемся в дальнейший поиск.
Возбуждение входного слоя
Определим теперь возбуждение входного слоя, учитывая то, что по нейросетевым технологиям решаются сложные, чаще всего трудно формализуемые задачи. Исходная информация этих задач может быть настолько несовместима по смыслу, типам данных и единицам измерения, что приведение ее к некоторому количественному воплощению - величине возбуждения нейронов входного слоя - представляет серьезную проблему.
Например, как объединить величину превышаемой водителем скорости и тип автомобиля иностранного производства со вчерашним неудачным выступлением любимой автоинспектором футбольной команды, - при нахождении величины штрафа? Ведь каждый из перечисленных факторов должен определить некоторые общие, приведенные значения возбуждения.
Такое приведение также зависит от задачи. Поскольку нейроны - нечто стандартное для данной задачи или класса задач, то каждая характеристика нейрона - величина возбуждения, веса его синапсических связей, порог, передаточная функция - должны быть одинаковы или принадлежать общему (по каждой характеристике) для всех нейронов диапазону возможных значений.
Дадим рекомендации, основанные на "событийном" принципе.
В нашем новом примере о превышении скорости разобьем скорость на диапазоны штрафования, например, [90-100), [100-110), [110-120), [120-200]. За каждым диапазоном скорости закрепим нейрон входного слоя - рецептор. Определим его среднее значение возбуждения, равное 1. Пусть отклонение к границам диапазона скорости пропорционально уменьшает эту величину возбуждения, увеличивая величину возбуждения рецептора "соседнего" диапазона. Другой вариант задания исходных данных основан на решении вопроса принадлежности скорости некоторому диапазону. Тогда величина возбуждения превратится в булеву переменную, фиксируя событие.
Однако более универсальный подход основан на связывании величины возбуждения рецептора с достоверностью - вероятностью того, что величина скорости принадлежит одному или нескольким диапазонам. Такой подход мы и намерены воплотить в дальнейшем.
А именно, хотя бы интуитивно (а интуиция основана на опыте) определим достоверность того, что интересующая нас величина принадлежит данному диапазону. С какой достоверностью она принадлежит второму диапазону? А третьему?
Здесь явно просматривается концепция нечетких множеств [30].
Множество называется нечетким, если элементы входят в него с некоторой вероятностью.
Но можно даже уйти от понятия достоверности как вероятностной категории. Все ли мы знакомы с понятием исчерпывающего множества событий, связанным с условием нормировки, т.е. с условием равенства единице суммы их вероятностей? Ведь часто можно услышать: "Даю голову на отсечение, что это так, хотя и допускаю, что все наоборот…" Главное, чтобы исходные оценки информации были относительными, отражающими принцип "больше - меньше". Это расширит популярность нейротехнологий, исключит необходимость специальных знаний. Ведь какие-то начальные возбуждения рецепторов, при их относительном различии, распространятся по нейросети, определяя предпочтительность принимаемого решения!
Тогда, на этапе обучения нейросети, получим возможность формирования аналога некой таблицы, в соответствии с которой будет действовать инспектор. (Однако здесь пока не рассматривается процесс обучения нейросети - формирование этой таблицы, - а только принцип формирования данных для входа в нее.)
Выделим нейроны, "отвечающие" за типы автомобилей: отечественного производства, "мерседес", "вольво", "джип" и т.д. Величину возбуждения этих нейронов будем полагать равной 1 - на этапе обучения, или равной достоверности события - в рабочем режиме. Аналогично выделим рецепторы, "отвечающие" за другие возможные события: степень интеллигентности водителя (так же по диапазонам изменения), выигрыш или проигрыш любимой команды и т.д.
Следовательно, на входном слое будут формироваться приведенные значения возбуждения.
В рабочем режиме мы, таким образом, получили возможность использования неопределенной, недостоверной информации.Например, инспектор не смог из-за высокой скорости отличить "ниву" от "чероки". Тогда он решает ввести значение 0,5 в графу "нива" (величина возбуждения рецептора, "отвечающего" за "ниву", станет равной 0,5) и 0,5 - в графу "джип-чероки" (такой же станет величина возбуждения соответствующего рецептора). Однако, подумав, он на всякий случай вводит величину 0,2 в графу ВАЗ 2104, что также во власти его сомнений. Так же инспектор поступает и с другими характеристиками сложившейся ситуации в поисках наиболее достоверного решения по принципу наибольшей похожести.
Алгоритм трассировки нейросети
В результате решения примера сформировались и даже стали привычными действия, на основе которых мы можем сформулировать
Алгоритм трассировки (обучения по обобщенным эталонам) нейросети
Дополняем матрицу следования S транзитивными связями по алгоритму, представленному в разделе 3.4.Все нейроны выходного слоя не должны иметь в соответствующих им строках "пустых" элементов в позициях, соответствующих нейронам входного слоя. Пустой элемент указывает на отсутствие пути возбуждения от соответствующего нейрона входного слоя. Мы будем считать нейросеть построенной некорректно и нуждающейся во внесении дополнительных связей, например, непосредственно от нейрона входного слоя к нейрону выходного слоя.Организуем перебор всех обобщенных эталонных ситуаций и соответствующих им решений, последовательно закрепляя нейроны выходного слоя Выхi за обобщенными ситуациями. Для каждой обобщенной ситуации выполняем пункты 4-15.Для обобщенного эталона i (i = 1, 2, …, m) строим матрицу следования Si[Vi1, Vi2, …, Vir

Примечание. Так как в процессе такого вычеркивания могут образовываться новые подобные строки, а матрица S - треугольная, то это вычеркивание должно быть произведено последовательно, сверху вниз по одной строке. Тогда все вычеркивание выполнится за один проход. В противном случае, если сразу наметить для вычеркивания несколько строк (и столбцов), не избежать повторного, возможно, многократного анализа появления новых строк для вычеркивания.
Присваиваем признак "возбужден" всем нейронам входного слоя, представленным в матрице Si.Проверяем: содержит ли матрица Si более одной строки? Если содержит, выполняется следующий пункт, в противном случае выполняется пункт 3.Исключаем из матрицы Si строки и столбцы, соответствующие нейронам–входам, не обладающим признаком "возбужден".Выделяем множество столбцов матрицы Si, обладающих признаком "возбужден".
Выполняем действие, отраженное в пункте 5 (во внешнем цикле): исключаем из текущего вида матрицы Si строки (и столбцы), которые содержат количество единичных элементов меньшее, чем указанное при строке значение m.
Примечание. Такое действие необходимо после каждого вычеркивания строк и столбцов.
В совокупности выделенных столбцов находим (если таковая имеется) первую строку, содержащую максимальное число единиц и не содержащую единиц в других столбцах. (Число найденных единиц не должно быть меньше соответствующего значения m.) Соответствующий ей нейрон может быть переиспользован. Если такой строки найти не удается, выполняем пункт 13.
Исключаем из рассмотрения нейроны (вычеркиваем строки и столбцы) которым соответствуют единицы в найденной строке. Присваиваем нейрону, соответствующему выделенной строке, признак "возбужден". Уничтожаем в выделенной строке все нули и символы транзитивных связей, если они имеются, - превращаем строку во вход матрицы Si.
Примечание. В рассмотренном примере обращение строки во вход матрицы пришлось делать однажды, при трассировке третьего эталона. Однако при развитии примера в следующей лекции такое действие придется выполнять многократно.
Переходим к выполнению пункта 7.
В совокупности выделенных столбцов находим, если таковая имеется, первую строку, содержащую максимальное число нулевых элементов. Если такой строки найти не удается, выполняем пункт 15.
Меняем значение возбуждения соответствующих связей, то есть заменяем нули единицами. Присваиваем нейрону, соответствующему выделенной строке, значение m, равное количеству единиц в строке, и признак "возбужден". Исключаем из рассмотрения нейроны (вычеркиванием строк и столбцов), "передавшие" свое возбуждение найденному нейрону.
Примечание. Значения весов связей одного нейрона могут корректироваться лишь однажды. В других ситуациях, при обучении другим эталонам, нейрон может только переиспользоваться, если в этом обучении участвуют все те нейроны, возбуждение которых он использует с весом, равным единице.
При этом достаточно учитывать лишь число единиц в строке. В процессе такого обучения эталоны не мешают друг другу!
Внесенные изменения весов учитываем в матрице S. Переходим к выполнению пункта 7.
По каждому выделенному столбцу "спускаемся" вниз и находим первый из непустых элементов, соответствующий транзитивной связи. Вводим в нейросеть дополнительную связь, присваивая единичное значение найденному элементу. Исключаем из рассмотрения (вычеркиваем строки и столбцы) нейроны, соответствующие обработанным столбцам. Отражаем внесенные изменения в матрице S.
Примечание. Как мы видели в примере, а, по-видимому, это верно всегда, такая транзитивная связь потребуется на последней стадии выполнения алгоритма и может обнаружиться лишь в строке, соответствующей нейрону выходного слоя. Поэтому формировать значение m уже излишне, так как это может быть последним актом выполнения данного алгоритма.
Переходим к выполнению шага 7.
Описание алгоритма закончено.
Построенный алгоритм трассировки, несомненно, эвристический, то есть дающий приблизительное, удовлетворительное решение. Точный алгоритм трассировки, минимизирующий число использованных нейронов и дополнительных связей, требует совместного анализа всех эталонов и решений, выделения и создания термов, участвующих в получении всех решений. Но само понятие точности алгоритма трассировки проблематично ввиду неопределенности критерия.
Так, в нашем случае удачно сложился терм в результате связи [C1, C2, C3, C4,C5

Мы предлагаем читателю самому произвести трассировку сети, представленной на рис. 2.14, по предложенному алгоритму. Избежит ли он введения дополнительных связей? Мы не знаем. Но, во-первых, мы строим простой, нетрудоемкий алгоритм; во-вторых - мы же раньше говорили о нецелесообразности экономии! При такой скудости наших знаний на что нам тратить сто миллиардов нейронов с десятью тысячами дендритов каждый?!
опыт - предпосылки обобщения
Объединим множество эталонов, требующих возбуждения одного нейрона выходного слоя, понятием "обобщенный эталон". Например, эталоны А1

















Выберем нейросеть, отражающую, как нам кажется, все особенности, которые необходимо учесть при построении алгоритма трассировки, и, как мы уже начали, возьмем тот же пример, который выглядит теперь следующим образом:
 |
(4.1) |
Мы хотим, задавая обобщенный эталон на входе, например из тех, что приведены выше, экономным путем построить, возможно, пересекающиеся пути возбуждения, ведущие от каждого возбужденного входного нейрона в соответствующий нейрон выходного слоя. Способ должен быть экономным в том смысле, что пути должны быть максимально объединены, совмещены, реализуя стратегию слияния и выхода на общую, единую дорогу, ведущую к заветной цели.
При этом мы строим эвристический алгоритм, который крайне экономно расходует ресурсы сети - ее нейроны и связи, но и так же экономно вводит изменения, развивает сеть, если связей оказывается недостаточно.
Ибо мы видели, с каким трудом удается приспособить "готовую" нейросеть под конкретную задачу. Мы постоянно склонялись к вопросу: "А не лучше ли сразу строить сеть "под задачу", а не наоборот?" Нам кажется, мы нашли диалектический компромисс: беря что-то близкое, подходящее, мы минимально переделываем, словно костюм с жмущим гульфиком, купленный в универсальном магазине. Кроме того, нам очень важно сделать алгоритм доступным широким массам студенческой молодежи, овладевшей основами таинства параллельного программирования!

Рис. 4.1. Нейросеть, подлежащая обучению

Рис. 4.2. Матрица следования с транзитивными связями
Пусть выбранная нейросеть представлена на рис. 4.1, где первоначально заданные связи обозначены тонкими стрелками.
Строим соответствующую матрицу следования S и в ней - транзитивные связи (рис. 4.2). Проверяем, все ли нейроны выходного слоя достижимы из любого нейрона входного слоя. Если нет, считаем, что сеть составлена не корректно.
В данном случае из нейрона В1 не исходит ни одной статической цепочки, заканчивающейся нейроном Вых5. Это следует из того, что в строке, соответствующей нейрону Вых5, нет даже транзитивной связи в столбце, соответствующем нейрону В1. То же касается нейрона В3.
Введем синапсические связи В1


Сформируем статический путь возбуждения {B1, A1, C1, C2, C3, C4, C5}



Рис. 4.3. Матрица следования при обучении первому эталону
Пытаясь сымитировать прокладываемые пути возбуждений, снабдим все нейроны входного слоя, отраженные в этой матрице, признаком "возбужден".
Такая строка соответствует нейрону 11. Заменяем в этой строке (в выделенной совокупности столбцов) "нули" "единицами", т.е. максимально увеличиваем веса. Присваиваем нейрону 11 признак "возбужден" и значение m11 = 3. Отражаем изменение весов в матрице S.
Исключаем из матрицы S1 строки и столбцы, соответствующие нейронам В1, А1, 6. Матрица принимает вид, изображенный на рис. 4.5.

Рис. 4.5. Шаг преобразования матрицы следования
Исключаем из матрицы все входы, которые соответствуют нейронам 1, 2, 3, 4, 5, не обладающим признаком "возбужден". Ведь строящийся нами путь возбуждения уже миновал эти нейроны! Исключение этих нейронов породит новые нейроны, нуждающиеся в исключении по той же причине, - нейроны 9 и 10.
Последовательное исключение сверху вниз динамически учитывает появление таких нейронов и гарантирует полное исключение за один проход. Матрица S1 примет вид на рис. 4.6.

Рис. 4.6. Шаг преобразования матрицы следования
Теперь в первом столбце имеется единственная строка с "нулем" - соответствующая нейрону Вых1. Меняем "нуль" на "единицу" - получаем окончательный возможный динамический путь возбуждения по заданному эталону. Изменения отражаем в матрице S.
Мы не будем приводить новый вид матрицы следования S, а на изображении самой сети (рис. 4.7) выделим темным построенную трассу (она же - опорный путь, а также динамический путь возбуждения по предлагаемому эталону).
Реакции на эталон одной комбинации мы сеть научили.
Составим обобщенный эталон ситуации, требующий решения R2, - {A1, B2, B3, C1, C2, C3}. Свяжем это решение с нейроном Вых2.
По сети на рис. 4.7 или по матрице на рис. 4.2 (с учетом частичного обучения!) построим (рис. 4.8) матрицу статического пути возбуждения S2[B2, B3, A1, C1, C2, C3

Нейрон 6 ранее "объединил" возбуждение пяти нейронов: С1, С2, С3, С4, С5, т.е. в матрице S в соответствующей строке содержится пять единиц и m6 = 5. Однако в составленной матрице S2 в строке, соответствующей этому нейрону, присутствуют лишь три единицы.
Значит, этот нейрон не может быть использован для трассировки необходимого пути возбуждения, т.к. комбинация С1&С2&С3&С4&С5 нам здесь не нужна.

Рис. 4.7. Нейросеть, обученная первому эталону

Рис. 4.8. Матрица следования для обучения второму эталону
То же следует сказать и о нейроне 11.
Исключим из данной матрицы строки и столбцы, соответствующие нейронам 6 и 11. Матрица примет вид, показанный на рис. 4.9.

Рис. 4.9. Шаг преобразования матрицы следования
Объединяем столбцы множества входов матрицы, обладающих признаком "возбужден". На данном шаге - это первые шесть столбцов матрицы. Находим в них первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 4. Меняем в ней все нули на единицы, полагаем m4 = 4. Присваиваем нейрону 4 признак "возбужден". Отражаем внесенные изменения весов в матрице S.
Исключаем из матрицы S2 строки и столбцы, соответствующие нейронам В2, А1, С1, С2, "передавшим" свое возбуждение нейрону 4.
Вновь объединяем столбцы множества входов, обладающих признаком "возбужден". Это столбцы, соответствующие нейронам В3, С3, 4. В совокупности этих столбцов выбираем первую из строк, содержащую максимальное число нулей. В данном случае это строка, соответствующая нейрону 1. Меняем нуль на единицу, полагаем m1 = 1, нейрону 1 присваиваем признак "возбужден".
Исключаем из матрицы строку и столбец, соответствующие нейрону В3, "передавшему" возбуждение нейрону 1. Исключаем из матрицы строки и столбцы, соответствующие образовавшимся входам - "не возбужденным" нейронам 2 и 3.
Выделяем столбцы, которые соответствуют нейронам - входам, обладающим признаком "возбужден", и в их совокупности находим строку, обладающую наибольшим числом нулей. Такая строка соответствует нейрону 10. Меняем нули на единицы, присваиваем нейрону признак "возбужден", полагаем m10 = 2.
Исключаем из матрицы S2 строки и столбцы, которые соответствуют нейронам 1 и 4, передавшим возбуждение нейрону 10.
Нейрон 9, не обладающий признаком "возбужден", образует вход матрицы. Исключаем соответствующие ему строку и столбец.
Выделяем столбцы, соответствующие нейронам С3 и 10, и в них находим строку с максимальным числом нулей. Первая из таких строк соответствует нейрону 5. Заменяем в ней единственный нуль единицей, присваиваем нейрону признак "возбужден", полагаем m5 = 1. Отражаем изменение веса в матрице S.
Исключаем из матрицы S2 строку и столбец, которые соответствуют нейрону С3, передавшему возбуждение нейрону 5.
Исключаем строку и столбец, соответствующие нейрону 7, как порождающему вход матрицы и не имеющему признака "возбужден".
В совокупности выделенных столбцов, соответствующих нейронам 5 и 10, строка, соответствующая нейрону 12, имеет единственный нуль. Меняем его на единицу, присваиваем нейрону 12 признак "возбужден", полагаем m12 = 1. Отражаем внесенное изменение веса в матрице S. Исключаем из матрицы S1 строку и столбец, соответствующие нейрону 5.
И, наконец, на последнем шаге, заменяя нули в строке, соответствующей нейрону Вых2, единицами, мы получим окончательный искомый путь возбуждения. Отразим его на рис. 4.10 нейросети.

Рис. 4.10. Нейросеть после обучения двум эталонам
Обучим сеть третьей ситуации, требующей решения R3. Закрепим за этим решением нейрон Вых3. Матрица S3[B2, B3, A1, C4, C5


Рис. 4.11. Матрица следования для обучения третьему эталону
Исключаем из матрицы S3 представительство тех ранее использованных ("возбужденных") нейронов, для которых значение m (указано в дополнительном столбце матрицы) превышает количество единиц в соответствующей строке. Это значит, что эти нейроны "собрали" уже возбуждение нейронов, которые в данном пути возбуждения, т.е. в матрице S3, не используются. Это нейроны 4, 5, 6, 11. Переиспользование их невозможно.
Повторяем попытки исключения из матрицы S3 представительства тех нейронов, для которых значение m стало превышать количество единиц в соответствующей строке.
И так далее - до исчерпания этой возможности.
В данном случае нам придется исключить из рассмотрения (вследствие исключения нейронов 4 и 5) нейроны 10 и 12. Матрица S3 примет окончательный вид на рис. 4.12.

Рис. 4.12. Шаг преобразования матрицы следования
Присваиваем всем нейронам, образующим входы матрицы, признак "возбужден".
Выделяем и объединяем столбцы, соответствующие входам матрицы S3.
Разовьем предшествующие аналогичные действия следующим образом.
В выделенных столбцах находим строку, содержащую хотя бы одну единицу. Она (строка) представляет тот нейрон, который "собрал" (при анализе предыдущих эталонов) возбуждение одного или более нейронов, образующих входы. Эти нейроны, "передавшие" свое возбуждение, могут быть исключены из рассмотрения. Среди таких строк выбираем строку с максимальным числом единиц.
Так, нейрон 1 возбужден единственным нейроном, принадлежащим текущему множеству входов матрицы, - нейроном В3. Впредь он представляет этот нейрон, который может быть исключен из рассмотрения. Матрица S3 принимает вид на рис. 4.13.

Рис. 4.13. Шаг преобразования матрицы следования
Подтверждаем нейрону 1 признак "возбужден" и превращаем его во вход матрицы S3, уничтожив веса в его строке.
Вновь находим множество входов матрицы и выделяем соответствующие им столбцы. Пытаемся найти строку, содержащую единицы в этих и только этих столбцах, но таких больше нет. Тогда находим строку, содержащую максимальное число нулей. Первая такая строка соответствует нейрону 2. "Объединяем" на нем возбуждение нейронов В2 и А1, заменяя нули единицами. Полагаем m2 = 2, исключаем нейроны В2 и А1 из рассмотрения, присваиваем нейрону 2 признак "возбужден". Отражаем сделанные изменения весов в матрице S.
Исключаем входы, не обладающие признаком "возбужден", - нейроны 3 и 5.
Выделяем столбцы, соответствующие входам. В их совокупности не находим строк, содержащих единицы. Тогда находим строку, содержащую максимальное число нулей.
Такая строка соответствует нейрону 7. Меняем нули (в выделенной совокупности столбцов!) на единицы, полагаем m7 = 2, присваиваем нейрону 7 признак "возбужден", отражаем изменение весов в матрице S. Исключаем нейроны С4 и С5 из рассмотрения. Сразу замечаем, что сформируется "невозбужденный" вход, соответствующий нейрону 8. Исключаем из рассмотрения и этот нейрон (рис. 4.14).

Рис. 4.14. Шаг преобразования матрицы следования
Выделяем столбцы, соответствующие "возбужденным" входам, и не находим строк, содержащих единицы. Тогда находим первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 13. Меняем нуль на единицу, нейрону 13 присваиваем признак "возбужден", полагаем m13 = 1. Исключаем нейрон 7 из рассмотрения.
Выделяем столбцы, соответствующие множеству "возбужденных" входов. В них не находим строку с единицами, но единственная строка с максимальным числом нулей соответствует нейрону Вых3. Меняем нуль на единицу. Однако статус этого нейрона особый, и значение m, как и признак "возбужден", ему не присваиваем.
Исключаем нейрон 13 из рассмотрения.
Выделяем множество столбцов, соответствующих "возбужденным" входам. Это столбцы, соответствующие нейронам 1 и 2. Пытаемся в этих столбцах найти строку с единицами, затем с максимальным числом нулей, - но таковых нет! Значит, необходимо введение дополнительных связей. Тогда в каждом столбце при просмотре сверху вниз находим первую транзитивную связь и меняем ее на единицу. Это означает, что данная сеть дополняется динамическими цепочками возбуждения 1


Построение трассы решения R3 закончено. После этого этапа обучения сеть имеет вид как на рис. 4.15.
Приступим к обучению следующему обобщенному эталону - решению A2&B3&C1&C2&C3&C4&C5


Исключим из рассмотрения те нейроны, для которых количество единиц в строках меньше значения m. Такими нейронами являются 4 и 11. Матрица S4 имеет вид как на рис. 4.17.

Рис. 4.15. Нейросеть после обучения третьему эталону

Рис. 4.16. Матрица следования для обучения четвертому эталону

Рис. 4.17. Шаг преобразования матрицы следования
Присваиваем всем нейронам-входам значение "возбужден". Выделяем столбцы, соответствующие входам - первым строкам "возбужденных" нейронов. Это первые семь столбцов. Среди строк этой совокупности столбцов находим строку с максимальным числом единиц в этих столбцах, при отсутствии единиц в других столбцах. Это строка, соответствующая нейрону 6. Теперь нейрон 6 будет представлять нейроны С1, С2, С3, С4, С5, "передавшие" ему свое возбуждение. Присваиваем ему признак "возбужден", исключаем из рассмотрения перечисленные нейроны, матрица S4 принимает вид как на рис. 4.18.

Рис. 4.18. Шаг преобразования матрицы следования
Для "не возбужденных" нейронов исключаем из матрицы S4 строки (и столбцы), число единиц в которых стало меньше соответствующего значения m. Они соответствуют нейронам 5 и 7. Повторяем этот шаг до полного исключения таких нейронов, - исключаются нейроны 12 и 13. Матрица имеет вид как на рис. 4.19.

Рис. 4.19. Шаг преобразования матрицы следования
Исключаем из рассмотрения множество "невозбужденных" входов. К таким относится нейрон 8. Выделяем множество столбцов, соответствующих входам матрицы. В их совокупности находим первую строку, обладающую максимальным числом нулей (единиц нет во всей матрице!). Такая строка соответствует нейрону 3. Нули в ней соответствуют нейронам В3 и А2. Исключаем эти нейроны из рассмотрения, полагаем m3 = 2, присваиваем нейрону 3 признак "возбужден".
Вновь выделяем множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, находим строку с максимальным количеством нулей. Эта строка соответствует нейрону 14. Заменяем в ней нуль на единицу, полагаем m14 = 1, присваиваем нейрону 14 признак "возбужден".
Исключаем нейрон 6 из матрицы. Матрица принимает вид как на рис. 4.20.
Рис. 4.20. Шаг преобразования матрицы следования
Выделяем множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, находим строку с максимальным количеством нулей. Эта строка соответствует нейрону выходного слоя Вых4. Меняем в ней нуль на единицу. Так как это - нейрон выходного слоя, не присваиваем ему признак "возбужден" и значение m. Исключаем нейрон 14 из рассмотрения. Матрица имеет вид как на рис. 4.21.

Рис. 4.21. Шаг преобразования матрицы следования
В этой матрице множество "возбужденных" входов составляет единственный нейрон 3. Однако в его столбце нет ни единичных, ни нулевых элементов. Тогда, как и прежде, вводим в сеть дополнительную связь, найдя в столбце, соответствующем нейрону 3, первую сверху транзитивную связь и положив ее вес равным единице. Эта связь порождает динамический путь возбуждения 3

Построение трассы решения R4 закончено. Не приводя промежуточного вида матрицы S, дадим на рис. 4.22 вид сети, полученной после данного этапа трассировки.
И, наконец, приступим к трассировке последнего пути возбуждения. Он осуществляется по обобщенному эталону, требующему решения R5, A2&B1&B2&C1&C2&C3&C4&C5

На основе текущего вида матрицы S построим матрицу S5[B1, B2, A2, C1, C2, C3, C4, C5


Рис. 4.22. Нейросеть после обучения четырем эталонам

Рис. 4.23. Матрица следования для обучения пятому эталону
Присваиваем всем входам признак "возбужден".
Выделяем столбцы, соответствующие "возбужденным" входам. В совокупности этих столбцов находим строку, содержащую максимальное число единиц в этих и только этих столбцах, если таковые имеются. В данном случае это строка, соответствующая нейрону 6. Присваиваем нейрону 6 признак "возбужден" и исключаем из рассмотрения нейроны С1, …, С5.
Исключаем из рассмотрения нейроны 5 и 7, так как в соответствующих им строках отсутствуют единицы при отличных от нуля значениях m. Однако видно, что после их исключения придется исключить по той же причине нейроны 12 и 13. Получившаяся матрица представлена на рис. 4.24.

Рис. 4.24. Шаг преобразования матрицы следования
Исключаем из рассмотрения "невозбужденный" вход, соответствующий нейрону 8. Выделяем столбцы, соответствующие "возбужденным" входам, и в их совокупности находим строку, содержащую наибольшее число единиц при отсутствии единиц в других столбцах. Такая строка соответствует нейрону 14. Исключаем из рассмотрения нейрон 6 как передавший свое возбуждение нейрону 14, присваиваем нейрону 14 признак "возбужден". Матрица S5 принимает вид как на рис. 4.25.

Рис. 4.25. Шаг преобразования матрицы следования
Выделяем столбцы входов, соответствующие "возбужденным" нейронам, и в их совокупности находим строку, содержащую максимальное число нулей (строк с единицами больше нет). Такая строка соответствует нейрону выходного слоя Вых5. Меняем нули на единицы. Исключаем нейроны В1 и 14 из рассмотрения. Отражаем введенные изменения в матрице S. Новый вид матрицы S5 приведен на рис. 4.26.

Рис. 4.26. Шаг преобразования матрицы следования
Выделяем множество столбцов, соответствующих входам матрицы. В этих столбцах не находим ни строк, содержащих единицы, ни строк, содержащих нули. Тогда в каждом столбце заносим единицы на места транзитивных связей, то есть вводим связи В2


Трассировка (обучение сети по обобщенным эталонам) закончена. Окончательный ее вид представлен на рис. 4.27, где, напоминаем, веса, принявшие значение 1, соответствуют жирным стрелкам.

Рис. 4.27. Обученная нейросеть
Приведение нейросети после трассировки
Зафиксируем передаточную функцию, например

Будем задавать конкретные эталоны и наблюдать величину возбуждения соответствующего нейрона выходного слоя.
Рассмотренный выше пример нехарактерен. В нем каждый эталон приводил, при данной передаточной функции, к одинаковой величине возбуждения нейронов выходного слоя. Но, например, при распознавании знаков алфавита величины возбуждения нейронов выходного слоя, в ответ на предъявление различных эталонов, могут быть различными. Так, в первом примере лекции 2 для записи буквы О потребовалось возбуждение шести нейронов-рецепторов, а для записи буквы А – восьми рецепторов. Очевидно, эталон латинской I "засветит" на входном слое (на клетчатке) меньшее число нейронов, чем, скажем, буква Q, но значительно большее число, чем необходимо для записи запятой. Значит, при рассматриваемых простейших видах передаточной функции величины возбуждения на выходе будут существенно различаться.
Тогда закрадывается подозрение: а не приведет ли некоторое незначительное искажение ситуации А, логично требующее все же решения RA, в сторону ситуации В, то есть принятия решения RB?
Разная по возможному максимуму величина возбуждения нейронов выходного слоя утверждает неравноправие, приоритет ситуаций. И возбуждение нейронов выходного слоя следует как-то уровнять по эталонным ситуациям, привести к одному диапазону изменения или к достаточно близким величинам.
Введем эту величину U, например, как максимальное значение возбуждения некоторого нейрона выходного слоя или понравившуюся нам оценку, не обязательно превышающую такой максимум. Введем для каждого нейрона выходного слоя коэффициент приведения

Однако значение Vj находим не по обобщенному эталону, а по каждой конкретной ситуации, входящей в состав обобщенного эталона. Например, ситуация {A1, B1, C1} образует реальный эталон в составе обобщенного эталона {A1, B1, C1, C2, C3, C4, C5}. По нему (другие ситуации аналогичны) находится величина возбуждения VВых1 нейрона Вых1. Значит,

Впредь, в режиме распознавания, каждое значение возбуждения нейрона выходного слоя будем умножать на его коэффициент приведения. Таким образом, мы поставим все ситуации на входе в равное положение.
Однако в лекциях 9–11 будет показано, что в общем случае проблема приведения значительно более сложна. Она требует корректировки весов связей, в частности, в зависимости от того, какая логическая операция явилась прообразом данного нейрона выходного слоя.
Динамизм обучения
На самом деле обучение не бывает внезапным, как мы это представили выше, рассматривая сразу обобщенные эталоны. Мгновенное заполнение губки памяти нашего разума из Всеобщего Информационного Пространства в момент рождения - лишь фантастическая мечта, которая опирается на опыт предшествующих земных цивилизаций, известный восточным учениям. Долгий и тернистый путь образования (слово-то какое в русском языке: образование - создание, произведение, построение, - человека!), предполагает многократность и постепенность, изменяемость в совершенствовании и утверждение, трудоголический надрыв и преодоление, победный клич и разочарование.
Итак, можно учить по "чистым" эталонам, объединив их в эталоны обобщенные. Но "ближе к жизни" можно учить по разным "частным" эталонам (то, что мы называем жизненным опытом), приводящим к одному решению. Например, можно (возвращаясь к многострадальному примеру) последовательно "показывать" эталоны B1&A1&C2, B1&A1&C1 и т.д., приводящие к решению R1. Можно предъявлять вперемежку разные эталоны, приводящие к разным решениям. И это справедливо соответствует диалектике познания на основе гипотез, экспериментов и опыта, гласящей, что мир познаваем, но всего познать нельзя, ибо, мы добавляем, - Бесконечность!
Например, дядя Рамзай не мог ранее предвидеть некоторых комбинаций событий, предварительно имея ошибочное суждение о распределении работ своих клиентов. Или ему даже пришлось употребить свои связи для того, чтобы осуществить вожделенную мечту: включить в орбиту своих действий восхитительную многоприбыльную продукцию фирмы Ночная Бабочка!
Во всех случаях на этапе обучения целесообразно определять события А, В, С с максимальной достоверностью, равной единице, рассчитывая тем самым реакцию нейросети на вполне определенные ситуации. Это следует из того, что даже возникшая при предъявлении эталона малая величина возбуждения нейрона входного слоя указывает, что событие возможно и, следовательно, нуждается в рассмотрении.
Интуиция же нам подсказывает, что надо действовать как-то проще, тем более что мы не постесняемся ввести дополнительные связи в сеть, если понадобится.
Итак, рассмотрим проблему динамического включения новых частных эталонов в состав обобщенного эталона на фоне уже произведенного частичного обучения нейросети.
Пусть предъявление эталонов A1&B1&C2 и A1&B1&C4 ("текущий" обобщенный эталон A1&B1&C2&C4), требующих решения R1, а также предъявление текущих обобщенных эталонов A1&B2&C1&C2&C3, A1&B2&C4&C5, A2&B3&C1&C2&C3&C4&C5, A2&B1&C1&C2&C3&C4&C5, требующих соответственно решений R2, R3, R4, R5, привели к трассировке нейросети (к ее текущему состоянию), представленной на рис. 5.1.

Рис. 5.1. Частично обученная нейронная сеть
Здесь "жирные" связи обладают максимальным значением веса (скорее всего - единичным). Такое состояние получено с помощью алгоритма трассировки, представленного в предыдущей лекции, и это предлагается проверить читателю в порядке закрепления материала.
Матрица следования S, соответствующая получившейся сети, показана на рис. 5.2.

Рис. 5.2. Матрица следования
Как видим, сеть оказалась весьма "запутанной" дополнительными связями. Обучение всем обобщенным эталонам сразу (пример в лекции 4) выявляет термы, использующиеся при получении различных решений. Здесь же термы не складывались, нейроны почти не переиспользовались.
Это и привело к формированию большого числа дополнительных связей. (Мы не любим, когда из нас "вытягивают" одно за другим. Мы возмущаемся: "Не тяни, выкладывай все, что тебе нужно!")
То есть нам необходимо построить путь возбуждения (трассы) B1, A1, C1, C2, C3, C4


Значит, надо проложить трассы, дополнить сеть путем возбуждения C1, C3

Преследуя эту цель, мы не должны допустить слияния, влияния этого пути на пути возбуждения, ведущие в другие нейроны выходного слоя. Такая опасность кроется в естественном желании переиспользования нейронов. Ведь слияние двух путей возбуждения заключается в том, что у некоторых нейронов следует повысить веса синапсических связей (скажем, положить равным единице, вместо нуля, окрасить в красный цвет). То есть некоторые нейроны могут стать преемниками возбуждения большего, чем прежде, числа нейронов. А если эти нейроны использовались для получения других решений?
Здесь важно сделать Замечание в дополнение к алгоритму трассировки, рассмотренному в лекции 4:
целесообразно при переиспользовании нейронов, возникающем при последовательном анализе обобщенных эталонов , фиксировать информацию: участвует ли данный нейрон лишь в одном пути возбуждения - к единственному нейрону выходного слоя и к какому именно, или к более чем к одному нейрону выходного слоя. И этого будет вполне достаточно для ликвидации тревог.
Продолжим рассмотрение примера, ведущее к обобщению.
Для нового обобщенного эталона на основе матрицы S, так же, как мы это делали в предыдущем разделе, построим (рис. 5.3) матрицу S*[B1, A1, C1, C2, C3, C4

В соответствии с правилом ее построения в ней представлены лишь те нейроны, для которых число единиц в строке равно соответствующему значению m. Для каждой строки, содержащей единичные элементы, указано, используется ли нейрон для получения единственного решения и какого (признак Выхi), или не единственного (признак отсутствует).

Рис. 5.3. Матрица следования для обучения уточненному эталону
Исключим из построенной матрицы строки и столбцы, соответствующие нейронам, участвующим в путях возбуждения, не ведущих в Вых1 (рис. 5.4). (В общем случае в матрице могли сохраниться строки, содержащие нулевые веса.)

Рис. 5.4. Шаг преобразования матрицы следования
"Спускаемся" по столбцу, соответствующему нейрону С1, и в строке, не являющейся входом, находим, если таковой имеется, первый нулевой элемент. Полагаем его равным единице и отражаем введенное изменение в матрице S. Если нулевого элемента в столбце не нашлось, находим первый "пустой" элемент (или отмеченный транзитивной связью - все равно) и полагаем его равным единице. Этим мы вводим дополнительную связь, отраженную в матрице S. В данном случае такой связью с единичным весом является связь С1

То же проделываем с нейроном С3, введя дополнительную связь с единичным весом С3


Рис. 5.5. Шаг преобразования матрицы следования
Отметим, что наше решение основано на эвристике, и место появления новых возбужденных связей может быть оспорено. Например, могли быть построены связи С1






Мы не приводим еще более усложнившегося рис. 5.1 уточненной сети, предоставив читателю возможность проверить усвоение материала с помощью легкого нажатия красным карандашом прямо в книжке в направлении стрелок, которые исходят из кружочков, помеченных символами С1 и С3, и входят в кружок, помеченный цифрой 2. Однако намек на такое уточнение делаем на рис. 5.6.

Рис. 5.6. Полностью обученная нейросеть (намек)
Не задавайте глупых вопросов!
"Родила царица в ночь
Не то сына, не то дочь…"
А.С. Пушкин
Мы учим сеть по обобщенным эталонам, несомненно опираясь на здравомыслие пользователя. Так, обучая обобщенному эталону A1&B2&B3&C1&C2&C3, мы предполагаем задание "логичных" вопросов типа: "Какое решение принять, если Вася на своем прекрасном "Volvo" отправился в павильон "Роксана", в который накануне завезена из Китая большая партия косметики?". Вы задаете сети ясный вопрос, полагая А1 = В3 = С2 = 1 (на самом деле вы знаете об истинном происхождении косметики), и получаете столь же ясный ответ: "Принимай решение (или значение твоей прибыли) R2!"
Но что, если при сформировавшихся связях задать вопрос В3 = С1 = С2 = С3 = 1? Максимального и равного возбуждения на выходе достигнет даже не один нейрон! Но что означал этот вопрос и что означал ответ? Судить ли по неоднозначности ответа о том, что на входе сформировано "объединение" вопросов, обусловившее неоднозначность ответов? (Каков вопрос - таков ответ?) А всегда ли получается неоднозначный ответ?
Зададим вопрос, положив А2 = В1 = В2 = 1. Максимального возбуждения достигнет нейрон Вых5. Но предусматривалось ли решение R5 в ответ на такую ситуацию? Хотя завоз продукции фирм Красный киллер и Пират в палатки С1, С2 и С3 накануне визита Пети вполне возможен!
Несомненно, для правильного ответа надо правильно ставить вопрос. Корректность использования нейросети должна быть обусловлена теми правилами, которые брались за основу ее разработки. Если мы положили, что события А, В, С обязательно должны участвовать в формировании вопросов, то для задания других вопросов сеть необходимо дополнительно обучить.
Например, вопрос "Фирма В3 направила свою продукцию в палатки С1, С2 и С3, - что делать?" требует тщательной проработки нового ответа R6 на свободном нейроне Вых6 выходного слоя и формирования (трассировки) пути возбуждения В3, С1, С2, С3

Однако возможности неоднозначного ответа (одинаковой величины возбуждения нейронов выходного слоя) этим избежать не удается.
Придется анализировать всю картину возбуждения нейронов выходного слоя и выдавать все ответы вида: "Продукция фирмы В3 поступила в палатки С1, С2, С3"; "Это впоследствии, скорее всего, приведет к решениям R2 и R4". А это, нетрудно видеть, влечет необходимость надстройки сети вторым логическим уровнем, где выходной слой нейронов первого уровня становится (возможно, в совокупности со своим входным слоем) входным слоем. Так могут быть продолжены логические цепочки наших умозаключений.
Это еще раз свидетельствует о том, что нельзя законсервировать себя как носителя нейросети на всю жизнь, получив стандартный объем знаний, удостоверенный "красным" дипломом. Надо думать, надо учиться, надо развиваться, смело задавая "запрещенные", глупые вопросы…
***
Как показал исторический опыт, демократия и гласность без запретов кроме вреда ничего не приносят. Или это не так? Или именно запрещенные вопросы милы Развитию? Рассмотрим это подробнее ниже.
Познание нового - основа самообучения
"Кто стрелял, куда попал?"
А. Твардовский, "Василий Теркин"
Конечно, вы сами можете открыть квантовую механику. Но лучше спросить "Что это такое?" за кружкой пива у бедного студента, подрабатывающего грузчиком в соседнем гастрономе.
Мы научили сеть множеству эталонов - даже сформированных в обобщенные эталоны. Теперь, подавая на вход даже искаженные образы, мы можем ответить на вопрос "На какой эталон в большей мере он похож?". И максимально возбужденный нейрон ответит нам на него. Рассмотрим, однако, более внимательно пороги, которым мы уделяли недостаточное внимание.
Что если, более серьезно отнесясь к порогам, установить ограничение на величину возбуждения нейрона выходного слоя, столь решительно дающего определенный ответ? А именно: если величина максимального возбуждения меньше порога H, следует считать, что сеть не знает, что за образ подан на ее вход, и вправе рассматривать его как новый эталон для обучения.
Тогда должен быть найден "свободный" нейрон выходного слоя, и по вышеприведенному алгоритму должна быть произведена трассировка.
Так производится запоминание эталона как некоторой диковинки. Для последующего использования новых знаний трудно обойтись без внешнего воздействия, без учителя, ибо неизбежен вопрос: "Что это и что из этого следует?". Мы знаем, насколько длителен путь эволюции, основанный на "чистом" самообучении, без воздействия, влияния, поддержки извне. Пример Маугли нас не вдохновляет.
Мы даже можем представить себе возможный диалог между Нейрокомпьютером (НК) и Учителем (У):
НК (Величина возбуждения ни одного нейрона выходного слоя не одолела порога):
- Это что-то новенькое! Повтори вопрос; может, величины возбуждения на входе малы?
У:
- Повторяю вопрос.
НК (Результат тот же):
- Все же это что-то новенькое. Приводит ли это к одному из известных решений, или решение новое?
У (Варианты):
- Это должно привести к решению R5.
- Это новое решение R6.
НК (Соответствующие варианты):
- Произвожу трассировку по уточненному обобщенному эталону для решения R5.
- Рассматриваю твой вопрос как новый обобщенный эталон. Произвожу трассировку к выходному нейрону Вых6, соответствующему решению R6.
(Пауза)
Здесь идет самообучение системы "Учитель - Нейрокомпьютер". Полное или близкое к нему самостоятельное обучение Нейрокомпьютера возможно тогда, когда сеть - многоуровневая, то есть одни выводы являются посылками для других. Оно возможно, если сеть знакома хотя бы с понятиями "хорошо" и "плохо", то есть учитывает критериальную функцию, так необходимую для моделирования. Это уже высшие сферы обучения, которые мы наблюдаем пока в природе и лишь экспериментально, но постепенно надеемся покорить на основе изложенных здесь предпосылок.
Мы уверены, что любая достаточно развитая нейросетевая система должна быть многоуровневой, допускающей цепочки выводов. Иначе трудно представить себе такие диалоговые системы, с помощью которых производится постепенное уточнение при успешном продвижении к Большой Правде.
Например, диалог при медицинской диагностике формируется, несомненно, на основе отработанной стратегии допроса. Предполагается, что вопросы структурированы и даже образуют порядок следования, отраженный графически, так, что одни вопросы исключают другие. Например, уместен ли вопрос "Снились ли вам гномики?" после отрицательного ответа на вопрос "Спали ли вы в эту ночь?" - при рецидивах недержания?
В то же время принцип нейросети обязан выручить тогда, когда вопросы нелогичны, несовместимы. Просто все нейроны выходного слоя не превысят порога, и НК вступит в диалог с Пользователем (П), подобный предыдущему. Если же ответ на логичный вопрос не был предусмотрен экспертами (Учителем), то этот недостаток должен быть устранен трассировкой нового решения.
Правда, новым решением - реакцией на этот вопрос - может быть ответ: "Не задавай глупых вопросов!"
В общем случае диалог Пользователя с Нейрокомпьютером может выглядеть следующим образом.
НК (Первый вопрос после входа):
- Что у вас болит?
П:
- Голова, живот, пальчик.
НК (После ввода и обработки сигналов - величин возбуждения нейронов входного слоя, соответствующих понятиям "голова", "живот", "левый указательный палец", максимально возбуждается нейрон промежуточного выходного слоя, инициирующий следующий вопрос):
- Ковыряли ли вы в носу на сон грядущий?
П:
- Да.
НК:
- Мыли ли вы руки, ложась спать?
П (Варианты):
- Я мою только ноги.- Нет.
НК (Варианты):
- Не задавайте глупых вопросов!
(На правах рекламы) - Не волнуйтесь, но вы страдаете манией величия. Вам срочно необходимо обратиться в Российский Пенсионный Фонд!
***
В этом месте остановись, читатель, и отрешенным взором обозначь ясную мысль: "Так может ли существо, называемое Божьей Тварью, жить и действовать одним лишь мозгом - нейросетью в механическом, бессознательном состоянии? Достаточен ли мозг в такой ограниченной интерпретации аппарата, инструмента, - для творчества и самопознания? Или все нами изложенное не достойно даже червячка? Есть ли в нас что-то выше такого мозга?" и т.д. и т.д.
Нет, не хочется чувствовать себя только думающей машиной! - И мы размашисто осеняем себя крестным знамением…
К вопросу происхождения человека
"…если бы человек, властитель мира, умнейшее из дыхательных существ, происходил от глупой и невежественной обезьяны, то у него был бы хвост и дикий голос. Если бы мы происходили от обезьян, то нас теперь водили по городам цыганы на показ и мы платили бы деньги за показ друг друга, танцуя по приказу цыгана или сидя за решеткой в зверинце… Разве мы любили бы и не презирали бы женщину, если от нее хоть немножко пахло бы обезьяной, которую мы каждый вторник видим у Предводителя Дворянства?"
А.П. Чехов. "Письмо к ученому соседу"
Тезисы "человек произошел от обезьяны" и "человек произошел не от обезьяны", в основе которых лежит обидная похожесть, по-видимому, одинаково неверны, ибо из закона отрицания отрицания следует, что правда лежит где-то посредине. Вероятно, два процесса успешно сосуществовали: один – в соответствии с непреложностью идеи Развития, другой – в соответствии с неотвратимостью внешнего цивилизованного воздействия.
В схоластической защите лишь одного из этих тезисов сказывается отсутствие обратной связи: влияния сделанного вывода на исходную посылку. Наличие обратной связи способно отвергнуть посылку, произвести доказательство "от противного" так, как это блестяще выполнил Василий Семи-Булатов.

Рис. 6.1. Нейросеть для решения вопроса о происхождении человека
Но не только сделанный вывод должен влиять на исходную посылку. На нее посылку должны влиять и другие выводы, в совокупности определяющие знания. (Ведь вспомнили же мы закон отрицания отрицания!) Обратные связи без знаний могут свести на нет весь блеск интеллекта и привести только лишь к показанному великим писателем каламбуру.
Попробуем построить проект, эскиз, набросок фрагмента нейросети, отражающей глубину умозаключений чеховского героя и дополненной доступными нам понятиями более высокого свойства (рис. 6.1).
При построении нейросети учитываем следующее.
Посылка "человек произошел от обезьяны" обязательно должна привести к абсурдному выводу "у человека есть хвост" (нейрон 6).
Тогда обязательно должна существовать отрицательная обратная связь , которая ведет к нейрону 1 входного слоя, "ответственному" за указанный тезис, и снижает заданную извне величину его возбуждения. Это значит, что этот нейрон должен получать возбуждение нейрона выходного слоя с помощью дендрита, обладающего отрицательным синапсическим весом. Отрицательная связь помечена на рисунке знаком "-".
Примечание. Ранее мы отличали нейроны-рецепторы входного слоя от других нейронов. Рецепторы возбуждались только извне. Теперь мы видим, что это такие же нейроны, как и все другие. Просто некоторые их дендриты получают возбуждение извне, а некоторые – от других нейронов сети.
Одновременно положительная обратная связь должна усиливать возбуждение нейронов 2 и 3, "ответственных" за тезисы о божественном и марсианском происхождении человека.
Такое же влияние на нейроны 1–3 должны оказывать и другие выводы, за которые "ответственны" нейроны 7–9.
Однако действенен и довод "То, что дурно пахнет, недостойно любви". Дурной запах давит, угнетает позывы любви, порождая отрицательную обратную связь – признак сомнений в происхождении человека.
На стрелках, обозначающих связи, указаны их веса ?, в том числе – отрицательные. Выбор весов обусловлен тем, что три события-высказывания, соответствующие нейронам 1–3, образуют исчерпывающее множество событий. Тогда, в соответствии с условием нормировки, уменьшение достоверности одного из них должно увеличивать достоверность других.
Выберем передаточную функцию

Выберем значения порогов равными нулю для нейронов входного слоя и равными 0,33 для остальных нейронов, формирующих обратные связи.
Зададим значения возбуждения нейронов входного слоя, соответствующие критикуемым положениям теории Дарвина, а также любовным настроениям и широте философских познаний чеховского героя.
А именно, пусть V1 = 1, V2 = V3 = 0, V4 = V5 = 0,5.
При этом оценку величины любовного позыва связываем с напряженной умственной деятельностью, а величину возбуждения нейрона 5 – с самокритичной оценкой познаний и доверия к столь заумным философским положениям.
По заданным значениям произведем первый цикл обсчета величины возбуждения остальных нейронов: V6 = … = V10 = 1 .
При втором цикле обсчета получаем V1 = V2 = V3 = 0,33 , V4 = 0,2 при неизменившихся значениях величин возбуждения других нейронов.
Третий цикл обсчета позволяет уточнить значения V6 = V7 = V8 = V9 = 0 , V10 = 1 .
Видим, что значения возбуждения нейронов, порождающих обратные связи, более не влияют на величину возбуждения нейронов входного (он же выходной) слоя.
Таким образом, сеть "высказалась" за равную действенность всех возможных утверждений о появлении человека на Земле.
Более того, если в начале исследований мы уже недостаточно уверены в предположении, что человек произошел от обезьяны, т.е. положили V1 < 1 , то это лишь усиливает правоту предположения о божественном или марсианском его происхождении.
Например, положим V1 = 0,8, V2 = V3 = 0,1 .
В результате первого же уточнения этих значений получим V1 = 0,267, V2 = V3 = 0,367 . И лишь возбуждение нейрона 10 остается неизменным, утверждающим тезис о том, что философское отношение к действительности благотворно влияет на физиологические возможности.
Конечно, мы сплутовали: мы получили то, что хотели. Совсем в духе силлогистики Аристотеля, призванной обслуживать софистику тогдашних философов. Но ведь всегда высшая идея довлеет над нашими решениями.
Построенная нейросеть с ее параметрами является лишь фрагментом, первым приближением истинной, полной, учитывающей взаимодействие всех возможных факторов сети. Построение такой сети должно опираться не только на законы диалектики, но и на теорию познания, на логические приемы индуктивного и дедуктивного мышления.
Например, мы не учли, что божественное происхождение отнюдь не гарантирует отсутствие дурного запаха и даже отсутствие хвоста. А это тотчас требует введения и положительных, и отрицательных обратных связей и т.д. Тогда, возможно, обеспечивалась бы постоянная и одинаковая сходимость величин возбуждения. Сеть давала бы один и тот же ответ, сходилась бы к нему, независимо от начальных предположений.
В то же время как с позиций диалектики согласовать правомочность всех трех предположений о происхождении человека?
Напрашивается следующая модель. Бог, конечно же, создал человека, но – на Марсе! В результате охлаждения Солнца марсианская "элита", в лице отнюдь не лучших представителей рабочего класса и трудовой интеллигенции, воспользовавшись высокими достижениями в области науки и техники (несомненно – и в области искусственного интеллекта), перебралась на Землю, где успешно спуталась с местными обезьянами.
Тогда вполне справедливо предположение о том, что в скором времени, по мере дальнейшего остывания Солнца, та формирующаяся новая "элита", что уже сейчас приобретает жилье по четыре тысячи баксов за кв. м, переберется на Венеру, где ее с нетерпением будут ждать тамошние обезьяны, вдохновленные дармовой продукцией фирм Красный Киллер и Ночная Бабочка.
Как же вводить обратные связи?
"Я дух родного твоего отца,
На некий срок скитаться осужденный
Ночной порой, а днем гореть в огне,
Пока мои земные окаянства
Не выгорят дотла".
В. Шекспир. "Гамлет, принц датский", перевод Б. Пастернака
"… все они считают меня дурным человеком. По утрам и с перепою я сам о себе такого же мнения. Но ведь нельзя же доверять мнению человека, который еще не успел похмелиться! Зато по вечерам – какие во мне бездны! – если, конечно, хорошо набраться за день, – какие бездны во мне по вечерам!"
Венедикт Ерофеев. "Москва–Петушки"
Рассмотрим непрерывную, динамически контролируемую работу уже обученной сети в реальном времени.
Пусть дядя Рамзай своими собственными глазами видел Васю, беседующего с Оксаной близ ее палатки. И было это не более пяти минут назад. Ясно, что по крайней мере еще минут на двадцать Васю следует исключить из процесса оценки достоверности последующих ситуаций. Желательно этот процесс автоматизировать. Это значит, что на входном слое должна быть учтена информация "Вася уже у Оксаны, следовательно, дальнейшее рассмотрение комбинаций с их участием нецелесообразно". И если вдруг появившийся Вовочка, прося на пряник, сообщает, что только что видел Васю у св. Аполлинарии, то дядя Рамзай, корректируя исходную информацию на текущий момент, должен игнорировать или учесть незначительно (в случае неверия собственным глазам) информацию Вовочки. Мы хотели бы, чтобы достоверность такой информации, с участием Васи и Оксаны, автоматически снижалась. Либо, наоборот, достоверность ситуаций без их участия должна увеличиваться.
И здесь мы можем не гоняться за достоверностью, требуя принадлежности ее величины диапазону [0, 1], а перейти к более общему понятию веса информации. Этот вес необходимо рассматривать как функцию времени. Ведь логично, что с течением времени вероятность участия Васи и Оксаны в последующих ситуациях должна как бы восстанавливаться.
Что необходимо для такой работы сети?
Надо с большей определенностью дифференцировать ситуации на выходном слое.
Например, если в решениях R1 и R2 замешаны не только Вася и Оксана, но и другие участники игры, то это затрудняет принятие конкретного решения только по Васе и только по Оксане. Нам необходимо корректировать дальнейшее решение по вхождению комбинации A1&C1, и не связывать, не объединять его, например, с вхождением комбинации A1&C2. Значит, надо расширить множество {Ri} принимаемых решений, повторяя ("размножая", см. лекцию 1), если необходимо, одно и то же решение для разных эталонных комбинаций.
Необходимо ввести обратную связь, осуществляющую влияние решения, осуществляемого по Васе (А1) и Оксане (С1), на достоверность или вес информации, связанные с их дальнейшим участием в складывающихся ситуациях, то есть на величины возбуждения нейронов А1 и С1, даже вопреки попыткам искусственно задать высокие значения этих величин.
Конкретными рекомендациями могут быть:
Детализация, дифференциация эталонных ситуаций, по которым принимается не только "прямое" решение Ri, но и "обратное" решение, корректирующее характер использования исходных данных.
Установление отрицательной обратной связи, которая ведет от каждого нейрона, отвечающего за решение по Васе, к нейрону А1 входного слоя.
Установление отрицательной обратной связи, которая ведет от каждого нейрона, отвечающего за решение по Оксане, к нейрону С1 входного слоя.
Установление "положительной" обратной связи от нейронов выходного слоя, отвечающих за решения по Васе, к нейрону А2, что усиливает шансы Пети в дальнейшей игре дяди Рамзая.
Установление "положительной" обратной связи от нейронов выходного слоя, отвечающих за решения по Оксане, к нейронам С2, …, С5. (Однако этого, как и указанного в пункте 4, можно и не делать.)
Строго следуя данным рекомендациям, на основе "размножения" решений, рекомендуемого в лекции 1, построим более подробную систему предикатов, которую мы воплотим с помощью нейросети:


Рис. 6.2. Нейросеть с обратными связями
Мы видим, как резко возросло число нейронов выходного слоя. Что ж, нас теперь интересуют не просто выводы, но и то, каким путем каждый из них получен. Это еще раз свидетельствует о том, что жадничать, в том числе составляя обобщенные эталоны, объединяя при этом ситуации, ведущие к одинаковому выводу, – нехорошо. Это может серьезно связывать руки при необходимости различения ситуаций. Вряд ли это жадничание правильно отражает принцип мозга, где царит избыточность, обеспечивающая обилие путей и вариантов, развиваемость, резервирование, устойчивость и надежность.
На рис. 6.2 представлен фрагмент, демонстрация начала построения возможной нейросети, которую мы вправе считать окончательным результатом наших исследований и готовы предъявить Заказчику. Чтобы сократить путаницу, мы не стали вводить положительные обратные связи.
Следует обратить внимание на то, что, вводя обратные связи, мы ограничились только лишь проблемой увеличения достоверности исходных данных на основе текущего состояния событий, предоставив читателю право рассуждения о других возможностях.
Модуль веса обратной связи в нашем случае должен быть убывающей функцией времени. Пользуясь допустимыми условностью и приблизительностью, преследуя цель скорее качественную, нежели количественную, можно рассчитать величину отрицательной обратной связи по простой формуле. Например, если считать, что на один визит Вася расходует не менее 25 минут, то вес ? одного из дендритов нейрона А1 (аналогично – других нейронов входного слоя) находится следующим образом:

Здесь:
t0
– последний момент времени вовлечения соответствующей особы в действие (хранится в составе информации о данной особе – А1, А2, С1 и др.);
t0 + 25 – ожидаемое время повторного допустимого "использования" особы в деле;
t – текущий момент поступления новых разведданных, требующих использования нейросети;
k – некоторый экспериментально подобранный демпфирующий коэффициент, возможно, зависящий от величины подаваемого возбуждения при вводе информации, чтобы разумно "погасить" влияние обратной связи, не довести ее до абсурда.
Напомним, хотя это не имеет принципиального значения, что мы используем понравившуюся нам передаточную функцию для нахождения величины Vi
возбуждения i-го нейрона:

Нейросетевое воплощение
"…Медузин сел за письменный стол и просидел с час в глубокой задумчивости; потом вдруг "обошелся посредством" руки, схватил бумагу и … написал:
Российская грамматика и логика ………………… много употребл.История и география ……………………………… употребляет довольноЧистая математика ………………………………… плохФранцузский язык …………………………………. виноградн. многоНемецкий язык …………………………………….. пива очень многоРисование и чистописание …………….………….. одну настойку
Греческий язык …………………………………….. все употребляет
После этих антропологических отметок Иван Афанасьевич записал соответственную им программу:
Ведро сантуринского ………………………………………. 16 руб.
1/2 ведра настойки ………………………………………….. 8 "
1/2 ведра пива ……………………………………………….. 4 "
2 бутылки меду ……………………………………………… 50 коп.
Судацкого 10 бутылок ……………………………………… 10 "
3 бутылки ямайского ……………………………………….. 4 "
Сладкой водки штоф ……………………………………….. 2 " 50 коп.
_____________________
Итого: 45 руб."
А.И. Герцен. "Кто виноват?"
Упражнение:
постройте нейросеть, позволяющую предсказывать действительные расходы учителя латинского языка и содержателя частной школы И.А. Медузина при оценке контингента гостей приближающегося дня тезоименитства.
Мы уже построили нейросеть для важной задачи принятия решений и вручили ее Заказчику – дяде Рамзаю. Однако, задумчиво глядя в синее небо под бодрящий рокот набегающей волны теплого течения Гольфстрим, мы не можем прогнать мыслей об обобщениях, вариациях и применениях…
Итак, еще раз тщательно проследим принцип динамического совмещения процесса обучения системы управления с процессом выдачи решений, изложенный выше, и установим в схеме на рис. 7.2
целесообразность, место и способ использования нейронной сети как основного реального средства искусственного интеллекта. Прежде всего, мы понимаем, что основным естественным и целесообразным местом применения нейросети здесь является база знаний, ранее реализованная с помощью ассоциативной памяти (рис. 7.1).
Нам только надо позаботиться о том, чтобы "крутились" там не численные значения информации, а вес этой информации или ее достоверность. То есть не сама информация должна обрабатываться нейросетью, а ее логический эквивалент. Ведь мы поняли, что принцип искусственного интеллекта направлен на параллельную обработку логических высказываний, а вовсе не ориентирован напрямую на числовую обработку информации, как это делается при решении некоторых "нейроподобных" задач при использовании нейросети в роли спецпроцессора.
Пусть нейросеть в роли базы знаний имеет текущий вид, представленный на рис. 7.3.
Нейроны-рецепторы оказались закрепленными за значениями элементов входного вектора. Это значит, что в режиме обучения (или в процессе динамической корректировки) установилось соответствие на основе положения "величина возбуждения данного p-го нейрона входного слоя принимает значение достоверности того, что xi= xi(p)
.
Здесь могут фигурировать не точные значения параметров, а некоторые диапазоны их изменения, как это указывалось в 3.2.
Как мы ранее делали, при обучении мы полагаем эту достоверность равной единице, а в процессе распознавания может быть что угодно, даже не удовлетворяющее свойству полноты событий.

Рис. 7.3. Управляющая система с нейросетью
"Показывая" сети на этапе обучения различные эталоны, методом трассировки мы можем добиться установления соответствия вида {Входы xi}

Для нахождения этих значений управляющих воздействий в зависимости от значений исходных данных может быть использовано моделирование, наряду с экспериментом или с экспертными оценками.
Таким образом, модель, эксперимент или эксперт играют роль учителя. (Мы ранее уже высказали сомнение насчет существования и действенности "чистого" самообучения.)
Первоначально обученная таким образом нейросеть может быть уже использована в рабочем режиме (распознавания) и в режиме совместной работы с моделью. При этом мы понимаем, что нейросеть обучена недостаточно, и, подобно пристрелке реперов "в свободное от работы" время, мы пытаемся с помощью модели испытать и, в случае необходимости, дополнить знания нейросети.
Модель случайно или направленно – по обоснованному плану "выбрасывает" некоторую ситуацию, характеризующуюся значением компонент входного вектора Х. По каждой компоненте определяется вес или достоверность того, что ее значение совпадает с подмножеством значений этой компоненты, представленных входным слоем нейросети, или с диапазонами значений этой компоненты.
Например, сеть "знает" реакцию на значение (опустим индекс) x = 2, x = 5, x = 6. Модель выбросила значение х = 5,7. Это может означать необходимость формирования значений возбуждения Vx=2 = 0 , Vx=5 = 0,3 , Vx=6 = 0,7 . Здесь индексы возбуждений указывают нейроны входного слоя, закрепленные за данным значением параметра. Так делается по всем компонентам входного слоя.
Пусть, "пройдя" по сети, данные возбуждения входного слоя привели к преодолению порога возбуждения нейронов выходного слоя R5 ( VR5 = a ), R7 ( VR7 = b ), R12 ( VR12 = c ). При этом нейрону R5 соответствует вектор управляющих воздействий Y5 = (y1(5), y2(5), …, yn(5)) , нейрону R7 – вектор Y7 = (y1(7), …, yn(7)) , нейрону R12 – вектор Y12 = (y1(12), …, yn(12)) . Тогда мы находим предполагаемый ответ нейросети:

Подставляем данное решение в модель и устанавливаем, удовлетворяет ли нас оно, – например, по величине промаха. Если удовлетворяет, мы делаем положительный вывод об обученности нейросети и продолжаем ее испытание по другим исходным данным. Если нет – сеть необходимо "доучить", продемонстрировав самый высокий логический уровень обратной связи.
Для этого мы должны ввести в действие новые рецепторы, закрепив их за теми значениями исходных данных или их диапазонами, которые ранее не были представлены. Например, нам придется закрепить рецептор за значением х = 5,7.
Далее, мы должны выделить нейрон выходного слоя и закрепить его за соответствующим правильным решением, которое мы должны получить с помощью модели.
Далее, мы должны выполнить трассировку для того, чтобы задание нового эталона с единичной достоверностью исходных данных приводило к максимальному возбуждению выделенного нейрона выходного слоя, ответственного за получение правильного решения.
Таким образом, сеть может обучаться до тех пор, пока не перестанет давать "сбоев". А поскольку в вероятностном аспекте это вряд ли возможно, то в таком режиме она должна работать в течение всего жизненного цикла, реализуя известную пословицу "Век живи – век учись"…
Здесь наглядно представлена замечательная возможность нейросети: табличная аппроксимация функции многих переменных , снабженная процедурой интерполяции (экстраполяции) для нахождения произвольного значения вектора-аргумента и приближенного соответствующего значения векторной функции. При этом входной вектор возбуждений рецепторов преобразуется в максимальное или усредненное значение возбуждения нейронов выходного слоя, указывающего на соответствующее значение вектора-функции. Так что практически столь простым способом мы построили аппроксимацию векторной функции от векторного аргумента!
Такую аппроксимацию можно выполнить и "в более явном виде", ибо каждая компонента yj решения Y = {y1,…, yп} может отыскиваться отдельно в результате предварительной трассировки (рис. 7.4). То есть сеть может быть построена и обучена так, чтобы заданное значение Х = {x1,…, xт} приводило к максимальному (или усредненному) значению возбуждения нейрона выходного слоя, указывающего соответствующее значение y1
, к максимальному (или усредненному) значению возбуждения другого нейрона выходного слоя, указывающего на значение у2
и т.д. Выходной слой оказывается разбит на области, каждая из которых закреплена за своим параметром уi
, i =1,…, п. Тогда полученное преобразование можно условно записать X

Следует обратить внимание не только на высокую производительность такого рода самообучающихся систем в рабочем режиме, но и на их адаптивность, развиваемость, живучесть и т.д.

Рис. 7.4. Раздельное нахождение управляющих параметров с помощью нейросети
Самообучение на основе ситуационного управления
Известной основой аппаратной поддержки самообучающейся системы управления является ассоциативная вычислительная система .
Главное отличие ассоциативной ВС от обычной системы последовательной обработки информации состоит в использовании ассоциативной памяти или подобного устройства, а не памяти с адресуемыми ячейками.
Ассоциативная память (АП) допускает обращение за данными на основе их признака или ключевого слова: имени, набора характеристик, задания диапазона и т.д.
Распространенный вид АП – таблица с двумя столбцами: "запросное поле – ответное поле". Строка таблицы занимает регистр памяти. По ключевому слову обрабатываются запросные поля: производится поиск на основе сравнений и выдается результат из одного (или более) ответных полей. При помощи маскирования можно выделить только те поля в ключевом слове, которые нужно использовать при поиске для сравнения.
Типичными операциями сравнения, выполняемыми ассоциативной памятью, являются: "равно – не равно", "ближайшее меньше чем – ближайшее больше чем", "не больше чем – не меньше чем", "максимальная величина – минимальная величина", "между границами – вне границ", "следующая величина больше – следующая величина меньше" и др. Т.е. все это – операции отношения и определения принадлежности.
Поскольку ассоциативные ВС характеризуются только активным использованием АП в вычислениях, то в целом эти ВС обладают обычными свойствами, могут производить сложные преобразования данных и принадлежать типу ОКМД (STARAN, PEPE) или МКМД. Для параллельного обращения (для ускорения поиска) АП разбита на модули (32 модуля – в STARAN).
Когда в 1980 г. был провозглашен т.н. "Японский вызов" о построении ВС сверхвысокой производительности, то одним из пунктов была указана необходимость самого широкого использования принципов самообучающихся систем – систем, способных накапливать опыт и выдавать результат решения задачи без счета самой задачи, – на основе ассоциации и интерполяции (экстраполяции).
Это значит, что применение ассоциативных ВС неотделимо от проблемы искусственного интеллекта.
Покажем, что ничего существенно нового в практику человеческого мышления ассоциативные машины не вносят, что это привычный способ использования интерполяционных таблиц, например таблицы логарифмов.
Предположим, мы пользуемся значениями функции y = f(x). Мы можем запрограммировать счет этой функции на персональном компьютере, и каждый раз, когда нам надо, задаем x и запускаем программу, пользуясь прекрасным современным сервисом.
Предположим, та же функция сложна, а ее счет – важный элемент алгоритма управления в реальном времени. Решение приходит сразу: зададим эту функцию таблично, а для ускорения выборки включим в ВС ассоциативную память. Предусмотрим на ней операции, позволяющие производить простейшую интерполяцию. А именно, для данного значения x найти наибольший x1



надо только быть уверенным в достижении нужной точности.
Однако в повседневной жизни мы очень часто решаем трудно формализуемые задачи, подобно предложенной дядей Рамзаем, когда составить алгоритм решения совсем не просто. Но мы учимся, обретаем опыт, затем оцениваем складывающуюся ситуацию на "похожесть" и принимаем решение.
Простейшая задача: как мы автоматически определяем, на сколько надо повернуть рулевое колесо, чтобы остаться на дороге? Ведь первый раз мы въезжали в бордюр! Значит, некая таблица постепенно сложилась и зафиксировалась в нашем сознании.
Пожалуй, наиболее полно автоматически и с наибольшей практичностью решение задачи самообучения представлено в артиллерии, точнее – в правилах стрельбы.
После занятия огневой позиции подготовка установок для ведения огня занимает много времени. На рассчитанных установках по каждой цели производится пристрелка, когда цель захватывается в широкую вилку, затем по наблюдениям вилка "половинится" до тех пор, пока на середине узкой вилки не переходят на поражение.
После стрельбы следует замечательная команда "Стой, записать...", по которой наводчик на щите орудия пишет номер цели и все пристрелянные установки по ней. Такая работа проделывается и по фиктивным целям – реперам. Постепенно при "работе" на данной местности запоминаются пристрелянные установки по многим целям и реперам. С их появлением и развитием подготовка данных по вновь появляющимся целям резко упрощается, т.к. сводится к переносу огня от ближайшей цели или репера, т.е. к внесению поправок по дальности и направлению. Доказано, что при этом достаточно сразу назначать захват цели в узкую вилку, т.е. пристрелка упрощается. Правила стрельбы существуют века, однако вряд ли кто-то осознавал теоретически, что речь идет о реализации самообучающейся системы, у которой не существует аналога!
Для трудно формализуемых задач управления или для увеличения производительности вычислительных средств известно т.н. ситуационное управление, предложенное Д.А. Поспеловым [23]. Оно заключается в том, что для каждого значения вектора, описывающего сложившуюся ситуацию, известно значение вектора, описывающего то решение, которое следует принять. Если все ситуации отразить невозможно, должно быть задано правило интерполяции (аналог интерполяции, обобщенной интерполяции).
Пусть исходная ситуация характеризуется вектором X = {x1, …, xm} . По значению X, т.е. по его компонентам, принимается решение Y, также представляющее собой вектор Y = {y1, ..., yn} .
(Значения X и Y могут определяться целыми и вещественными, булевыми. Изначально они могут иметь нечисловую природу: "темнее – светлее", "правее – левее", "ласковее – суровее" и т.д. Мы не будем рассматривать проблему численной оценки качественных или эмоциональных категорий.)
Предположим, для любых двух значений X1
и X2
, а также Y1
и Y2
определено отношение xi(1)

(или наоборот), yj(1)

(или наоборот).
Структура ассоциативной памяти и общий вид ее обработки показаны на рис. 7.1.
Пусть поступила входная ситуация Х, для которой необходимо найти решение Y. В АП находятся два вектора X1
и Х2
, минимально отличающиеся по всем координатам от вектора Х. Для этих векторов там же записаны векторы решения Y1
и Y2
соответственно. Однако если для компоненты xi
выполняется условие xi

(xi?xi(1)) , то желательно выполнение условия xi

( xi

), i = 1, ..., m. Эта желательность обусловлена преимуществом интерполяции по сравнению с экстраполяцией. Таким образом, находится "вилка", которой принадлежит входная ситуация.

Рис. 7.1. Управление с помощью ассоциативной памяти
Тогда, опираясь на известные решения на границах этой вилки, необходимо выдать промежуточное решение для данной ситуации. Это можно сделать методом той же обобщенной интерполяции:

, а также Х1
и Х2
.
Если известно, что точность Y достаточна, принципиально возможно дополнение АП новой строкой

т.е. информацией о новом полученном опыте.
Однако целесообразная динамика развития и уточнения АП как базы знаний представляется иной. Далеко не всегда будет правильным развитие базы знаний только на основе ошибочного принятия решений. "Учение на ошибках" может привести к трагедии (или к частному срыву процесса управления), особенно на этапе обучения системы.
Обучение системы целесообразно проводить на достаточно точной модели, максимально использующей точный расчет компонент решения. Применение модели для обучения используется не только на специально предусмотренном этапе обучения системы, но и вне реального цикла управления, т.е. когда система работает в режиме дежурства, параллельно с функциональным контролем. Такой алгоритм ее работы представлен на рис. 7.2.

Рис. 7.2. Схема самообучения с ассоциативной памятью и моделью
Это значит, что применение ассоциативных ВС неотделимо от проблемы искусственного интеллекта.
Покажем, что ничего существенно нового в практику человеческого мышления ассоциативные машины не вносят, что это привычный способ использования интерполяционных таблиц, например таблицы логарифмов.
Предположим, мы пользуемся значениями функции y = f(x). Мы можем запрограммировать счет этой функции на персональном компьютере, и каждый раз, когда нам надо, задаем x и запускаем программу, пользуясь прекрасным современным сервисом.
Предположим, та же функция сложна, а ее счет – важный элемент алгоритма управления в реальном времени. Решение приходит сразу: зададим эту функцию таблично, а для ускорения выборки включим в ВС ассоциативную память. Предусмотрим на ней операции, позволяющие производить простейшую интерполяцию. А именно, для данного значения x найти наибольший x1



надо только быть уверенным в достижении нужной точности.
Однако в повседневной жизни мы очень часто решаем трудно формализуемые задачи, подобно предложенной дядей Рамзаем, когда составить алгоритм решения совсем не просто. Но мы учимся, обретаем опыт, затем оцениваем складывающуюся ситуацию на "похожесть" и принимаем решение.
Простейшая задача: как мы автоматически определяем, на сколько надо повернуть рулевое колесо, чтобы остаться на дороге? Ведь первый раз мы въезжали в бордюр! Значит, некая таблица постепенно сложилась и зафиксировалась в нашем сознании.
Пожалуй, наиболее полно автоматически и с наибольшей практичностью решение задачи самообучения представлено в артиллерии, точнее – в правилах стрельбы.
После занятия огневой позиции подготовка установок для ведения огня занимает много времени. На рассчитанных установках по каждой цели производится пристрелка, когда цель захватывается в широкую вилку, затем по наблюдениям вилка "половинится" до тех пор, пока на середине узкой вилки не переходят на поражение.
После стрельбы следует замечательная команда "Стой, записать...", по которой наводчик на щите орудия пишет номер цели и все пристрелянные установки по ней. Такая работа проделывается и по фиктивным целям – реперам. Постепенно при "работе" на данной местности запоминаются пристрелянные установки по многим целям и реперам. С их появлением и развитием подготовка данных по вновь появляющимся целям резко упрощается, т.к. сводится к переносу огня от ближайшей цели или репера, т.е. к внесению поправок по дальности и направлению. Доказано, что при этом достаточно сразу назначать захват цели в узкую вилку, т.е. пристрелка упрощается. Правила стрельбы существуют века, однако вряд ли кто-то осознавал теоретически, что речь идет о реализации самообучающейся системы, у которой не существует аналога!
Для трудно формализуемых задач управления или для увеличения производительности вычислительных средств известно т.н. ситуационное управление, предложенное Д.А. Поспеловым [23]. Оно заключается в том, что для каждого значения вектора, описывающего сложившуюся ситуацию, известно значение вектора, описывающего то решение, которое следует принять. Если все ситуации отразить невозможно, должно быть задано правило интерполяции (аналог интерполяции, обобщенной интерполяции).
Пусть исходная ситуация характеризуется вектором X = {x1, …, xm} . По значению X, т.е. по его компонентам, принимается решение Y, также представляющее собой вектор Y = {y1, ..., yn} .
(Значения X и Y могут определяться целыми и вещественными, булевыми. Изначально они могут иметь нечисловую природу: "темнее – светлее", "правее – левее", "ласковее – суровее" и т.д. Мы не будем рассматривать проблему численной оценки качественных или эмоциональных категорий.)
Предположим, для любых двух значений X1
и X2
, а также Y1
и Y2
определено отношение xi(1)

(или наоборот), yj(1)

(или наоборот).
Структура ассоциативной памяти и общий вид ее обработки показаны на рис. 7.1.
Пусть поступила входная ситуация Х, для которой необходимо найти решение Y. В АП находятся два вектора X1
и Х2
, минимально отличающиеся по всем координатам от вектора Х. Для этих векторов там же записаны векторы решения Y1
и Y2
соответственно. Однако если для компоненты xi
выполняется условие xi

(xi?xi(1)) , то желательно выполнение условия xi

( xi

), i = 1, ..., m. Эта желательность обусловлена преимуществом интерполяции по сравнению с экстраполяцией. Таким образом, находится "вилка", которой принадлежит входная ситуация.

Рис. 7.1. Управление с помощью ассоциативной памяти
Тогда, опираясь на известные решения на границах этой вилки, необходимо выдать промежуточное решение для данной ситуации. Это можно сделать методом той же обобщенной интерполяции:

, а также Х1
и Х2
.
Если известно, что точность Y достаточна, принципиально возможно дополнение АП новой строкой

т.е. информацией о новом полученном опыте.
Однако целесообразная динамика развития и уточнения АП как базы знаний представляется иной. Далеко не всегда будет правильным развитие базы знаний только на основе ошибочного принятия решений. "Учение на ошибках" может привести к трагедии (или к частному срыву процесса управления), особенно на этапе обучения системы.
Обучение системы целесообразно проводить на достаточно точной модели, максимально использующей точный расчет компонент решения. Применение модели для обучения используется не только на специально предусмотренном этапе обучения системы, но и вне реального цикла управления, т.е. когда система работает в режиме дежурства, параллельно с функциональным контролем. Такой алгоритм ее работы представлен на рис. 7.2.

Рис. 7.2. Схема самообучения с ассоциативной памятью и моделью
Нейросеть для решения задачи логического вывода
Рассмотрим предварительно один аспект обучения нейросети методом трассировки.
Первоначально (лекция 4), поясняя "схемотехнический" подход к построению нейросети, мы предполагали, что никаких связей ("проводочков") не было, а мы их проложили, исходя из реализуемых
логических функций. Обобщив подход на нечеткую логику (предполагающую вхождение элементов в состав множества
с некоторой вероятностью), а также логику передаточных функций, мы заявили, что нашли способ построения уже обученных нейросетей.
Впоследствии (лекции 5 и 6) мы заявили, что нас не смущает отсутствие некоторых связей в "готовых" сетях. Мы их введем как "проводочки", если сочтем это целесообразным.
Таким образом, несовершенство нейросети не стало для нас преградой. А если предположить, как при
"схемотехническом" подходе, что первоначально в сети вообще никаких связей нет, ее матрица
следования пуста, а нам предстоит создать эту сеть полностью? Логично, что в ней будут присутствовать
только те связи, которые обеспечивают ее обучение. То есть мы сразу можем строить обученную нейросеть
— нейросеть, синапсические связи в которой имеют единичный (максимальный) вес.
Составим (рис. 8.1) нейросеть, соответствующую фрагменту беспредельной
базы знаний о жителях далекого таежного села.
Нейросеть будет отражать два уровня моделирования дедуктивного мышления, и состоять из двух частей.
Фактографическая нейросеть отражает факты, содержащиеся в БЗ. Понятийная нейросеть отражает правила вывода, оперируя понятиями – процедурами БЗ.
Моделируя лишь дедуктивное мышление, ограничимся возможностью дополнения фактографической нейросети, добываемой информацией на основе выводов, производимых с помощью понятийной нейросети . Развитие же понятийной нейросети , т.е. дополнение БЗ новыми правилами, требует решения проблемы индуктивного мышления, т.е. мышления более высокого уровня, пока не столь широко доступного.
Сформируем начальный вид фактографической нейросети (рис. 8.1).
Это – начальный вид, т.к. мы надеемся дополнить ее до состояния насыщения в результате фиксирования
новых фактов, получаемых в длительном рабочем режиме эксплуатации, в процессе решения задач логического вывода. Такое развитие фактографической нейросети позволит исключить трудоемкий повторный вывод, воспользоваться однажды установленным фактом, словно записью на щите орудия о пораженных целях.
Для реализации правил построим понятийную нейросеть , фрагмент которой показан на
рис. 8.2 .
Рецепторный слой, несомненно, содержит элементы избыточности. Однако различие в обозначениях повторяющихся
переменных (и закрепленных за ними рецепторов) позволяет избежать коллизии при формировании выводов на основе формального описания правил.
Пусть задана та же сложная цель
дядя (X, Y).
Для нее необходимо сформировать все пары переменных X и Y, для которых справедливо утверждение "Х
является дядей Y".

Рис. 8.1. Начальный вид фактографической нейросети
Выберем следующую передаточную функцию:
Порог h подбирается экспериментально, в данном случае, кажется, целесообразно положить h = 0,4 .

Рис. 8.2. Понятийная нейросеть
Чтобы максимально возбудить нейрон выходного слоя, ответственный за дядю, необходимо подать высокий
сигнал возбуждения на рецепторы, передающие возбуждение этому нейрону, выполнив все варианты непротиворечивого
связывания переменных X, Q, P, Y.
Таким образом, надо реализовать ту же схему перебора с возвратом, что была рассмотрена ранее, — схему backtracking'а.
Проследим по шагам необходимые действия:
Полагаем Х = иван."
В процедуре Родитель находим Q = мария."
В той же процедуре находим Р = василий."
Однако, в той же процедуре не находим указаний на то, что Василий является чьим-то родителем."
Возвращаемся на шаг назад, пытаясь изменить связывание переменной Р, но не находим нового варианта связывания."
Возвращаемся еще на шаг и т.д. – повторяем весь ход рассуждений, рассмотренных в
подразделе 8.1 ."
После нахождения пары (василий, елена) следует развить фактографическую сеть, дополнив ее выходной слой нейроном в соответствии с понятием дядя и установив связи с ним от василия и елены.
Это может быть сделано двумя способами.
Первый способ повторяет весь ход логических рассуждений, связывая высказывания, приведшие к данному
заключению. Тогда в результате решения всевозможных задач вывода установится окончательный вид фактографической нейросети , представленный на рис. 8.3. (Для упрощения рисунка некоторые входные связи недозволенно объединяются в "кабель".)
Как работать с этой сетью?

увеличить изображение
Рис. 8.3. База Знаний Антрополога–Исследователя
Можно себе представить два режима этой работы: для фискального органа — налоговой инспекции, требующей
общей картины социального состояния, и для информационно-аналитической службы безопасности, интересующейся
гражданами индивидуально, по выбору и привлечению.
А именно, если мы "засветим" (сообщив единичное возбуждение) все нейроны-рецепторы, то
мы сможем прочесть все, что нейросеть "знает" о всех своих клиентах: кто из них мужчина, кто
— женщина, в каком родстве они состоят.
Но мы можем спросить сеть лишь о некоторых персонажах. Например, мы можем возбудить на входе нейроны-рецепторы,
соответствующие Ивану и Василию. Мы получим информацию о том, что они, несомненно, мужчины.
Но подозрительно высокого возбуждения достигнут нейроны, отвечающие за факт, что Марья — мать Ивана и она же — мать Василия.
Подозрительно возбудятся и нейроны, отвечающие за факты Иван — брат Василия и Василий — брат Ивана, Юрий — дядя Ивана и др. Тогда мы решаем: "А ну-ка, возбудим нейрон-рецептор, соответствующий Марье, и посмотрим, что интересного нам сеть сообщит!" И сеть возбуждением своих нейронов нам сообщает: "Да, действительно, Марья — мать Ивана и Василия".
Заметим, что мы можем подавать на входе и неединичные значения возбуждений. Например, установив,
что в "деле" участвовал не то Иван, не то Василий (уж очень они похожи!), мы можем по принципу
"фифти-фифти" задать соответствующие значения возбуждений равными 0,5 и установить высокую величину возбуждения нейрона, соответствующего дяде и того и другого — Юрию. И тогда логично возложить на него ответственность за нерадивое воспитание племянников.
Таким образом, составляя эту нейросеть, мы руководствовались желанием сохранить причинно-следственные
логические связи, обусловленные правилами. Это отражает ориентацию нейросети на пытливый ум, методом индуктивного мышления старающийся выяснить, какие факты достаточны для установления, например, того, что Юрий — дядя Ивана. Мы даже назвали эту нейросеть Базой Знаний Антрополога-Исследователя. Здесь же мы пошли на организацию коры. Мы справедливо решили, что все выводы данной сети должны быть равноправными и служить как формированию выводов "внутри себя", так и применению "вне" — для решения некоторой глобальной задачи, сверхзадачи. Равноправность и внешнее использование, в том числе для логической надстройки сети, для получения новых знаний по новым вводимым фактам и правилам, требует ревизии и особого установления величин возбуждения нейронов, что мы и отразили в передаточной функции.
Но мы ловим себя на лукавом мудрствовании… "Зачем так сложно?" — спросит рядовой гражданин, к каковому следует отнести жителя далекого села. — "Какое мне дело до намеков твоих? Ты давай напрямик,
факты давай!.."
Действительно, зачем нам знать и делать вывод о том, что Юрий — дядя Ивана, потому что он — брат Марьи? Мы можем эти два факта задать независимо, предварительно рассчитав по понятийной нейросети.
Тогда фрагмент БЗ, которую мы назвали Базой Знаний Участкового Уполномоченного, представлен на рис. 8.4, и мы можем вздохнуть облегченно!
И не надо никакой коры! Строго, по-военному и как в анкете: посылка — следствие! Не надо сомнений,
размышлений, ревизий и прочего вольнодумствия!
Таким образом, реализовав все причинно- следственные связи, мы построили нейросеть, отображающую только
факты. Размножив ее для работы многих пользователей, можно получить достаточную информацию и исключить из рассмотрения правила вывода.

увеличить изображение
Рис. 8.4. База Знаний Участкового Уполномоченного
Рассмотренная схема работы с нейросетью отображает модель дедуктивного мышления. Но можно ли на основе
полученной нейросети произвести обратные действия, построить обобщения, получить правила, достойные индуктивного мышления?
По-видимому, необходим анализ нейросети, сохранившей причинно-следственные связи, для выделения идентичных
подструктур, объединяющих факты из общих процедур – носителей понятий.
Например, пути (статические цепочки), приводящие к выводу дядя (василий, елена), дядя (юрий, иван) , дядя (юрий, василий) в одинаковом порядке связывают "представителей" одних и тех же процедур. Тогда, выбрав вместо конкретных переменных их абстрактное обозначение, можно восстановить правило вывода. А это уже гипотеза — важный элемент индуктивного мышления. На основе этой гипотезы может быть развита понятийная нейросеть . Но гипотеза будет оставаться гипотезой, пока в достаточной мере не подтвердится практикой.
Тогда нейросеть обретает возможность широкого развития. Ведь если население села пополнилось родившимся
младенцем, то правильность построенного правила (гипотезы) может быть успешно проверена!
…Да, мы вправе выбирать способ мышления как принцип жизни — для ее облегчения…
ПРОЛОГ-программа
Следуя различными путями дедуктивного и индуктивного мышления, осуществляя различные парадигмы обучения,
человек стремился автоматизировать логику мышления, немыслимую без формализации. Продуктом этой деятельности
явились такие языки логического вывода, как ЛИСП и ПРОЛОГ. Язык ПРОЛОГ следует считать венцом усилий по автоматизации логического вывода, эффективно описывающего, в частности, экспертные системы.
ПРОЛОГ представляет базу знаний как совокупность фактов и правил (вывода). Процедурная структура позволяет включать конструкции любых других алгоритмических языков. То есть он является логической надстройкой,
сублимирующей лишь операции логического вывода. Формулируется цель логического вывода, и если она не противоречива, выявляются факты, из которых эта цель следует.
И сознавая, что Природа создала единственное средство мышления — мозг, мы снова и снова пристально
раздумываем, как же реализовать то, что гениально воплощено в языке логического программирования ПРОЛОГ?
…Представьте себе село, затерянное в далекой таежной глуши. Навечно изолированные от Большой Жизни, его обитатели долгими зимними вечерами, в перерывах благотворного интеллектуального напряжения игры "Тигра идет", в сумраке демократических потугов вооружившись мозолистыми кулаками, выясняют степень взаимного родства.
И тут являетесь вы! Словно светоч озарения, сосланный за непримиримость свободолюбивых устремлений,
вы, наконец, находите для себя непаханое поле действительно яркой деятельности, полной гуманизма и самопожертвования.
Вы решаетесь положить конец сомнениям, и подобно искусному укротителю, внедряете важные элементы государственного акта переписи населения…
Рассмотрим упрощенную задачу в виде ПРОЛОГ-программы, содержащую все характерные элементы решения проблемы удовлетворения (сложной) цели на основе лишь фрагмента базы знаний (БЗ), содержащего факты и правила.
Факты — клозы (отдельные предикаты-высказывания принято называть клозами), которые не содержат правых частей, правила — клозы, которые содержат правые части; одноименные факты и правила объединяются в процедуры.
База знаний
Процедура "мужчина":
мужчина (иван)
мужчина (василий)
мужчина (петр)
мужчина (федор)
мужчина (юрий)
Процедура "женщина":
женщина (марья)
женщина (ирина)
женщина (ольга)
женщина (елена)
Процедура "родитель":
родитель (марья, иван) (Читать: "Марья — родитель Ивана")
родитель (иван, елена)
родитель (марья, василий)
родитель (федор, марья)
родитель (петр, ирина)
родитель (петр, иван)
родитель (федор, юрий)
Процедура "мать":
мать (X, Y): — женщина (X), родитель (X, Y)
Процедура "отец":
отец (X, Y): — мужчина (X), родитель (X, Y)
Процедура "брат":
брат (X, Y): — мужчина (X), родитель (P,X), родитель (P, Y), X<>Y
Процедура "сестра":
сестра (X, Y): — женщина (X), родитель (P, X), родитель (P, Y), X<>Y
Процедура "дядя":
дядя (X,Y): — брат (X, P), родитель (P, Y)
Пусть задана некоторая сложная (т.е. опирающаяся не на факт, а требующая вывода) цель, с которой мы обратились в эту БЗ, например:
дядя (X, Y) (запись цели образует фрейм),
и ее решение (вывод) заключается в нахождении всех пар переменных (имен объектов) X и Y, для которых справедливо утверждение "X является дядей Y".
Для решения такой задачи используется прием трансформации цели, который заключается в рекурсивном
переборе различных вариантов подстановки вместо предикатов, составляющих сложную цель, фактов или правых частей клозов соответствующих процедур. Производится фиксация варианта связывания переменных и унификация, при которой отбрасываются несовместимые варианты связывания, противоречащие фактам. Варианты связывания всех переменных, прошедшие все этапы унификации, являются решением.
То есть для решения данной задачи необходимо действовать следующим образом.
Находим первый (а он и единственный) предикат цели дядя (X, Y) . Находим в БЗ процедуру с этим именем и заменяем найденный предикат правой частью этой процедуры. Получим трансформированную цель — фрейм
брат (X, P), родитель (P, Y).
К первому предикату этого фрейма применяем аналогичные действия, получаем фрейм
мужчина (X), родитель (Q, X), родитель (Q, P), X<>P, родитель (P,Y)
(во избежание коллизии, развивая фрейм цели, вводим новые переменные, отличные от тех, которые до того уже были использованы.)
Вновь входим в процедуру с именем первого предиката цели. Начинаем первый уровень ветвления. А именно, первый клоз процедуры — факт мужчина (иван). С его помощью производим первое связывание переменных, т.е. подстановку конкретного значения. Предикат цели, породивший факт, т.е. это связывание, может быть исключен из трансформируемой цели, т.е. заменен своей "пустой" правой частью:
родитель (Q, иван), родитель (Q, P), иван <>P, родитель (P,Y).
Обращаемся к процедуре "родитель", начиная второй уровень ветвления. Первый клоз этой процедуры
родитель (марья, иван) определяет дальнейшее связывание переменных:
родитель (марья, Р), иван <> P, родитель (P, Y).
Вновь входим в процедуру "родитель" (третий уровень ветвления), находим клоз родитель (марья, иван) . Трансформируем цель — получаем новый фрейм:
иван <> иван, родитель (иван, Y).
Получаем противоречие, т.е. не проходит унификация.
Ищем на данном шаге ветвления другой вариант связывания, находим следующий клоз:
родитель (марья, василий).
Трансформируем цель:
иван <> василий, родитель (василий, Y)

Вновь входим в процедуру "родитель", но не находим там клоза, в котором василий указан как чей-либо родитель. Т.е. вновь не проходит унификация — установление совместимости варианта связывания переменных.
Возвращаемся на шаг ветвления назад. (Реализуем стратегию поиска с ветвлением и возвращением назад
— "backtraking".) На втором уровне ветвления пробуем клоз, в котором иван указан как сын: родитель (петр, иван) . Цель трансформируется в следующий фрейм:
родитель (петр, Р), иван <> P, родитель (P, Y).
Вновь ( на третьем уровне ветвления) обращаемся к процедуре "родитель" и выбираем первый клоз, в котором петр указан как отец — родитель (петр, ирина).
Цель трансформируется:
иван <> ирина, родитель (ирина, Y)

Входим в процедуру "родитель", но не находим там клоза, в котором ирина указана как родитель (не проходит унификация).
Возвращаемся на второй уровень ветвления и не находим там больше клозов, где иван указан как сын. Возвращаемся на первый уровень ветвления и в процедуре "мужчина" выбираем для последующего испытания следующий клоз мужчина (василий).
Цель принимает вид фрейма
родитель (Q, василий), родитель (Q, P), василий <> Р, родитель (P, Y).
Теперь на втором уровне ветвления находим первый (и единственный) клоз, в котором василий указан как сын. Цель трансформируется в соответствии с новым связыванием переменных, обусловленным найденным клозом родитель (марья, василий):
родитель (марья, Р), василий <> P, родитель (P, Y).
На третьем уровне ветвления находим первый клоз, где марья — родитель: родитель (марья, иван). Связываем тем самым переменные, цель трансформируется
василий <> иван, родитель (иван, Y)

Находим в процедуре "родитель" первый клоз, в котором иван указан как родитель — родитель
(иван, елена) . Цель выродилась, значит
дядя (X, Y) = дядя (василий, елена) — одно из решений задачи.
Продолжив перебор так, словно на данном шаге унификация не прошла, можно найти остальные решения: дядя (юрий, иван), дядя (юрий, василий).
В основе распараллеливания решения этой задачи лежит способ размножения вариантов на основе трансформации
цели. Способ обеспечивает отсутствие "backtracking'а" (ветвление есть, а возврата назад нет), простоту самой процедуры вывода, возможность неограниченного использования ИЛИ-параллелизма (одновременной независимой обработки многих вариантов связывания переменных), конвейерную реализацию И-параллелизма (распараллеливания обработки одного варианта связывания переменных на конвейере, т.к.каждый раз обрабатывается лишь первый предикат каждого фрейма).
Однако представляется, что нейросетевая технология, основанная на естественном параллелизме, может
оказаться эффективной.
Анализ примера
Проверим, достаточны ли наши действия по построению нейросети. Показывает ли она на правильные решения по тем эталонным ситуациям, по которым создавалась логическая схема? Однозначен ли ее ответ при предъявлении различных эталонных ситуаций? Одинаковы ли величины возбуждения нейронов выходного слоя при предъявлении различных эталонов, что служит помехоустойчивости нейросети и возможности ее вложения в другие нейросети при формировании "длинных" логических цепочек рассуждений? Необходима ли коррекция параметров сети (порогов и весов связей) для ее правильной работы?
Отметим, что опыт исследований склоняет в пользу преимущественного применения передаточной функции 3. Она обладает таким важным свойством (если позволяет порог), как ассоциативность, позволяющая "собирать" сигнал независимо от пути прохождения возбуждения.
Выберем эту передаточную функцию, предположив, что веса всех связей равны единице, общий для всех нейронов порог h = 0,3.
Рассчитаем для различных эталонных ситуаций значения возбуждения нейронов выходного слоя и, следовательно, определим принимаемые решения. Расчеты сведены в табл. 9.1.
| 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 3 |
| 1 | 1 | 1 | 1 | 1 | 3 | 3 | 2 | 1 |
| 1 | 1 | 1 | 0 | 3 | 1 | 0 | 0 | 0 |
| 4 | 0 | 5 | 3 | 0 | 2 | 0 | 1 | 1 |
| 4 | 1 | 2 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 2 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 2 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 3 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Анализируя таблицу, видим, что даже при предъявлении эталонов сеть работает неправильно.
По некоторым эталонам (столбцы 1, 2 и 8) она дает неоднозначный ответ.
Тем самым сеть демонстрирует "побочный эффект". Из-за наличия общих событий, составляющих разные ситуации, эти события определяют одинаковый исход даже в том случае, если другие события обеспечивают различие ситуаций. Так, конъюнкция Х1

Далее, анализ таблицы показывает, что даже при правильном ответе величины возбуждения нейронов выходного слоя, закрепленные за разными решениями, различны. Более того, эти величины могут различаться даже при предъявлении эталонов, требующих одного и того же решения (столбцы 1 и 2, 3 и 4, 8 и 9).
Таким образом, требуется корректировка параметров нейросети.
Практический подход и обоснование структуры логической нейронной сети для системы принятия решений
В лекции 1 проводилось обоснование системы принятия решений (СПР) на основе основных положений математической логики событий. В последующих лекциях рассматривались примеры практического построения СПР. Однако в предыдущем разделе данной лекции возникли проблемы, связанные с тем, что при заданной структуре и количестве нейронов в обучаемой нейронной сети не всегда удается предусмотреть однозначность выводов. Указывается на важность следования альтернативным правилам: либо "размножением" решений сводить сеть к однослойной, либо при ее трассировке строго соблюдать скобочную структуру логических функций, описывающих СПР.
Необходимость популяризации логических нейронных сетей требует вновь, на более высоком уровне, вернуться к рассмотрению и анализу более обобщающих примеров для выработки практических рекомендаций по конструированию логических нейронных сетей и их трассировке. Тем более это необходимо в том случае, если нетерпеливый читатель отвергнет лекцию 1, превращающую, на его взгляд, проблему в "темную и запутанную".
Пусть гипотетическая СПР контролера электропоезда основана на следующих высказываниях:
Х1 = "пассажир предъявил билет"; Х2 = "пассажир не предъявил билет"; Х3 = "в билете указана дата (число) этого дня"; Х4 = "в билете указана дата (число) не этого дня"; Х5 = "в билете указан текущий месяц"; Х6 = "в билете указан не текущий месяц"; Х7 = "в билете указан текущий год"; Х8 = "в билете указан прошлый год"; Х9 = "в билете указан более ранний год"; Х10 = "предъявлены проездные документы работника МПС"; Х11 = "предъявлено пенсионное удостоверение"; Х12 = "не предъявлено пенсионное удостоверение"; Х13 = "предъявлено удостоверение работника МПС"; Х14 = "не предъявлено удостоверение работника МПС"; Х15 = "предложена взятка".
Принимаемые решения:
R1 = "поблагодарить и извиниться за беспокойство"; R2 = "взыскать штраф 100 рублей"; R3 = "взыскать штраф 300 рублей"; R4 = "вызвать милицию"; R5 = "пожурить".
Зададим логическое описание СПР:
 | (9.1) |

Именно возможная неполнота данных обусловливает применение ассоциативного мышления, моделируемого нейросетью.
Не ограничивая общности рассуждений, будем считать, что каждая логическая функция Fi , i = 1, …, S, представляет собой дизъюнктивную нормальную форму (ДНФ) в смысле [22], т.е. имеет вид дизъюнкции конъюнкций, где количество членов, составляющих различные конъюнкции, может быть различным.
Отметим, что традиционно в схемотехнике за ДНФ принимают так называемую совершенную ДНФ (СДНФ), формируемую по известному [22] правилу построения на основе таблицы значений. В ней все конъюнкции имеют одинаковую длину, и их составляют одни переменные в совокупности с отрицанием других.
Однако заведомо излишне учитывать в каждой ситуации, например, предложена взятка или нет. Таким образом, ДНФ, как исходная форма представления, вполне достаточна для полного описания СПР.
Более того, при корректном описании СПР не используется операция отрицания, так как применяются лишь исчерпывающие множества событий (здесь читателю все же придется обратиться к лекции 1). Действительно, отрицание некоторого события равно дизъюнкции остальных событий того же множества. Так, в нашем примере для исчерпывающего множества событий Х1 и Х2 справедливо равенство Х2 =Xi.
Граф-схема выполнения системы логических выражений (9.2), т.е. логическая схема (И-ИЛИ сеть по терминологии [25]) представлена на рис. 9.15. (Не следует пока обращать внимание на веса и пороги.)
Пусть вершины 1-11 этого графа соответствуют логическим элементам - конъюнкторам, а вершины R1-R5 - дизъюнкторам. Тогда построенная схема отображает функционально законченное устройство, реализующее таблицу, с помощью которой контролер осуществляет свои действия. А именно, задавая на входе значения булевых переменных, характеризующие ситуацию, он на одном из выходов хочет получить булево значение "1", указывающее на принимаемое решение. (Далее мы обнаружим ошибку.)

Рис. 9.15. Логическая схема СПР - структура обученной нейросети
Однако предлагаемый табличный метод обусловлен не только тем, что данная задача относится к типу трудно формализуемых задач, т.е. задач, для которых нетипично строгое математическое описание, влекущее построение конструктивных алгоритмов вычисления. Главным образом СПР характеризуется не столько отсутствием математических зависимостей между ее составляющими, сколько недостоверностью данных, противоречивостью информации, работой в условиях помех и т.д. В этом случае СПР реализует модель ассоциативного мышления, которая по неполной, недостоверной, "зашумленной" информации должна выдать ответ на вопрос "На что более похожа ситуация и какое решение наиболее правильно?"
Таким образом, рассмотренная реализация табличного метода, предусматривающего точное задание данных о складывающейся ситуации по принципу "да - нет", должна распространяться на случай неполных, недостоверных данных.
Это означает, что система, отображенная графом на рис. 9.15, должна работать не с булевыми переменными на входе, а с действительными, смысл которых основан на достоверности, вероятности принадлежности (интервалу, значению и др.), экспертной оценке и т.д. Таким образом, должна использоваться не точная информация о ситуации на входе создаваемой СПР, а лишь оценки этой информации. Это было отмечено в предыдущих лекциях.
Зададим логическое описание СПР:
 | (9.1) |

Именно возможная неполнота данных обусловливает применение ассоциативного мышления, моделируемого нейросетью.
Не ограничивая общности рассуждений, будем считать, что каждая логическая функция Fi , i = 1, …, S, представляет собой дизъюнктивную нормальную форму (ДНФ) в смысле [22], т.е. имеет вид дизъюнкции конъюнкций, где количество членов, составляющих различные конъюнкции, может быть различным.
Отметим, что традиционно в схемотехнике за ДНФ принимают так называемую совершенную ДНФ (СДНФ), формируемую по известному [22] правилу построения на основе таблицы значений. В ней все конъюнкции имеют одинаковую длину, и их составляют одни переменные в совокупности с отрицанием других.
Однако заведомо излишне учитывать в каждой ситуации, например, предложена взятка или нет. Таким образом, ДНФ, как исходная форма представления, вполне достаточна для полного описания СПР.
Более того, при корректном описании СПР не используется операция отрицания, так как применяются лишь исчерпывающие множества событий (здесь читателю все же придется обратиться к лекции 1). Действительно, отрицание некоторого события равно дизъюнкции остальных событий того же множества. Так, в нашем примере для исчерпывающего множества событий Х1 и Х2 справедливо равенство Х2 =Xi.
Граф-схема выполнения системы логических выражений (9.2), т.е. логическая схема (И-ИЛИ сеть по терминологии [25]) представлена на рис. 9.15. (Не следует пока обращать внимание на веса и пороги.)
Пусть вершины 1-11 этого графа соответствуют логическим элементам - конъюнкторам, а вершины R1-R5 - дизъюнкторам. Тогда построенная схема отображает функционально законченное устройство, реализующее таблицу, с помощью которой контролер осуществляет свои действия. А именно, задавая на входе значения булевых переменных, характеризующие ситуацию, он на одном из выходов хочет получить булево значение "1", указывающее на принимаемое решение. (Далее мы обнаружим ошибку.)

Рис. 9.15. Логическая схема СПР - структура обученной нейросети
Однако предлагаемый табличный метод обусловлен не только тем, что данная задача относится к типу трудно формализуемых задач, т.е. задач, для которых нетипично строгое математическое описание, влекущее построение конструктивных алгоритмов вычисления. Главным образом СПР характеризуется не столько отсутствием математических зависимостей между ее составляющими, сколько недостоверностью данных, противоречивостью информации, работой в условиях помех и т.д. В этом случае СПР реализует модель ассоциативного мышления, которая по неполной, недостоверной, "зашумленной" информации должна выдать ответ на вопрос "На что более похожа ситуация и какое решение наиболее правильно?"
Таким образом, рассмотренная реализация табличного метода, предусматривающего точное задание данных о складывающейся ситуации по принципу "да - нет", должна распространяться на случай неполных, недостоверных данных.
Это означает, что система, отображенная графом на рис. 9.15, должна работать не с булевыми переменными на входе, а с действительными, смысл которых основан на достоверности, вероятности принадлежности (интервалу, значению и др.), экспертной оценке и т.д. Таким образом, должна использоваться не точная информация о ситуации на входе создаваемой СПР, а лишь оценки этой информации. Это было отмечено в предыдущих лекциях.
Отметим, что в "грамотно" построенной системе такие оценки могут быть вероятностными, являющимися оценками достоверности. Однако принципиально допустима и недостаточная грамотность пользователя. Например, он может быть не осведомлен о понятии исчерпывающего множества событий. Главное, чтобы оценки были относительными, отображающими принцип "больше - меньше" (аналогично экспертным системам), т.к. этого достаточно для моделирования ассоциативного мышления.
Однако конъюнкторы и дизъюнкторы определены лишь для булевых переменных. Следовательно, они должны быть заменены некоторым универсальным элементом, реализующим суррогат этих операций - передаточной функцией, способной на логическом уровне осуществлять схожую реакцию на сигналы на ее входе для получения оценочного сигнала на выходе.
Это и привело к моделированию нейрона - основного логического элемента мозга, к воспроизведению искусственного интеллекта, одним из основных принципов которого является ассоциативное мышление.
На основе логической схемы (рис. 9.15) построим нейронную сеть той же структуры, обученную для решения нашей задачи. Вершины Х1-Х15 соответствуют нейронам-рецепторам входного слоя. От булевых значений их возбуждения перейдем к действительным - к оценкам достоверности соответствующих высказываний ("грамотный" вариант). Эти значения задаются пользователем скорее по наитию, "на глазок", на основе опыта.
Каждая конъюнкция высказываний в записи логических функций (9.1), т.е. совокупность событий, определяет ситуацию. Ситуация является эталоном (эталонной ситуацией), если все составляющие ее события обладают достоверностью, равной единице. В логической схеме каждой конъюнкции соответствует вершина из множества {1, …, 11}. В нейронной сети эти вершины обозначают нейроны промежуточного или скрытого слоя. Нейроны R1-R5 образуют выходной слой; их возбуждение указывает на принимаемое решение.
Как говорилось выше, нейроны рецепторного слоя возбуждаются пользователем, задающим предполагаемую вероятность (или другую оценку) соответствующего события. Остальные нейроны реализуют передаточную функцию таким образом, чтобы возбуждение нейронов-рецепторов распространялось по сети в соответствии со связями. А именно, если, например, на входе сформирован высокий уровень возбуждения нейронов Х1, Х4, Х7 по сравнению с возбуждением других нейронов-рецепторов, то большая величина возбуждения нейрона 2 должна обеспечить самое высокое возбуждение нейрона R2 среди всех нейронов R1-R5 выходного слоя.
Отметим, что таким образом мы пытаемся построить уже обученную нейросеть, где по всем эталонным ситуациям максимального возбуждения должны достигать те нейроны выходного слоя, которые ответственны за решения, соответствующие этим ситуациям. Таким образом, реализуется таблица, о которой говорилось выше.Если же с помощью достоверности событий задавать на входе ситуации, явно не существующие, то нельзя гарантировать правильный ответ. Например, если достоверность всех событий Х1 - Х7 положить равной единице, то столь же бессмысленно будет распределение возбуждения нейронов выходного слоя. Или, если предположить, что мятая бумажка является предъявленным билетом с достоверностью 0,1 (событие Х1), то полагать высоким значение достоверности события Х8 не следует, т.к. эта достоверность является условной вероятностью, и т.д.
То есть логика мышления пользователя и знание элементов теории вероятности должны возобладать.
Выбор передаточной функции
Выбор передаточной функции остается творческой проблемой, во многом определяемой решаемой задачей. Важно лишь то, что полное копирование нейрона, созданного природой, излишне. В то же время передаточная функция - пороговая функция, активно использующая значение порога h.
В нейронных сетях учитывают веса связей - синапсические веса ?. Рассмотрение этих весов актуально, если структура сети первоначально задана и следует ее приспособить (обучить) для решения данной задачи. Пока мы рассматриваем построение уже обученной нейросети, поэтому вес сформированных связей принимаем равным единице. Однако далее будет показано, что корректировка весов необходима даже при построении обученных сетей. Эти веса могут быть скорректированы и в процессе эксплуатации для учета влияния событий на результат - принимаемое решение.
При выборе передаточной функции и порога h руководствуются следующими требованиями:
эти функции в области преодоления порога должны монотонно возрастать по каждому сигналу на входе нейрона;не должно быть "угасания" сигнала возбуждения при его прохождении по сети;сигналы возбуждения на выходном слое должны быть четко различимы по величине для различных эталонных ситуаций;должен быть примерно равным диапазон изменения величин возбуждения нейронов выходного слоя, закрепленных за разными решениями.
Практически, для логического решения задач, достаточно применять одну из следующих, например, используемых в [7], передаточных функций, определяющих величину V возбуждения нейрона в зависимости от величин Vi возбуждения связанных с ним нейронов, весов ? i этих связей, а также порога h:
1.

2.

3.

4.

5.

Поясним последнее требование к передаточной функции. Оно отражает, например, распознавание букв и знаков препинания. При этом целесообразно использовать передаточную функцию 3. Однако распознавание, например, запятой и буквы "А" приводит к резкому различию величин возбуждения соответствующих нейронов выходного слоя. При условии "шумов" запятая становится практически неразличимой, что приводит к необходимости преобразования величин возбуждения нейронов выходного слоя в единый диапазон изменения. Это либо достигается вводом в рассмотрение коэффициентов приведения, как в разделе 4.3, - для одинаковой коррекции всех весов связей каждого нейрона выходного слоя, либо приходится решать эту проблему отдельно для каждой связи такого нейрона, как будет показано далее. В рассматриваемом примере проблема уравнивания сигналов на выходном слое для различных эталонов также актуальна.
Таким образом, выбор и модификация передаточной функции производятся экспериментально, хотя легко установить общие черты функций, рекомендуемых здесь.
"Железнодорожная рулетка"
Как показывает опыт пропагандирования нейросетевых технологий, молодежь слабо воспринимает материал, заставляя лектора каждый раз начинать с пояснения "на пальцах", что собой представляет нейросеть на абстрактном уровне и как она работает. Опасаясь, что наши пространные рассуждения выше отвратили нетерпеливого читателя, но надеясь, что он все же хочет выявить рациональное зерно, мы решили по случаю еще раз на примитивном уровне продемонстрировать подход, поймав читателя в ловушку и заставив его понять самый простой изначальный принцип.
Одновременно необходимо выявить ряд проблем, указывающих на то, что в предыдущих лекциях в области построения систем принятия решений сделано не все.
Построение обученной нейросети. Рассмотрим увлекательную детскую игру - "железнодорожную рулетку", - основанную на так хорошо знакомой вам задаче о встрече. Помните: "Из пунктов А и В навстречу друг другу…" и т.д.?

Рис. 9.1. Железнодорожная рулетка
Начальник станции Кукуевка (старший) и начальник станции Пырловка одновременно выпускают навстречу друг другу два паровоза (рис. 9.1) со скоростью либо 60, либо 80 км/ч. Длина перегона составляет 4 км. Небольшой нюанс заключается в том, что пути перегона то сходятся в один, на протяжении одного километра, то расходятся. И тогда, в зависимости от точки встречи, со станции Кукуевка надо выслать на соответствующий километр либо линейного - даму с приветственным платочком, либо линейного с подстилочной соломкой.
Решение о такой посылке усложняется помехами в линии передачи данных, в связи с чем скорости паровозов сообщаются с достоверностью, меньшей единицы. Кроме того, необходимо каждый эксперимент связать с ожидаемыми денежными затратами на единовременную добавку к пенсии линейных.
В отличие от вас, начальник станции Кукуевка неважно учился в пятом классе, и решать оперативно подобную задачу, да еще при дополнительных условиях, не в состоянии. Он просит о помощи вас, предоставив в ваше распоряжение плохонький компьютер, отказанный в порядке шефской помощи Кукуевской начальной школой.
Он объясняет вам, что не хочет считать вообще, а хочет добиться определенности по принципу "если …, то …", а в случае недостоверных данных - "на что это более всего похоже и что делать?".
Тогда вы понимаете, что без элементов искусственного интеллекта не обойтись. Стимулируя свою изобретательность кружкой пива "Красный Восток", вы ищете что-то похожее на табличный метод, но с автоматической интерполяцией, что-то связанное с ассоциативным мышлением… И вы решаетесь…
Произведем предварительные расчеты, чтобы представить себе все варианты будущего поведения нашей системы принятия решений - для ее обучения. Представим (рис. 9.2) графически структуру логического функционирования создаваемой системы принятия решений.
Кукуевский паровоз имеет скорость 60 км/ч (Событие А1). Пырловский паровоз имеет скорость 60 км/ч (Событие В1). Одновременное выполнение этих событий обозначим А1&В1. Тогда точка встречи находится как раз посредине перегона, что, скорее всего, требует помощи линейного с соломкой. Но возможно и везение за счет неточного определения скоростей. Тогда на всякий случай потребуется дама с платочком. Принимаемое решение, заключающееся в отправлении обоих линейных на границу второго и третьего километров, назовем решением R1. С ним связаны расходы на единовременное пособие М1.

Рис. 9.2. Система принятия решений
Кукуевский паровоз имеет скорость 60 км/ч (Событие А1), но пырловский паровоз имеет скорость 80 км/ч (Событие В2). (Выполняется условие А1&В2.) Тогда их точка встречи находится на втором километре пути, и, следовательно, требует решения R2: "Отправить даму с платочком на второй километр!" В активе указанной дамы появляется сумма М2 условных единиц.Кукуевский паровоз имеет скорость 80 км/ч (Событие А2), пырловский паровоз имеет скорость 60 км/ч (Событие В1). (Выполняется условие А2&В1.) Тогда их точка встречи находится на третьем километре пути, что требует сочувственного вмешательства линейного с соломкой (решение R3), с оплатой труда в М3 условных единиц.Кукуевский и пырловский паровозы имеют скорость 80 км/ч (Событие А2&В2), что ввиду высокой скорости перемещения линейных требует решения R4 с затратами М4.
А теперь оживим эту структуру, заставим ее действовать, как, по-видимому, на логическом уровне действуют структуры нашего мозга.
Представим себе, что на месте каждого овала (потом - кружочка, на рис. 9.2 справа) действует нейроподобный элемент (просто нейрон). Нейроны входного слоя - рецепторы - приходят в возбужденное состояние (подобно сетчатке глаза) в соответствии с той ситуацией, которую мы задаем на входе системы. Например, мы хотим испытать ситуацию А1&В2. Тогда мы полагаем величины возбуждения нейронов А1 и В2 равными единице и записываем VA1 = VB2 = 1. При этом мы не забываем позаботиться о том, чтобы величины возбуждений нейронов А2 и В1 остались равными нулю.
Подчеркнем тот факт, что возбуждение нейронов-рецепторов осуществляется в результате ввода информации.
Для других нейронов, "принимающих" возбуждение в соответствии со стрелками, введем передаточную функцию, в результате выполнения которой формируется величина V возбуждения каждого нейрона. Для нашего случая, недолго думая (ибо существует большой произвол в выборе вида передаточной функции, на любой вкус), определим вид такой функции:

где i - индекс нейрона, "передающего" свое возбуждение данному нейрону, h - порог.
(Напомним: функция ?(x) заменяет отрицательную величину нулем, т.е.

В нашем случае стрелки со всей определенностью указывают направление передачи возбуждений.
Положим h = 1 и рассчитаем величины возбуждения нейронов выходного слоя R1-R4 для ситуации А1&В2:

Таким образом, "высветилось" то решение, которое необходимо принять, и старт линейным должен быть дан. Проверим, что так же работает наша сеть по всем эталонам, по которым мы ее обучили, проложив "проводочки" от каждой исходной посылки к следствию.
Например, в результате искажения информации начальник станции Кукуевка принял решение считать скорость пырловского паровоза равной не то 60, не то 80 км/ч. Но скорее всего - 60! И подойдя к компьютеру, он по наитию набирает: А1 = 1, В1 = 0,7, В2 = 0,4. На какую ситуацию это указывает, и какое решение наиболее правильно? Считаем:

Мы видим, что максимальной величины возбуждения достиг нейрон R1, определивший главное решение. Но мы вправе учесть и решение R2 с меньшим приоритетом, дав даме с платочком дополнительные указания. И в этом проявится наша мудрость. По известной формуле мы можем оценить математическое ожидание того, на сколько облегчится карман начальника Кукуевской станции:

Мы очень просто сформировали уже обученную нейросеть. Однако критический взгляд читателя замечает явные "проколы" и выражает недоумение. Ведь ранее мы говорили о большем! Что ж, подойдем к этому постепенно…
А что, если бы мы захотели объединить решения R1 и R4, отличающиеся (для нас) только скоростью передвижения линейных? Следуя тому же принципу формирования, мы получили бы сеть как на рис. 9.3.
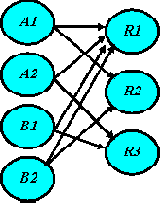
Рис. 9.3. Непригодность однослойной нейросети
Легко видеть, что решение R1 максимально возбуждается всегда, когда мы задаем ситуацию, требующую той же величины максимального возбуждения только лишь нейронов R2 и R3. Сеть как бы дает "побочный эффект". Необходим дополнительный инструктаж пользователя. Он заключается в том, что если максимально и одинаково возбудились два нейрона выходного слоя и один из них R1, то "верить" надо второму. Если максимально возбудился только нейрон R1, то он и выдает правильное решение.
В данном случае произошла коллизия при огульной замене операций конъюнкции



Именно это и наводит на предположение (гипотезу) о минимальной длине статической цепочки, которая рассматривается в разделе 1.9.
По-видимому, нейросеть будет работать правильно, если ее структура полностью воспроизведет структуру указанного логического выражения. Но для этого нейросеть должна быть двухслойной! Более того, глубокий анализ показывает, что обобщенный эталон А1, А2, В1, В2, приводящий к одному решению (R1), поглотил обобщенные эталоны (например, А1, В2), приводящие к другому решению. О какой же однозначности выводов можно говорить!
Тогда легко восстановить справедливость, построив (обученную!) нейросеть так, как показано на рис. 9.4, введя в рассмотрение т.н. "скрытые" нейроны 1 и 2.

Рис. 9.4. "Правильная" обученная нейросеть
Выбор нейросети, обучение-трассировка. Мы построили нейросеть, пользуясь приемами, известными специалистам-схемотехникам, конструирующим устройства компьютера. Мы соединили элементы связями-"проводочками", произведя трассировку, для правильного распространения сигнала в соответствии с замысленной функцией. Мы неоднократно указывали выше, что так мы строим уже обученную сеть. При этом мы полностью исключили из рассмотрения тот параметр, настройка которого позволяет обучить сеть, в частности - проложить нужные "проводочки" и перекусить ненужные.
Нейрон только умеет выполнять передаточную функцию, один из видов которой мы рассмотрели. Но более полная модель нейрона заключается в следующем: нейрон имеет несколько входов - дендритов, каждый из которых обладает весом синапсической связи. В результате выполнения передаточной функции возбуждение нейрона через ветвящийся аксон передается дендритам других нейронов, с которыми связан этот. Дендрит воспринимает сигнал, умноженный на свой вес! Таким образом нейроны и образуют сеть, в которой различаются входной и выходной слои. Передаточная же функция, с учетом синапсических весов, для нашего простейшего случая (при компьютерном моделировании чаще всего другого и не требуется) имеет вид

где Vi - величины возбуждения тех нейронов, аксоны которых связаны с дендритами данного нейрона, i - индекс использованного дендрита, ?i - вес синапсической связи.
И вот весь фокус в построении и в обучении нейросети заключается в том, что синапсические веса регулируются, обусловливая пути прохождения возбуждений в сети!
В частности, представив некоторую абстрактную сеть, мы, построив на ее основе сеть для игры в рулетку, положили некоторые веса связей равными единице (утвердив существование "проводочков"), а некоторые (или все другие) - равными нулю (что соответствует отсутствию "проводочков"). Но ведь можно допустить и некоторые промежуточные значения весов, хотя в практических целях можно поступать так, как поступили мы.
Подойдем иначе к построению нейросети для игры в "железнодорожную рулетку". Ранее нам были известны условия игры, а мы создали сеть. Теперь пусть нам задана нейросеть, а мы обучим ее для игры в рулетку.
Итак, по сошедшему вдохновению мы нарисовали некоторый ориентированный ациклический граф (рис. 9.5) и намерены вложить в него смысл нейросети, поставив в соответствие его вершинам-нейронам (кроме предполагаемых рецепторов) все ту же передаточную функцию.

Рис. 9.5. Нейросеть, предложенная для обучения
Вот только каким способом заставить сеть так реагировать на очевидные эталоны, чтобы максимального возбуждения достигали нейроны выходного слоя, соответствующие решениям? Для этого необходимо, полагая первоначально все веса нулевыми (или минимальными), увеличить некоторые веса, довести до максимального значения или до единицы. Проще всего именно так и действовать: сначала все веса нулевые (хоть "проводочки" есть, их сопротивление чрезвычайно высоко). Затем некоторые веса (и наша задача выбрать, какие) мы полагаем равными единице. Это и будет равносильно тому, что какие-то "проводочки" мы оставим, а какие-то перекусим. Это действие по обучению нейросети мы называем трассировкой.
Продемонстрируем алгоритм трассировки, введя, по сравнению с рассмотренным в лекции 4, некоторые упрощения.
Компьютерная обработка нейросети значительно упрощается, если сеть представлена матрицей следования S (рис. 9.6), где наличие связи обозначается ее весом.

Рис. 9.6. Матрица следования
Произведем трассировку возбуждений нейронов {A1, B1}

Исключим из матрицы S строки и столбцы, соответствующие не интересующим нас нейронам входного и выходного слоев. Матрица примет вид S1 на рис. 9.7.

Рис. 9.7. Матрица следования для трассировки первого решения
Моделируем прохождение возбуждения следующим образом.
Присвоим нейронам, соответствующим нулевым строкам - входам матрицы S1 признак "возбужден". Выделим столбцы, соответствующие этим входам. В совокупности этих столбцов найдем первую строку, содержащую максимальное число нулей. Эта строка соответствует нейрону 1. Заменяем нули единицами (увеличиваем веса), введенные изменения отражаем в матрице S. К матрице S присоединяем столбец (чтобы не отягощать пример, мы этого не сделали, но учитываем его наличие в последующих построениях), в каждой позиции которого указывается число введенных единиц в строке. В данном случае в строке этого столбца, соответствующей нейрону 1, записываем т1 = 2. Это необходимо для возможности "переиспользования" нейронов при получении других решений. Исключаем из матрицы S1 строки и столбцы, "передавшие" свое возбуждение. Нейрону 1 присваиваем признак "возбужден". Матрица S1 принимает вид на рис. 9.8.

Рис. 9.8. Шаг преобразования матрицы следования
Исключаем из матрицы S1 строки и столбцы, соответствующие входам, не отмеченным признаком "возбужден". Эти строки соответствуют нейронам 2 и 3. Матрица S1 принимает вид как на рис. 9.9.

Рис. 9.9. Шаг преобразования матрицы следования
Повторяем очевидные действия, уже описанные выше, что приводит к замене единицей единственного нуля.
Не приводя промежуточного рисунка, отметим, что мы подтвердили высоким весом (единичным) связи А1



Произведем трассировку {A1, B2}

Сформируем матрицу S2, исключив из рассмотрения нейроны A2, B1, R1, R3, R4 (рис. 9.10).

Рис. 9.10. Матрица следования для трассировки второго решения
Строка, соответствующая нейрону 1, содержит одну единицу при том, что т1 = 2. Исключаем из рассмотрения и этот нейрон, как не годный к переиспользованию. Матрица S2 принимает вид как на рис. 9.11.

Рис. 9.11. Шаг преобразования матрицы следования
(Для краткости изложения мы не рассматриваем транзитивные связи, легко вводящиеся в матрицу следования. Тогда мы могли бы исключить из рассмотрения нейрон 3, так как нет связи 3

Присваиваем строкам, соответствующим входам матрицы S2, признак "возбужден". Находим в совокупности соответствующих им столбцов строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 2. Заменяем в ней нули единицами, что отмечаем в матрице S. Полагаем т2 = 2. Присваиваем нейрону 2 признак "возбужден", а нейроны А1 и В2 исключаем из рассмотрения. Среди оставшихся строк оказывается "пустая" строка, которая соответствуюет нейрону 3, не обладающему признаком "возбужден". Исключаем и ее, вместе с соответствующим столбцом. Матрица S2 принимает вид как на рис. 9.12.

Рис. 9.12. Шаг преобразования матрицы следования
Повторение очевидных действий приводит к замене оставшегося нуля единицей.
Таким образом, в результате трассировки на данном шаге сложились связи с единичными весами A1



Повторив схему построений, легко найдем связи с единичными весами A2




А вот трассировка последнего пути возбуждения, {A2, B2}

Сформируем матрицу S4, свободную от представительства тех нейронов, в строках которых число единиц меньше соответствующего значения т. Такая матрица показана на рис. 9.13. Но ведь никаких связей в ней нет вообще!

Рис. 9.13. Матрица следования для трассировки четвертого решения
Придется их ввести, да еще с единичными весами. Ведь мы готовы создавать нужную нам сеть, а не обязаны приспосабливаться. Да и что мы можем сделать - только отвергнуть эту сеть и искать новую? Мы видим, что больше трех эталонов эта сеть все равно не способна воспринять. Таким образом, мы вводим дополнительные связи с единичными весами A2


Окончательно обученная сеть представлена на рис. 9.14, где выделены связи с единичными весами. (Другие "проводочки" мы могли бы перекусить.)

Рис. 9.14. Обученная нейросеть
Но радоваться рано. Посчитаем с помощью нашей передаточной функции величины возбуждения нейронов для, например, ситуации A1&B2: V1 = 0, V2 = 1, V3 = 0, VR1 = 0, VR2 = 0, VR3 = 0, VR4 = 0. Ни один нейрон выходного слоя не возбудился! То же - для ситуаций A1&B1 и A2&B1. Рассчитаем ситуацию A2&B2: V1 = 0, V2 = 0, V3 = 0, VR1 = 0, VR2 = 0, VR3 = 0, VR4 = 1. Мы видим, что построенная нейросеть распознает единственную ситуацию.
Анализируя, мы убеждаемся, что в процессе распространения по сети возбуждение "гаснет", не доходя до выходного слоя. Тогда мы начинаем "подкручивать" пороги, уменьшая их. Но тотчас замечаем другую неприятность: величины возбуждения нейронов выходного слоя различны для разных ситуаций, ибо различна длина путей возбуждения. Это затрудняет правильное участие этих нейронов в следующих логических слоях, когда данный выходной слой является входным для следующего логического уровня сети. Мы видим, что наша передаточная функция не годится для выбранной структуры нейросети.
Но мы же располагаем свободой выбора, которая допускает условности, вероятно, нереализованные в природе, находящейся в жестких рамках установленных законов и средств.
Рекомендуем "хорошую" передаточную функцию, определяющую величину V возбуждения нейрона:

Рассчитайте и убедитесь, что, например, для h = 1 сеть правильно распознает все эталонные ситуации, обеспечивая равную величину возбуждения нейронов выходного слоя.Так, при ситуации A1&B1 получаем следующие величины возбуждения нейронов: V1 = 2, V2 = V3 = 0, VR1 = 2, VR2 = VR3 = VR4 = 0. Аналогично - для ситуаций A1&B2 и A2&B1. Для ситуации A2&B2 находим V1 = V2 = V3 = 0, VR1 = VR2 = VR3 = 0, VR4 = 2.
Сеть работает прекрасно, гарантируя правильность реакции на недостоверные ситуации, и позволяя находить среднее.
А главное, сколько прекрасных вариантов развития имеет игра, стимулируя наше предвидение! Например, что, если скорость паровозов - величина переменная и случайная, так же как и чередование и длина однопутных участков, и решение следует принимать и корректировать в динамике, в зависимости от длины пройденного пути и значения скорости? Что, если один машинист охвачен идеей суицида, а другой желает уклониться от столкновения? и т.д. (Бедные линейные!)
Дистрибутивная форма логического описания системы принятия решений
Приведенные выше построения предполагали представление логических выражений, описывающих СПР, в ДНФ. Однако известно, что каждое логическое выражение на основе алгебры высказываний может быть представлено и в виде конъюнктивной нормальной формы (КНФ). Такая форма также приводит к достаточности не более чем двухслойной нейросети. Мы не будем приводить такое представление для анализируемого примера, усложнившее описание СПР, но не приведшее к новым интересным выводам, однако сделаем общее замечание о важности минимизации количества слоев нейронной сети.
Развитие систем принятия решений, таких как медицинская или техническая диагностика, прогнозирование рынка ценных бумаг, управление перевозками железнодорожным транспортом и др., приводит к весьма большому числу исследуемых факторов и, следовательно, к еще большему числу нейронов сети. Расчет для каждого нейрона даже несложной передаточной функции в общем цикле обработки всех нейронов (в соответствии с их частичной упорядоченностью на основе преемственности информации) может привести к значительным временным затратам, ставящим под сомнение оперативность управления.
Необходима "аппаратная поддержка", что породило большое число предложений [14] в области разработки нейрокомпьютеров (НК), реализующих нейросети. В основе НК лежит принцип распараллеливания вычислений, что фактически означает распределение нейронов (программных процедур, моделей нейроподобных элементов и т.д.) между исполнительными вычислительными устройствами – процессорами для их обработки. Эффективны НК, выполненные в виде приставки к персональному компьютеру или рабочей станции. Ориентация НК на обработку универсальной двухслойной нейросети на основе ДНФ жестко распределяет функции слоев и возможные связи его процессоров, используя элементы стандартизации и унификации.
В лекции 1 обсуждалась проблема минимизации длины логической цепочки и было показано, что с помощью "размножения" решений такая длина может быть даже доведена до единичной.
лекцию 1) записывается как

Предполагается возможность такого преобразования произвольной логической функции – композиции операций конъюнкции и дизъюнкции, при котором обеспечивается единственность вхождения каждой переменной в полученную запись. Основная операция, которая при этом используется – вынесение за скобку.
Однако, как следует из примера, рассмотренного в лекции 1, такое преобразование не всегда приводит к успеху. Это свидетельствует о том, что в крайнем случае, для обеспечения единственности вхождения переменных, все же следует прибегать к способу "размножения" решений. Такое вынужденное "размножение" также отнесем к акту дистрибутивного преобразования.
Важность используемого в этом преобразовании свойства дистрибутивности приводит к целесообразности его учета в названии соответствующего логического описания СПР. Полученную таким образом нейросеть справедливо назвать нейросетью на основе дистрибутивного логического описания или просто дистрибутивной.
Упростим описание СПР, воспользовавшись операциями вынесения за скобки и выделения общих выражений:
 | (10.2) |
Форма представления (10.2) не только стала проще, она стала естественнее и понятнее. Однако наличие вложенных скобок вселяет сомнение в возможность использования не более чем двух слоев нейросети.
На рис. 10.2 (пока не следует обращать внимание на веса связей) отображена логическая схема реализации (10.2), она же – дистрибутивная нейросеть. Чтобы "не потерять" информацию, в кружках, обозначающих нейроны, указан тип логической операции прообраза – конъюнктора или дизъюнктора.
Выберем ту же передаточную функцию 3 и проверим, необходима ли здесь коррекция порогов и весов связей. Предварительно отметим, что описание (10.2) затрудняет перебор эталонных ситуаций.
Для удобства их формирования все же воспользуемся аналогичной системой (9.1)-(10.1). Выберем малое значение порога h = 0,3, "не мешающее" суммированию сигналов, и, исключая очевидные вычисления, проанализируем отображение эталонных ситуаций.

Рис. 10.2. Дистрибутивная нейросеть
Анализ показывает, что побочные эффекты отсутствуют. Это легко было предвидеть, т.к. выше их появление объяснялось неоднократным вхождением некоторых переменных–высказываний в одни и те же логические выражения при применении аддитивной передаточной функции.
При корректном задании исходной информации, т.е. при правильно сформулированном запросе на основе "физического смысла" СПР, имитируются функции конъюнкторов и дизъюнкторов – прообразов нейронов. То есть высокий уровень сигнала нейрона, принявшего роль конъюнктора, возникает в том случае, если все его входы предельно возбуждены. Нейроны, принявшие на себя роль дизъюнкторов, могут возбуждаться лишь при максимальном возбуждении одного из входов.
Однако величины возбуждения нейронов выходного слоя различны. Различаются и сигналы, приходящие на один нейрон от разных эталонных ситуаций.
Как и ранее, уточним веса связей нейронов выходного слоя (рис. 10.2). А именно, если нейрон принял роль дизъюнктора, то вес каждой связи уточняется отдельно по величине возбуждения, формируемой на основе соответствующего эталона. Новый вес равен единице, деленной на эту величину.
Если нейрон принял роль конъюнктора, то все веса его связей, до того равные единице, делятся на сумму сигналов, пришедших по всем связям при предъявлении соответствующего эталона, т.е. веса сохраняют одинаковые значения, а величина возбуждения этого нейрона становится равной единице.
Составим табл. 10.2 на основе расчета ситуаций, отображенных в табл. 10.1, и проанализируем ее. По эталонам (представлены не все, остальные легко рассчитать) сеть работает правильно.
По столбцу 8 видим, что сеть высказалась за решение R2. Этому решению следует больше доверять, т.к.
высокое значение порога ранее существенно уменьшало величину распространяемого сигнала. Значение возбуждения R2, превышающее единицу, следует отнести за счет некорректности вопроса: предъявление пенсионного удостоверения или удостоверения работника МПС должно оцениваться исходя из условной вероятности, а именно, при условии, что билет не предъявлен. Таким образом, исходные оценки, подаваемые на рецепторный слой, предполагают структуризацию вопросов.
Столбец 9 демонстрирует довлеющую роль пенсионного удостоверения или удостоверения работника МПС, несмотря на подозрение на взятку, что исключает неоднозначность решения в табл. 10.1.
Столбец 10 свидетельствует о том, что полная неопределенность, следующая из предъявленных проездных документов, наказуема, хотя и малым штрафом.
| 0 | 0 | 0 | 0,25 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 |
| 0,33 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,65 | 0,05 | 0,4 |
| 0,67 | 1 | 1 | 1 | 0 | 0,33 | 0,33 | 1,2 | 0,33 | 1,43 |
| 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,93 | 0,33 | 0,45 |
| 1 | 1 | 1 | 0 | 1 | 2 | 0 | 1 | 0,1 | 0,8 |
| 2 | 3 | 3 | 0 | 0 | 1 | 0 | 2,5 | 0,1 | 1,8 |
| 4 | 2 | 2 | 0 | 0 | 1 | 0 | 3,1 | 0,1 | 1,8 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 1,5 | 0,5 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0,1 | 0,6 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0,1 | 0,5 |
| 0 | 0 | 0 | 3 | 0 | 0 | 1 | 1,1 | 0,9 | 2,5 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0,7 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1,3 | 0 | 1 |
| 2 | 2 | 2 | 0 | 0 | 1 | 0 | 1,8 | 0,1 | 0,8 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Кроме того, известно [6], что эффективность распараллеливания, основным компонентом которой является минимум времени выполнения комплекса частично упорядоченных работ, зависит от длины критического пути в информационном графе, каким отображается нейросеть. Эта длина должна быть минимальной, что и обеспечивается не более чем двумя слоями нейросети. Следовательно, такая сеть гарантирует возможность оптимального распараллеливания.
Подобное заключение известно и специалистам по схемотехнике, всегда стремящимся минимизировать максимальную длину логической цепочки в схеме разрабатываемого устройства, влияющей на длительность такта его работы.
Однако, требуя обязательного представления логических выражений, описывающих СПР, в дизъюнктивной нормальной форме, мы предполагаем скобочную запись, с открытыми относительно операции конъюнкции некоторыми потенциальными скобками. Это, например, приводит к тому, что в выражении (9.1), определяющем решение R2, дважды присутствует конъюнкция Х1

Тогда справедливо предположение о том, что, наоборот, вынесение за скобки способно не только упростить запись, обеспечив единственное вхождение переменных, но и тем самым исключить побочный эффект.
Для этого воспользуемся правилами эквивалентных преобразований. Определяющим в данном применении является симметричное свойство дистрибутивности конъюнкции относительно дизъюнкции и наоборот. (В алгебре применим лишь дистрибутивный, распределительный закон умножения относительно сложения.) Данное свойство (см.
лекцию 1) записывается как

Предполагается возможность такого преобразования произвольной логической функции – композиции операций конъюнкции и дизъюнкции, при котором обеспечивается единственность вхождения каждой переменной в полученную запись. Основная операция, которая при этом используется – вынесение за скобку.
Однако, как следует из примера, рассмотренного в лекции 1, такое преобразование не всегда приводит к успеху. Это свидетельствует о том, что в крайнем случае, для обеспечения единственности вхождения переменных, все же следует прибегать к способу "размножения" решений. Такое вынужденное "размножение" также отнесем к акту дистрибутивного преобразования.
Важность используемого в этом преобразовании свойства дистрибутивности приводит к целесообразности его учета в названии соответствующего логического описания СПР. Полученную таким образом нейросеть справедливо назвать нейросетью на основе дистрибутивного логического описания или просто дистрибутивной.
Упростим описание СПР, воспользовавшись операциями вынесения за скобки и выделения общих выражений:
 | (10.2) |
Форма представления (10.2) не только стала проще, она стала естественнее и понятнее. Однако наличие вложенных скобок вселяет сомнение в возможность использования не более чем двух слоев нейросети.
На рис. 10.2 (пока не следует обращать внимание на веса связей) отображена логическая схема реализации (10.2), она же – дистрибутивная нейросеть. Чтобы "не потерять" информацию, в кружках, обозначающих нейроны, указан тип логической операции прообраза – конъюнктора или дизъюнктора.
Выберем ту же передаточную функцию 3 и проверим, необходима ли здесь коррекция порогов и весов связей. Предварительно отметим, что описание (10.2) затрудняет перебор эталонных ситуаций.
Для удобства их формирования все же воспользуемся аналогичной системой (9.1)-(10.1). Выберем малое значение порога h = 0,3, "не мешающее" суммированию сигналов, и, исключая очевидные вычисления, проанализируем отображение эталонных ситуаций.

Рис. 10.2. Дистрибутивная нейросеть
Анализ показывает, что побочные эффекты отсутствуют. Это легко было предвидеть, т.к. выше их появление объяснялось неоднократным вхождением некоторых переменных–высказываний в одни и те же логические выражения при применении аддитивной передаточной функции.
При корректном задании исходной информации, т.е. при правильно сформулированном запросе на основе "физического смысла" СПР, имитируются функции конъюнкторов и дизъюнкторов – прообразов нейронов. То есть высокий уровень сигнала нейрона, принявшего роль конъюнктора, возникает в том случае, если все его входы предельно возбуждены. Нейроны, принявшие на себя роль дизъюнкторов, могут возбуждаться лишь при максимальном возбуждении одного из входов.
Однако величины возбуждения нейронов выходного слоя различны. Различаются и сигналы, приходящие на один нейрон от разных эталонных ситуаций.
Как и ранее, уточним веса связей нейронов выходного слоя (рис. 10.2). А именно, если нейрон принял роль дизъюнктора, то вес каждой связи уточняется отдельно по величине возбуждения, формируемой на основе соответствующего эталона. Новый вес равен единице, деленной на эту величину.
Если нейрон принял роль конъюнктора, то все веса его связей, до того равные единице, делятся на сумму сигналов, пришедших по всем связям при предъявлении соответствующего эталона, т.е. веса сохраняют одинаковые значения, а величина возбуждения этого нейрона становится равной единице.
Составим табл. 10.2 на основе расчета ситуаций, отображенных в табл. 10.1, и проанализируем ее. По эталонам (представлены не все, остальные легко рассчитать) сеть работает правильно.
По столбцу 8 видим, что сеть высказалась за решение R2. Этому решению следует больше доверять, т.к.
высокое значение порога ранее существенно уменьшало величину распространяемого сигнала. Значение возбуждения R2, превышающее единицу, следует отнести за счет некорректности вопроса: предъявление пенсионного удостоверения или удостоверения работника МПС должно оцениваться исходя из условной вероятности, а именно, при условии, что билет не предъявлен. Таким образом, исходные оценки, подаваемые на рецепторный слой, предполагают структуризацию вопросов.
Столбец 9 демонстрирует довлеющую роль пенсионного удостоверения или удостоверения работника МПС, несмотря на подозрение на взятку, что исключает неоднозначность решения в табл. 10.1.
Столбец 10 свидетельствует о том, что полная неопределенность, следующая из предъявленных проездных документов, наказуема, хотя и малым штрафом.
| 0 | 0 | 0 | 0,25 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 |
| 0,33 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,65 | 0,05 | 0,4 |
| 0,67 | 1 | 1 | 1 | 0 | 0,33 | 0,33 | 1,2 | 0,33 | 1,43 |
| 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,93 | 0,33 | 0,45 |
| 1 | 1 | 1 | 0 | 1 | 2 | 0 | 1 | 0,1 | 0,8 |
| 2 | 3 | 3 | 0 | 0 | 1 | 0 | 2,5 | 0,1 | 1,8 |
| 4 | 2 | 2 | 0 | 0 | 1 | 0 | 3,1 | 0,1 | 1,8 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 1,5 | 0,5 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0,1 | 0,6 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0,1 | 0,5 |
| 0 | 0 | 0 | 3 | 0 | 0 | 1 | 1,1 | 0,9 | 2,5 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0,7 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1,3 | 0 | 1 |
| 2 | 2 | 2 | 0 | 0 | 1 | 0 | 1,8 | 0,1 | 0,8 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Корректировка порогов
В лекции 2 показано, что при моделировании конъюнктора с помощью нейрона для того, чтобы этот нейрон приходил в возбужденное состояние только после прихода сигналов возбуждения от всех связанных с ним нейронов, необходимо задать ему высокое значение порога. Так, рассчитывая на максимальную единичную достоверность (аналог булевой единицы) высказываний, считаем, что нейрон 1 должен прийти в возбужденное состояние, если Х1 = Х3 = Х5 = Х7 = 1, т.е. предъявлен соответствующий эталон. Это возможно, если порог h1 превышает значение 3, равное уменьшенному на единицу числу возбуждаемых входов. Однако этот порог должен быть преодолен и в том случае (а это и является достоинством нейросети), если отдельные события, составляющие ситуацию, появляются с достоверностью, меньшей единицы. В этом случае необходимо так подобрать пороги для всех нейронов, прообразами которых являются конъюнкторы, чтобы "нужные" нейроны возбуждались, а "побочные эффекты" исключались.
Это требование приводит к важной исходной предпосылке создания нейросети, основанной на понятии существенности события.
На этапе проектирования нейросети выбирается некоторое значение H достоверности. Тогда событие является существенным, если его достоверность не ниже значения H.
Это не означает, что пользователь ограничен значениями предполагаемой достоверности событий, которую он задает на входном слое. Во-первых, в корректно представленной СПР, использующей исчерпывающие множества событий, низкая достоверность одних событий свидетельствует в пользу высокой достоверности других. Во-вторых, значение H – предпочтительная граница достоверности, учитываемая при формировании порога. Более того, это значение может характеризовать лишь среднюю величину возбуждения, подаваемого на один вход нейрона, взявшего на себя роль конъюнктора.
В данном примере, дабы избежать побочного эффекта, необходимо, чтобы нейроны 2 и 3 не возбуждались при высоких значениях Х1 и Х7 в то время, когда высокое значение возбуждения имеют нейроны Х3 и Х5.
Они должны возбуждаться при высоком значении возбуждения нейронов Х4 и Х6. Однако в этом случае нейрон 1 должен возбуждаться лишь при высоком уровне возбуждения нейронов Х3 и Х5.
Учитывая приблизительность и неточность, лежащие в основе имитации ассоциативного мышления с помощью нейросети, необходимо согласиться с эвристическим или экспериментальным выбором порогов , используемых при счете передаточной функции нейронами-конъюнкторами, предоставив лишь рекомендации.
Обозначим ni – количество активных входов нейрона i. Пусть hi = Hni, i = 1, …, 11. Положим H = 0,7. Тогда (рис. 9.15) h1 = 2,8, h2 = h3 = h4 = 2,1, h5 = … = h11 = 1,4.
Рассчитаем значения возбуждения нейронов выходного слоя для ситуаций, отображенных в табл. 10.1, и, в частности, приведших к неоднозначности решения.
Для ситуации 1 имеем V1 = 4 (4 > 2,8), V2 = V3 = 0 (2 < 2,1), V4 = … = V11 = 0, R1 = 4, R2 = … = R5 = 0.
Для ситуации 2 находим V1 = … = V11 = 0, R1 = 1, R2 = … = R5 = 0.
Для ситуации 3 имеем V1 = 0 (2 < 2,8), V2 = 3 (3 > 2,1), V3 = 0 (2 < 2,1), V4 = … = V11 = 0, R1 = 0, R2 = 3, R3 = R4 = R5 = 0.
Ситуация 4: V1 = V2 = V3 = 0, V4 = 3 (3 > 2,1), V5 = … = V11 = 0, R1 = 0, R2 = 3, R3 = R4 = R5 = 0.
Ситуация 5: V1 = … = V5 = 0, V6 = 2 (2 > 1,4), V7 = V11 = 0, R1 = R2 = 0, R3 = 2, R4 = R5 = 0.
Для ситуации 8 имеем V1 = … = V8 = 0, V9 = 2 (2 > 1,4), V10 = V11 = 0, R1 = R2 = R3 = 0, R4 = 2, R5 = 0.
Проверив остальные эталоны, убеждаемся в том, что неоднозначность решения, принимаемого по всем эталонным ситуациям, ликвидирована. (Не появится ли она при последующих действиях?)
Корректировка весов связей нейронов выходного
ДНФ наглядно демонстрирует смысл задачи, так как каждая конъюнкция, включая содержащую единственное высказывание, соответствует отдельной ситуации. Дизъюнкция таких конъюнкций определяет множество ситуаций, приводящих к одному решению. Отсюда, прообразами нейронов выходного слоя являются дизъюнкторы, реализующие операцию ИСКЛЮЧАЮЩЕЕ ИЛИ, т.е. предполагающие анализ не более чем одного единичного сигнала на входе.
Выше было установлено, что при замене логических операций счетом единой передаточной функции даже для эталонных ситуаций возможен побочный эффект, при котором на один нейрон выходного слоя для совместной обработки поступают высокие сигналы возбуждения более чем одного нейрона, т.е. отображающие одновременное наличие разных ситуаций. Это способствует неоднозначности решений.
Показано, что с помощью порогов можно ликвидировать побочный эффект, и мы вправе считать, что высокий сигнал возбуждения, соответствующий действительной ситуации, воспринимается нейроном выходного слоя с единственного входа, что в большей степени адекватно имитируемой логической операции.
Однако величина возбуждения нейронов выходного слоя осталась различной в связи с различной величиной возбуждения нейронов скрытого (промежуточного) слоя.
Введем веса связей (входов) каждого нейрона выходного слоя, равные обратной величине уровня сигнала при предъявлении эталонной ситуации, поступающего на каждый вход. Этим мы добьемся принадлежности величин возбуждения нейронов выходного слоя диапазону [0, 1]. Этот диапазон будет реализован при "грамотном" задании достоверности событий на рецепторном входе.
Выбранный диапазон уравнивает роль входного и выходного слоев в случае, если при создании "длинных" логических цепочек умозаключений реализуется вложенность нейросетей. Это означает, что выходной слой одной нейросети тотчас используется в качестве входного слоя другой.
В исследуемом примере веса связей вводятся на основе анализа величин возбуждения нейронов выходного слоя при рассмотрении всех возможных эталонов, как представленных в табл. 9.1, так и немногих оставшихся.
Полученные веса отображены на рис. 9.15.
Однако после корректировки весов, приведшей к одинаковому, единичному значению возбуждения нейронов выходного слоя в ответ на каждую эталонную ситуацию, вновь замечаем возникшую неоднозначность решения. А именно, высказывание Х10 образует эталонную ситуацию, приводящую к решению R1. В то же время Х10 участвует в создании ситуаций Х8

и Х9

Исследуя пути исправления ошибки, приходим к выводу, что в основе обнаруженной коллизии лежит некорректное описание СПР, необнаруженное противоречие в задании на разработку. Еще на этапе составления логической схемы (рис. 9.15) мы могли обнаружить получение единичных сигналов не на единственном выходе.
Тогда вспоминаем, что бесплатный билет – проездной документ – предъявляется обязательно вместе с удостоверением работника МПС!
Дополним описание (9.1), уточнив логическое выражение для R1:
 | (10.1) |


Рис. 10.1. Нейросеть после уточнения логического описания
В табл. 10.1 представлены результаты расчета принимаемых решений по предъявленным эталонным ситуациям (для проверки правильности) и по ряду неопределенных ситуаций (столбцы 8-10). Анализ таблицы показывает, что решения, принятые нейросетью, вполне объяснимы. Это относится даже к неоднозначному решению (столбец 9).
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,75 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,75 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0,77 | 0 | 0,83 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,87 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1,5 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1,5 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 2,5 |
| 0 | 0 | 3 | 0 | 0 | 0 | 0 | 2,3 | 0 | 0 |
| 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 3,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Полученные веса отображены на рис. 9.15.
Однако после корректировки весов, приведшей к одинаковому, единичному значению возбуждения нейронов выходного слоя в ответ на каждую эталонную ситуацию, вновь замечаем возникшую неоднозначность решения. А именно, высказывание Х10 образует эталонную ситуацию, приводящую к решению R1. В то же время Х10 участвует в создании ситуаций Х8

и Х9

Исследуя пути исправления ошибки, приходим к выводу, что в основе обнаруженной коллизии лежит некорректное описание СПР, необнаруженное противоречие в задании на разработку. Еще на этапе составления логической схемы (рис. 9.15) мы могли обнаружить получение единичных сигналов не на единственном выходе.
Тогда вспоминаем, что бесплатный билет – проездной документ – предъявляется обязательно вместе с удостоверением работника МПС!
Дополним описание (9.1), уточнив логическое выражение для R1:
 | (10.1) |


Рис. 10.1. Нейросеть после уточнения логического описания
В табл. 10.1 представлены результаты расчета принимаемых решений по предъявленным эталонным ситуациям (для проверки правильности) и по ряду неопределенных ситуаций (столбцы 8-10). Анализ таблицы показывает, что решения, принятые нейросетью, вполне объяснимы. Это относится даже к неоднозначному решению (столбец 9).
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,75 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,75 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0,77 | 0 | 0,83 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,87 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1,5 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1,5 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 2,5 |
| 0 | 0 | 3 | 0 | 0 | 0 | 0 | 2,3 | 0 | 0 |
| 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 3,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Корректное задание исходных данных – условие правильности выводов нейросети
Ранее не раз говорилось о "грамотном" задании исходных данных для адекватной реакции нейросети. Опыт пользователя должен развиваться на основе понимания логической и вероятностной взаимосвязей событий, являющихся предметом ее исследований. Необоснованное, случайное задание достоверности высказываний может привести лишь к утверждению известной шутки "каков вопрос – таков ответ".
Мы можем предварительно, на основе интуиции, лишь догадываться, что, например, достоверность высказывания "в билете указана дата (число) этого дня" зависит от достоверности высказывания "пассажир предъявил билет".
В лекции 1 для представления структуры взаимосвязанных событий рассматривались деревья логических возможностей (ДЛВ).
Составим дерево логических возможностей, связывающее вероятности событий, которые лежат в основе примера СПР (рис. 10.5), анализируемой в настоящей лекции.
При составлении ДЛВ учитывается, что каждое ветвление на основе некоторого события определяет исчерпывающее множество последующих событий при условии наступления данного. Следовательно, на ребрах (не на всех, чтобы не перегружать рисунок) указаны условные вероятности. Тогда полная вероятность некоторого события отыскивается как сумма произведений вероятностей, которые найдены по всем путям ДЛВ, приводящим к этому событию.
На основе анализа ДЛВ можно получать рекомендуемые диапазоны задания достоверности некоторых высказываний. Например, вероятность Р(Х7) события Х7 (в билете указан текущий год) находится следующим образом:

Для грубой оценки можно считать все элементы даты (число, месяц, год) независимыми и одинаково подверженными искажению. Тогда Р1 3 = Р3 5 = Р4 5 = Р5 7 = Р6 7 = Р, Р1 4 = Р3 6 = Р4 6 = 1 – Р, а Р(Х7) = Р0 1Р.
Если установлено, что в любом билете из-за неразборчивой печати каждый элемент даты обладает достоверностью Р = 0,9, и если, как в столбце 10 табл. 10.2, Х1 = 0,5, то с достаточной точностью можно задать Х3 = Х5 = Х7 = 0,45, Х4 = Х6 = 0,55, Х8 = Х9 = 0,5(1 – 0,45).
Сформулируем вопрос нейросети, задав непредусмотренную эталонную ситуацию Х10 = Х4 = Х6 = 1. Обе нейросети отвечают максимальным возбуждением нейрона R2. Рассчитывая на приблизительность, лежащую в основе ассоциативного мышления, можно вполне удовлетвориться полученным решением.
Однако с учетом предыдущего примера необходимо отметить, что нейросеть "фантазирует" и полагаться на адекватность ее выводов по непредусмотренным ситуациям не следует.
Несомненно, пробегающее по сети возбуждение при предъявлении непредусмотренной ситуации приводит к тому, что некоторый (некоторые) нейрон выходного слоя возбуждается более других, отвечая на вопрос: "на что более всего похожа данная ситуация?" Это так характерно для нашей жизни! Однако аналитический ум не удовлетворяется подобным ответом. Критический подход использует высокое значение порога достоверности на выходном слое.
Повысим значение порогов передаточной функции, реализуемой нейронами выходного слоя, положив их, например, равными 0,7. Тогда обе нейросети не будут реагировать на ситуацию в примере 1. Дистрибутивная нейросеть на рис. 10.2 не реагирует также на предложенную в примере 2 эталонную ситуацию, т.к. величина возбуждения нейрона R2 составляла 0,66. Однако величина возбуждения этого нейрона в однослойной нейросети на рис. 10.3 составляла единицу, что требует дальнейшего повышения порога. Оно же может привести к ликвидации правильной реакции на предусмотренные ситуации. Ведь в столбце 9 табл. 10.2 максимальное возбуждение нейрона выходного слоя, обусловливающее адекватный вывод, составляет всего 0,95.
Если все же предъявленная ситуация "не одолела" предельно повышенный порог на выходном слое, ее следует считать не знакомой нейросети, не похожей ни на что, чему ее учили. Сеть требует вмешательства учителя, обучения новой ситуации.
В случае же возникновения "фантазий", не подвергающихся критическому анализу, можно предусмотреть самообучение нейросети, т.е. трассировку, закрепляющую новую причинно-следственную связь.Это справедливо в том случае, если "работа" нейросети, т.е. принимаемые ею решения, контролируются с помощью критериальной функции, оценивающей функционирование СПР. А именно: если решение, принятое в результате "фантазии", привело к удовлетворительному исходу, оно утверждается, и нейросеть получает разрешение на трассировку нового эталона.
Ветвь ДЛВ, обусловленная событием Х2, не может быть исследована в вероятностном аспекте, т.к., например, предъявление или непредъявление пенсионного удостоверения – свершаемые события, обладающие единичной достоверностью.

увеличить изображение
Рис. 10.5. Дерево логических возможностей
Кроме того, возникает вопрос: почему при предъявлении неэталонных ситуаций величина максимального возбуждения нейронов выходного слоя часто превышает единицу? Ведь проводилась коррекция весов связей этих нейронов. Следует отметить, что на вход нейросети могут подаваться ситуации в самом непредсказуемом совмещении, отличном от идеального задания эталонов. Особенность и цель построения нейросети, как средства ассоциативного мышления, – возможность разобраться в наибольшей похожести. Коррекция весов связей по эталонам гарантирует лишь приблизительный интервал изменения величин возбуждения нейронов выходного слоя.
Таким образом, ДЛВ является вспомогательным средством, рекомендуемым пользователю на этапе обретения опыта, позволяющим учитывать явную зависимость событий и не допускающим абсурдных предпосылок при формировании вопросов нейросети.
Однако составление ДЛВ позволяет не только установить зависимость между достоверностью отдельных высказываний (событий), но и выявить те комбинации событий, т.е. ситуации, которые оказались неучтенными при проектировании СПР.
Пример 1. Что делать, если пассажир предъявил проездные документы, но не предъявил удостоверение работника МПС? Сформулируем вопрос нейросети, задав эталон этой ситуации, т.е. положим Х10 = Х14 = 1 и исследуем реакцию дистрибутивной нейросети на рис. 10.2 и однослойной нейросети на рис. 10.3. В обоих случаях получаем R1 = 0,5, R2 = 0,33, R3 = R4 = 0,5, R5 = 0. Конечно, по данному эталону можно принять одно из рекомендуемых решений R1, R3, R4, тем более что по ситуации, не известной сети, мог максимально возбудиться единственный нейрон выходного слоя, как рассмотрено ниже.
Пример 2. Обнаруживаем, что при логическом описании СПР не учтены все комбинации дат выдачи проездных документов.
Совершенные нейронные сети
В лекции 1 для систем принятия решений введено известное в теории вероятностей понятие исчерпывающего множества событий (высказываний). События (высказывания) образуют исчерпывающее множество, если сумма их вероятностей (достоверностей) равна единице (известное условие нормировки).
При организации СПР это означает обязательный учет всех значений, состояний или возможностей использования каждого фактора. Например, множества {X1, X2}, {X7, X8, X9} – исчерпывающие множества высказываний о событиях. Однако фактор взятки не образует такого множества, как говорилось ранее, – из-за его недостаточной актуальности в формируемой СПР.
Допустим, что для создаваемой СПР, исходя из специализации, по каждому фактору необходимо учитывать все возможные варианты его значений. То есть рассмотрение каждого фактора при построении нейросети приводит к формированию исчерпывающего множества высказываний относительно него.
Далее, пусть каждая ситуация представляется конъюнкцией, в которой обязательно участвуют высказывания относительно всех факторов, по которым формируется нейросеть. Тогда все конъюнкции (ситуации) имеют одинаковое число высказываний.
Пусть любые две отличные друг от друга ситуации приводят к различным решениям. Это означает, что в логическом описании СПР отсутствует операция дизъюнкции. Если, исходя из смысла создаваемой СПР, такая операция предполагается, т.е. неединственная ситуация приводит к одному и тому же решению, то с помощью "размножения" решений, как это было сделано в примере предыдущего раздела, можно добиться исключения операции дизъюнкции.
Нейросеть, в которой каждая исследуемая ситуация имеет постоянное число образующих ее событий (высказываний), отображающих все факторы, и в которой взаимно отличающиеся ситуации приводят к различным решениям, назовем совершенной.
Привлекательность совершенных нейронных сетей заключается в их сводимости к однослойным (которыми они по своей природе и являются). Более того, при применении таких передаточных функций, как 1, 2, 3, 5, не требуется корректировка порогов.
Вес всех связей (в однослойной нейросети) одинаков и равен 1/n, где n – число используемых факторов.
Кроме того, совершенная нейросеть, являющаяся однослойной, позволяет непосредственно и наглядно корректировать влияние каждого фактора на принимаемое решение. Для этого до общей корректировки весов необходимо вес соответствующей связи положить равным тому коэффициенту, с которым предполагается учет влияния данного фактора на принимаемое решение. (Таким образом реализуется понятие слабой или сильной зависимости.) После выполнения такой операции для тех весов связей, для которых это необходимо, производится общая корректировка весов. Для каждого нейрона выходного слоя она заключается в делении каждого веса на сумму весов п связей, ведущих к данному нейрону. (Фактически это приводит к применению передаточной функции 5.)
Рассматриваемый ранее достаточно универсальный пример действий контролера электропоезда, очевидно, не порождает совершенную нейросеть, хотя построенная нейросеть и сводится к однослойной.
Здесь уместен пример из лекции 3, а также модель, где действуют несколько строительных компаний, несколько субподрядных организаций и несколько заводов – изготовителей стройматериалов. В каждой ситуации обязательно представлены все участники: компания, субподрядная организация, завод-изготовитель.
Другим важным примером может служить рассматриваемая в лекции 12 система банковского мониторинга [28], в которой каждая ситуация предполагает обязательное вхождение оценок (по диапазонам изменения) всех факторов:
собственный капитал;сальдированные активы;ликвидные активы;обязательства до востребования и т.д.
Следует отметить и другие СПР на основе оценки политических, социальных и экономических факторов, а также системы управления на основе конкретных наборов или видов как возмущений, так и регулируемых параметров. Здесь везде речь идет о таблично заданных (на этапе обучения или построения нейросети) функциях многих переменных (векторов) при заданной постоянной размерности.Переменными являются оценки достоверности исследуемых факторов. Скалярным ответом является распределенное возбуждение нейронов выходного слоя, которое, в свою очередь, может указывать на вектор, компоненты которого – конкретные управляющие воздействия, параметры поведения, характеристики рынка, прогноз биржевых сделок и т.д.
Таким образом, совершенные нейронные сети, сводящиеся к однослойным, по-видимому, имеют самое широкое применение. Усилия по их разработке примитивны и не отвлекают от решения проблемы накопления опыта на практике и в науке: в торговых сделках, сомнительных инвестициях, банковских операциях, а также при моделировании сложных систем управления, исторических и социальных процессов и т.д.
Возможность применения однослойных нейросетей
Исследуем передаточную функцию 3 и использующую ее нейросеть на рис. 10.2. Анализируя прохождение сигнала по нейросети при предъявлении s-й эталонной ситуации, т.е. подавая на вход соответствующую комбинацию ns единиц, видим, что при единичных весах связей нейронов выходного слоя значение возбуждения нейрона, соответствующего решению, равно ns. Эта величина не зависит от пути прохождения возбуждения каждого рецептора, т.е. от того, сколько нейронов было на его пути. Сказывается свойство ассоциативности выбранной передаточной функции при малом значении порога. В этом случае свойство ассоциативности вырождается в свойство аддитивности, где функция от набора значений равна сумме функций от каждого значения.
Действительно, комбинация Х1 = Х3 = Х5 = Х7 = 1 приводит к величине возбуждения нейрона R1 , равной 4, значение Х10 = 1 приводит к единичному возбуждению того же нейрона, комбинация Х1 = Х6 = Х7 = 1 приводит к величине возбуждения нейрона R2 , равной 3, и т.д.
Возникает вопрос: не проще ли сформировать нейросеть, приблизив ее к табличному виду с помощью связей, непосредственно соединяющих множество тех рецепторов, которые образуют ситуации, приводящие к одному решению, с нейроном, закрепленным за этим решением?
Итак, создавая нейросеть на основе логической схемы обработки высказываний, мы заменили операции


 |
(10.3) |
Множество всех высказываний или соответствующих им рецепторов, участвующих в формировании одного решения, в лекции 3 была названа обобщенной ситуацией.
Множество {X1 , X3 , X5 , X10 } является обобщенной ситуацией, аналогично – множество {X1 , X2 , X4 , X6 , X7 , X12 , X14 } и т.д.
В сущности, это не означает, что при формировании каждого решения все нейроны-рецепторы, образующие обобщенную ситуацию, должны получать ненулевое возбуждение.
Она делит подмножество на два, каждое из которых содержит единственный элемент. Закрепляем за ними (окончательно, за соответствующими связями) значение веса 0,25, т.е. ранее найденное значение 0,5 делим поровну (рис. 10.3).
Анализ следующего подмножества приводит к аналогичному результату. Последнее подмножество содержит два элемента, объединенных в (10.2) операцией конъюнкции. За каждым из них окончательно закрепим вес связи, равный 0,5.
Рассмотрим следующую логическую функцию, приводящую к решению R2. Здесь последняя производимая операция – дизъюнкция. Она делит множество нейронов, составляющих обобщенную ситуацию, на два подмножества: {X1, X7, X4, X6} и {X2, X12, X14}. Присвоим им предварительно единичные веса связей.
Анализируя первое подмножество, находим последнюю логическую операцию – конъюнкцию, разделяющую его на два меньших подмножества {X1, X7} и {X4, X6}. Введенный ранее единичный вес делим поровну, принимая уточненные веса связей нейронов равными 0,5.
Вновь анализируем первое из сформированных множеств нейронов. Операция конъюнкции делит это подмножество на два, содержащие по одному элементу: {X1} и {X7}. Делим поровну найденный ранее вес, полагая веса соответствующих связей нейрона R2 равными 0,25.
Последней логической операцией, связывающей высказывания Х4 и Х6 второго подмножества, является дизъюнкция. Она окончательно сохраняет ранее определенный вес связей, равный 0,5.
Анализируя третье, последнее подмножество, видим, что в записи, объединяющей высказывания в (10.2), отсутствуют скобки. Это (хотя существует ранжирование логических операций при их выполнении) свидетельствует о том, что все высказывания объединяет одна операция. Так как это – конъюнкция, делим поровну предварительно найденный вес, полагая соответствующие веса связей равными 0,33.
Аналогично корректируем остальные веса связей.
Рассмотрение примера приводит к простому формальному описанию алгоритма коррекции весов связей нейронов выходного слоя однослойной нейросети, которое здесь не приводим.
В табл. 10. 3 даны результаты расчета ситуаций, отображенных в табл. 10.1 и 10.2.
Видим, что по эталонным ситуациям нейросеть "работает" правильно, что порождает доверие к ней в процессе эксплуатации. Вполне объяснимы и другие решения, совпадающие с ранее полученными.
Рассуждения об ассоциативности передаточной функции приводят к предположению о полном совпадении результатов расчетов возбуждения нейронов выходного слоя, отображенных в табл. 10.2 и табл. 10.3. Однако это не так. А именно: нахождение весов связей внесло коррективы, и результаты расчетов несущественно отличаются. Несущественность этого несовпадения определяется тем, что, во-первых, для всех эталонов совпадают принимаемые решения, во-вторых – для одинаковых ситуаций сохраняется предпочтительный ряд таких решений.
| 0 | 0 | 0 | 0,5 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 |
| 0,5 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,55 | 0,05 | 0,4 |
| 0,5 | 1 | 1 | 1 | 0 | 0,25 | 0,25 | 1,16 | 0,33 | 1,54 |
| 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,78 | 0,33 | 0,45 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Обобщенные ситуации имеют "технологическое" значение. Они объединяют нейроны-рецепторы, между которыми, с одной стороны, и нейроном выходного слоя – с другой должны быть введены связи в однослойной нейросети. Нейроны-рецепторы по-прежнему возбуждаются в соответствии с ситуациями – конъюнкциями высказываний, для которых формируется нейросеть. А оператор нейросети следит за тем, чтобы "физический смысл" явлений не пропадал, а именно – чтобы соблюдались права исчерпывающих множеств событий.
По описанию (10.3) построим однослойную нейросеть (рис. 10.3, на веса пока не обращаем внимания) и проанализируем ее работу при ситуациях, отображенных в таблицах 10.1 и 10.2.

Рис. 10.3. Однослойная нейросеть
Видим, что нейросеть в целом делает верные выводы. Взаимно-относительные оценки возбуждения нейронов выходного слоя правильно определяют ситуации, однако абсолютные значения возбуждения этих нейронов различны для различных ситуаций. Тогда, как и прежде, приведем их к отрезку [0, 1], скорректировав веса связей. Для воспроизведения структуры и взаимодействия высказываний и ситуаций придется обратиться к описанию (10.2). Определим по первой логической функции в (10.2), задающей решение R1, последнюю операцию. Это операция дизъюнкции.
Она делит множество нейронов обобщенной ситуации на два подмножества {X1, X3, X5, X7} и {X10, X13}. Закрепим предварительно за ними единичное значение весов связей.
В этом разбиении на непересекающиеся подмножества нам помогает отмеченная ранее единственность вхождения каждого выражения в запись логической функции.
Отдельно исследуем сформированные подмножества.
По первому из них находим последнюю выполняемую логическую операцию. Это операция конъюнкции, разбивающая подмножество на два меньших: {X1, X7} и {X3, X5}. Закрепим за каждым из них значение веса 0,5 (ранее найденную единицу делим поровну).
Вновь, начиная с первого, анализируем последовательность трех подмножеств. Последняя операция, производимая над элементами первого подмножества, является конъюнкцией.
Она делит подмножество на два, каждое из которых содержит единственный элемент. Закрепляем за ними (окончательно, за соответствующими связями) значение веса 0,25, т.е. ранее найденное значение 0,5 делим поровну (рис. 10.3).
Анализ следующего подмножества приводит к аналогичному результату. Последнее подмножество содержит два элемента, объединенных в (10.2) операцией конъюнкции. За каждым из них окончательно закрепим вес связи, равный 0,5.
Рассмотрим следующую логическую функцию, приводящую к решению R2. Здесь последняя производимая операция – дизъюнкция. Она делит множество нейронов, составляющих обобщенную ситуацию, на два подмножества: {X1, X7, X4, X6} и {X2, X12, X14}. Присвоим им предварительно единичные веса связей.
Анализируя первое подмножество, находим последнюю логическую операцию – конъюнкцию, разделяющую его на два меньших подмножества {X1, X7} и {X4, X6}. Введенный ранее единичный вес делим поровну, принимая уточненные веса связей нейронов равными 0,5.
Вновь анализируем первое из сформированных множеств нейронов. Операция конъюнкции делит это подмножество на два, содержащие по одному элементу: {X1} и {X7}. Делим поровну найденный ранее вес, полагая веса соответствующих связей нейрона R2 равными 0,25.
Последней логической операцией, связывающей высказывания Х4 и Х6 второго подмножества, является дизъюнкция. Она окончательно сохраняет ранее определенный вес связей, равный 0,5.
Анализируя третье, последнее подмножество, видим, что в записи, объединяющей высказывания в (10.2), отсутствуют скобки. Это (хотя существует ранжирование логических операций при их выполнении) свидетельствует о том, что все высказывания объединяет одна операция. Так как это – конъюнкция, делим поровну предварительно найденный вес, полагая соответствующие веса связей равными 0,33.
Аналогично корректируем остальные веса связей.
Рассмотрение примера приводит к простому формальному описанию алгоритма коррекции весов связей нейронов выходного слоя однослойной нейросети, которое здесь не приводим.
В табл. 10. 3 даны результаты расчета ситуаций, отображенных в табл. 10.1 и 10.2.
Видим, что по эталонным ситуациям нейросеть "работает" правильно, что порождает доверие к ней в процессе эксплуатации. Вполне объяснимы и другие решения, совпадающие с ранее полученными.
Рассуждения об ассоциативности передаточной функции приводят к предположению о полном совпадении результатов расчетов возбуждения нейронов выходного слоя, отображенных в табл. 10.2 и табл. 10.3. Однако это не так. А именно: нахождение весов связей внесло коррективы, и результаты расчетов несущественно отличаются. Несущественность этого несовпадения определяется тем, что, во-первых, для всех эталонов совпадают принимаемые решения, во-вторых – для одинаковых ситуаций сохраняется предпочтительный ряд таких решений.
| 0 | 0 | 0 | 0,5 | 0 | 0 | 1 | 0,55 | 0,95 | 0,25 |
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 1 | 0,5 | 0,55 | 0,8 | 0,65 |
| 0,5 | 0,5 | 0,5 | 0 | 1 | 0,5 | 0 | 0,55 | 0,05 | 0,4 |
| 0,5 | 1 | 1 | 1 | 0 | 0,25 | 0,25 | 1,16 | 0,33 | 1,54 |
| 1 | 0,5 | 0,5 | 0 | 0,5 | 0,25 | 0,5 | 0,78 | 0,33 | 0,45 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0,6 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0,4 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0,3 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0,1 | 0 | 0,3 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0,9 | 0 | 0,3 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,5 | 0 | 0,5 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0,2 | 0 | 0,5 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0,8 | 0 | 0,5 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0,1 | 0,9 | 0,5 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0,9 | 0,1 | 0,5 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Однако всегда ли можно так упростить задачу создания СПР, сведя ее к получению однослойной нейросети? В разделе 9.1 показано, что это не всегда возможно. Там приведена попытка воспроизведения логического описания СПР
 | (10.4) |
Однако дело не столь безнадежно. Рассмотрим обобщенные эталоны, определяющие каждое решение:
 | (10.5) |
Изменим логическое описание, "размножив" одинаковые решения так, чтобы ни один обобщенный эталон не оказался включенным в другой. Для этого введем условно два одинаковых решения R11 = R12 = R1.
Представим систему (9.6) в виде
 | (10.6) |

Рис. 10.4. Нейросеть, построенная по описанию (10.6)
Легко видеть, что в ней отсутствует побочный эффект, т.е. корректировка порогов не требуется.
Таким образом, для применения однослойных нейросетей необходимо (достаточно ли?), чтобы обобщенная ситуация, соответствующая одному решению, не поглощала все нейроны, которые образуют некоторую ситуацию, ведущую к другому решению.
Так, если не была бы найдена логическая ошибка, в результате чего ситуация Х10 в (9.1) не сменилась ситуацией Х10

в (10.1)-(10.2), обобщенные ситуации, ведущие к решениям R3 и R4, поглотили бы эту ситуацию. Это значит, что при задании эталона Х8 = Х10 = 1 единичное значение возбуждения получали бы нейроны R1 и R3. Аналогично, предъявление эталона Х9 = Х10 = 1 привело бы к единичному значению возбуждения нейронов R1 и R4.